JUMP TO TOPIC
Algebra|Definition & Meaning
Definition
Algebra is a field of mathematics that aids in the depiction of problems or situations using mathematical expressions. It involves both unknown values called variables that we can find and known values called constants.
To construct a meaningful mathematical expression, variables such as x, y, and z,
are combined with arithmetic operations such as multiplication, subtraction, addition, and division.
Algebra is the branch of mathematics concerned with symbols and their manipulation rules. In elementary algebra, these symbols (now expressed as Latin and Greek letters) indicate variables, which are quantities without set values. Equations in algebra express the relationships between variables, just as sentences describe the relationships between individual words.
The following figure represents the basic graph of a natural graph.
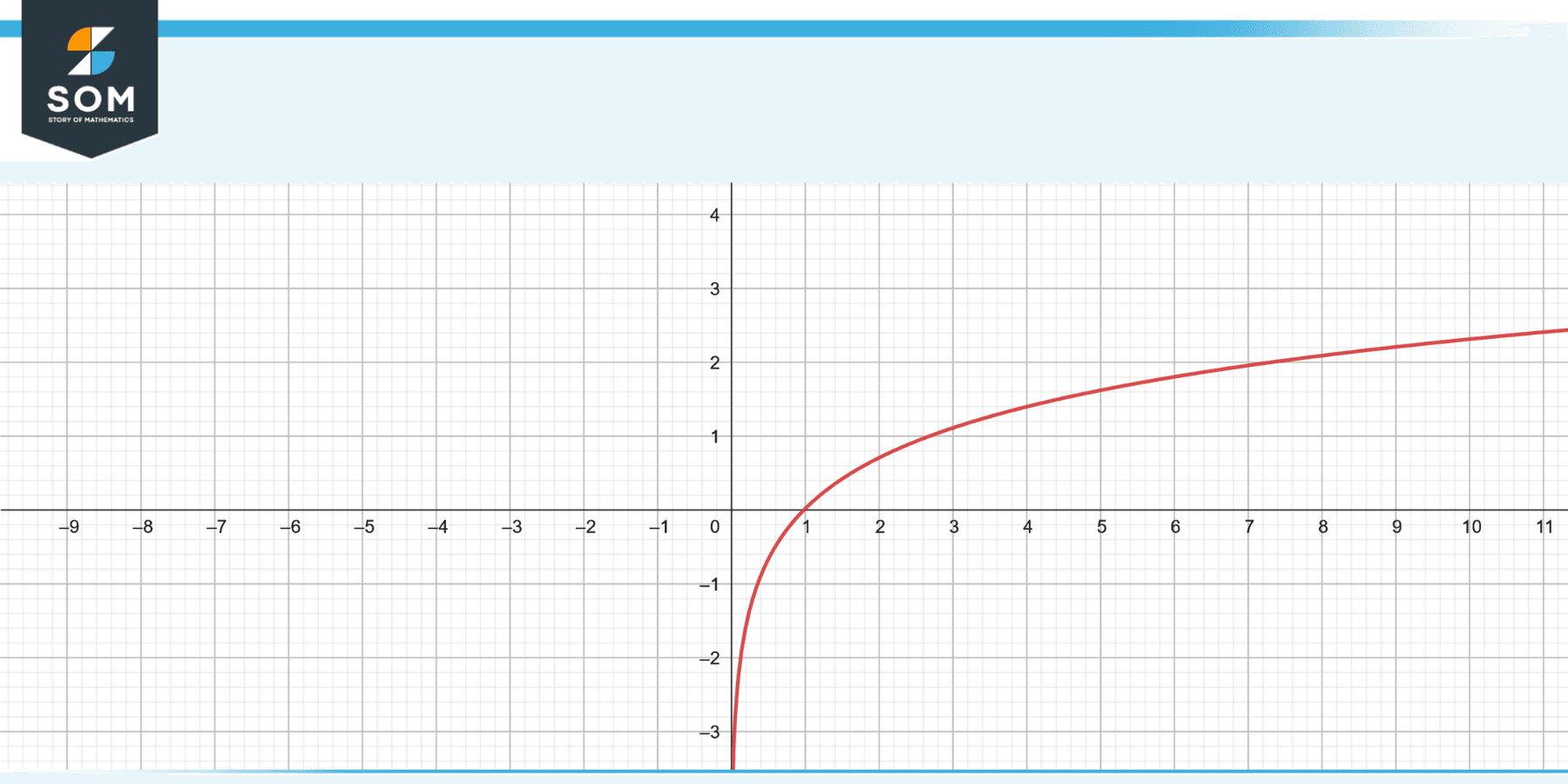
Figure 1 – Algebraic graph of a natural log.
What Is Algebra in Mathematics?
The study of algebra is a sub-field of mathematics that focuses on symbols and the mathematical operations that can be performed across them. These symbols, which are referred to as variables, don’t have any consistent values associated with them. When we look at the challenges that we face in real life, we frequently see some values that are always shifting. However, there is an ongoing requirement to portray these ever-evolving ideals.
In the context of algebra, such values are frequently denoted by characters such as x, y, z, p, or q; the term “variable” refers to the fact that these symbols are used to represent the values. In addition, in order to determine the values, these symbols are subjected to a variety of arithmetic operations, including addition, subtraction, multiplication, as well as division.
Illustration of tangent is shown below.
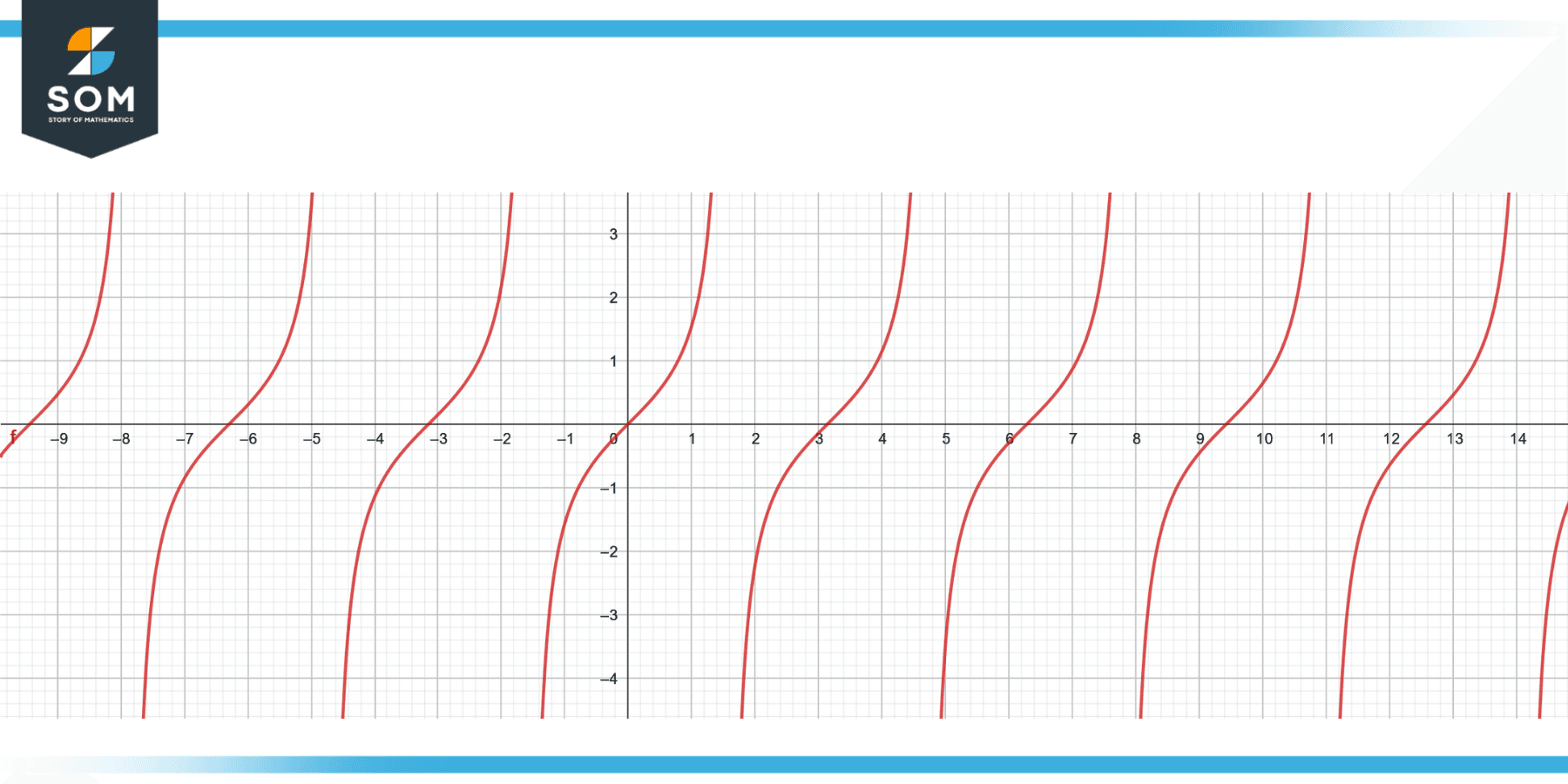
Figure 2 – Algebraic graph of tangent.
The graph below shows the graph of cos.
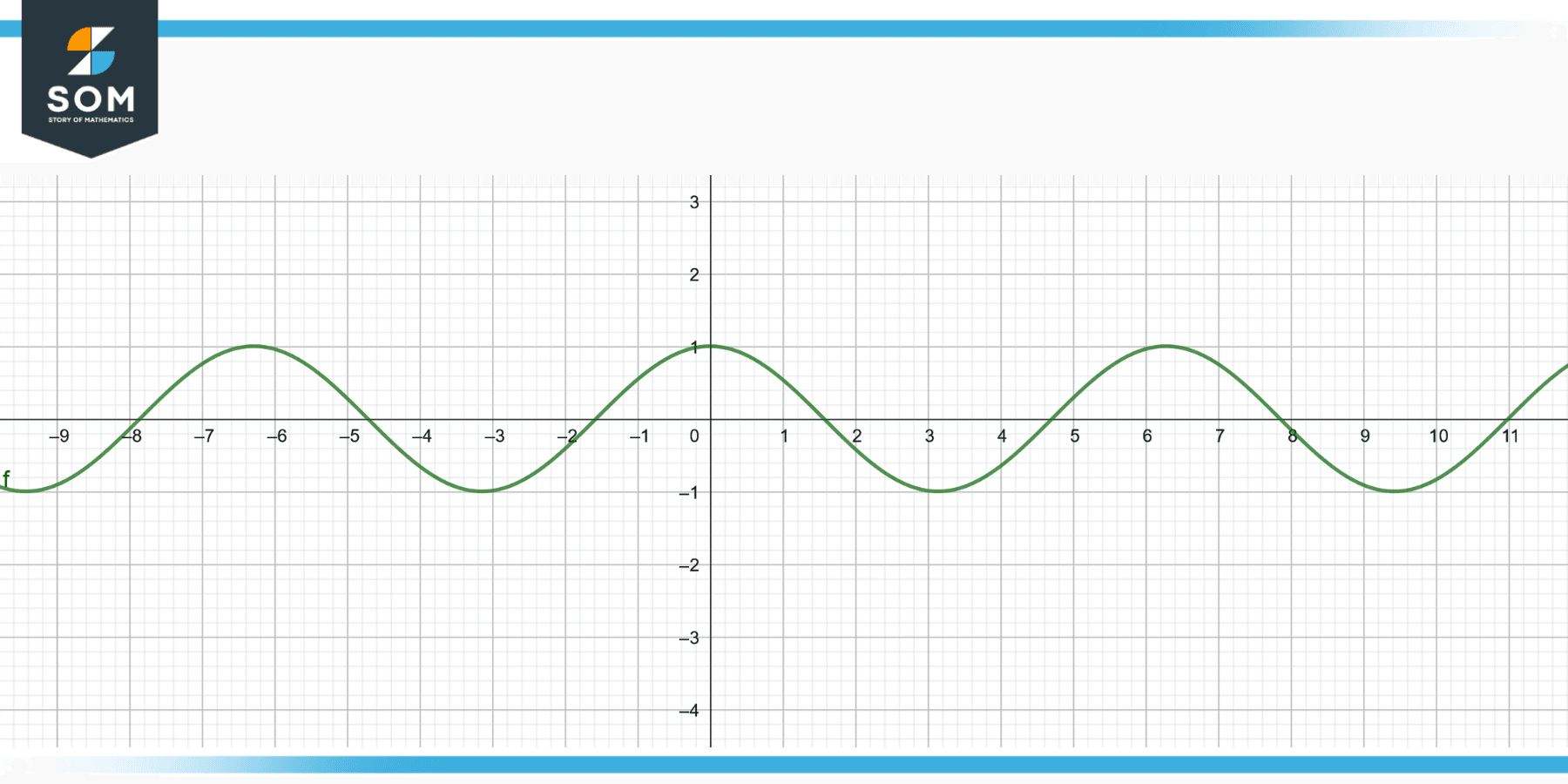
Figure 3 – Algebraic graph of cosine.
The Different Algebraic Branches
Utilizing a wide variety of different algebraic expressions is one way that the difficulty of algebra can be reduced. The study of algebra can be broken down into a number of sub-fields, which are described in the following order of increasing application and level of difficulty:
- Pre-algebra
- Elementary Algebra
- Abstract Algebra
- Universal Algebra
Pre-algebra
Mathematical expressions can be created with the assistance of fundamental methods for presenting unknowable values as variables. It aids in the process of translating situations from real life into mathematical expressions using algebraic notation. In pre-algebra, one of the tasks consists of formulating a mathematical equation of the problem statement that has been presented.
Elementary Algebra
The primary focus of elementary algebra is on finding valid solutions to algebraic expressions by solving them. In elementary algebra, more straightforward variables like x and y are each given their own equation to represent them. These equations are referred to as linear equations, quadratic equations, and polynomials, respectively, depending on the degree of a variable.
Abstract Algebra
In abstract algebra, rather than focusing on straightforward mathematical number systems, the focus is on more conceptually rich topics such as groups, rings, and vectors. By expressing the addition & multiplication characteristics together, one can quickly reach a simple abstraction level known as rings.
The concepts of group theory & ring theory are both significant in the field of abstract algebra. The fields of computer science, physics, and astronomy all make extensive use of abstract algebra, which represents quantities through the utilization of vector spaces.
Universal Algebra
The term “universal algebra” refers to a type of algebra that can be applied to all the other types of mathematics, including trigonometry, calculus, and coordinate geometry, that involve algebraic expressions. In each of these sub-fields, the study of universal algebra focuses on mathematical expressions & does not include an investigation of algebraic models.
Universal algebra can be thought of as the overarching umbrella under which all other sub-fields of algebra fall. Any one of the issues that arise in real life may be placed in any one of the sub-fields of mathematics, and abstract algebra can be used to find a solution to any of those issues.
Geometry and Algebra
We examine geometric objects including their variety that are described by polynomial equations in algebraic geometry. The most commonly studied classes of algebraic curves include lines, circles, parabolic arcs, ellipses, and hyperbolas. Algebraic geometry can indeed be utilized to examine the dynamical characteristics of robotics mechanisms in the real world.
A robot has an endless range of possible actions & states and can navigate in continuous space. Whenever the robot has moving arms and legs, the search space expands to include many dimensions. Robot kinematics can be expressed as a system of polynomial equations that can be resolved with the use of algebraic geometry techniques.
In addition, geometric modeling, control theory, and statistics all make extensive use of algebraic geometry. Integer programming, graph matching, game theory, and string theory are also related.
Computer Programming With Algebra
Mathematical languages bring together various disciplines, including science, technology, and engineering. That is why someone who is interested in computer coding and programming should learn how to understand and use mathematical logic.
A strong understanding of algebra includes defining the relationships between items, developing analytical skills to aid in decision-making, and critical thinking with constrained circumstances.
Inference techniques used within knowledge engineering are one example of how algebra is employed in this way. Symbols for variables and constants are used to represent things in the actual world.
The inference technique determines how to use the facts to solve the problem once the knowledge engineer provides a set of facts and describes what is true.
Furthermore, knowledge bases can indeed be reused for numerous projects without change, as truth is true despite what task one is attempting to solve.
The Use of Algebra in Everyday Life
In the world that we actually live in, there are a great many situations that call for the use of algebra. Its usefulness is currently being quantified on a global scale in every aspect of our life. Take, for instance, the realm of shopping as an example. In this scenario, we need to adhere to a certain budget with the products in the basket, as well as some algebraic formulation must be applied.
Algebra is utilized by economists in order to find solutions to issues that are associated with debts or loans, and this analysis is performed for each and every nation’s economy.
In everyday life, mathematics can be compared to something like universally handy equipment or a magic wand that can help one deal with the day-to-day challenges that come up in life.
Algebra is typically the most effective strategy to employ whenever you are faced with a mathematical challenge, such as when you are tasked with resolving an equation or determining the solution to a geometrical problem.
A Numerical Example of Algebra
Example
Ali was carrying a few chocolates in his bag. Jack happened to be there and helped himself to five of the chocolates. Then there were only seven chocolates left in his possession altogether. When Razi came to him, did he eat all of those chocolates?
Solution
Let’s say Razi stole five of Ali’s chocolates, leaving him with x chocolates.
x − 5 = 7
Therefore, we take x and deduct five from it. In addition to this, after everything was said and done, Ali was given seven chocolates.
x − 5 + 5 = 7 + 5
x = 12
All mathematical drawings and images were created with GeoGebra.
