Alternate Interior Angles|Definition & Meaning

What Are Alternate Interior Angles? 

The pair of angles generated when a transversal intersects two parallel lines are referred to as alternate interior angles. These angles are generated on the inner side of the line segments but on different sides of the transversal. These angles are invariably equal. One more interpretation is possible with this piece of information.

The various interior alternative angles can be used to demonstrate whether or not the supplied lines are parallel. If these angles are the same, then the lines given and intersected by a transversal are said to be parallel.

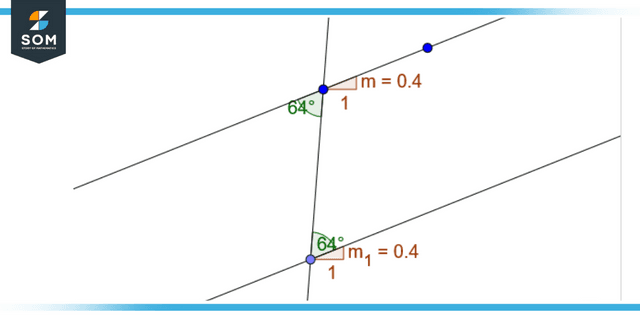
Figure 1: Representation of alternate interior angles.

The Converse of the Theorem Regarding Alternate Interior Angles

Suppose a transversal intersects two lines to equal the alternate interior angles. In that case, the two lines are considered to be parallel by the converse of the alternate interior angles theorem.

Let us better understand this with the assumption, which demonstrates that 1 = 5 (similar angles) and 3 = 5 (vertically opposite angles). Thus, ∠1 = ∠3. In a similar vein, we can demonstrate that 2 equals 4. This demonstrates that the two given lines are indeed parallel because the alternate interior angles in both lines are equal.

Identifying Alternate Interior Angles

A transversal is defined as a line that goes through the middle of another line. Alternate interior angles are angles within the boundaries of the 2 lines but on opposite sides of the transversal. These angles are also known as alternate inside angles.

If the two l lines are parallel to one another, then the interior angles of the alternate configurations will be congruent.

• If two lines are parallel, then the angles formed by those lines must be corresponding. Alternate interior and alternate exterior angles must also be congruent.
• If two lines are parallel, the interior angles on the same side are complementary, and the exterior angles on the same side are

Difference Between Alternate Interior and Alternate Exterior Angle

The angles within the space between the parallel lines, such as angles 2 and 8, are referred to as internal angles. In contrast, the angle on the exterior of the two parallel lines, such as angles 1 and 6, are referred to as exterior angles. Angles on different sides of the transversal are referred to as alternate angles. For example, 1 plus 8 is an alternate angle.

Co-interior Angles

The two angles that are located on the same side of the transversal are the ones that are referred to as co-interior angles or consecutive interior angles. The interior angles, which are also known as co-internal angles, add up to a total of 180 degrees. That adding the two interior angles along a transversal is additional is the implication of this statement.

The co-interior angles have a shape similar to a “C,” and the angles are not the same relative to one another. There are a few names for the co-interior angle, including the consecutive interior angles and the same side interior angles.

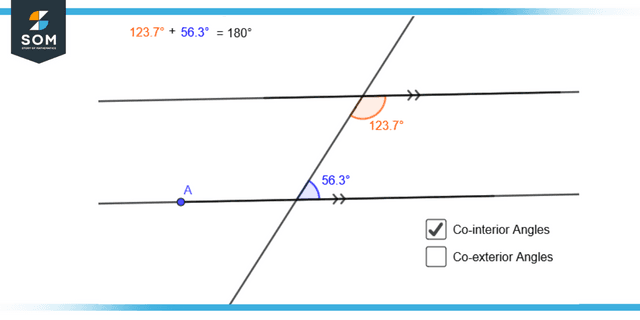
Figure 2: Representation of Co-interior angles.

Properties

• These two angles are identical to one another.
• The total angles obtained on the side same as the transversal inside the 2 parallel lines, is always equal to 180 degrees. This is because these angles are formed on the same transversal side.
• Regarding lines that aren’t parallel, alternate interior angles don’t have any particular characteristics to look out for.

Important Points To Remember

• The vertices of consecutive interior angles, also known as co-interior angles, can be different, but they always fall on the identical side of the transversal.
• These angles can be found in the space between two lines.
• Consecutive interior angles are not next to one another.
• When a transversal is placed on two parallel lines, the sum of the generated co-interior angles will always add up to 180 degrees if the transversal is drawn on both lines.
• It is always the case that the sum of a parallelogram’s consecutive inner angles is

Theorem and Proof Statement

The theorem asserts that “if a transversal intersects the set of parallel lines, then the alternate interior angles are congruent.” The proof statement demonstrates that this is indeed the case.

Given: a/d

In order to demonstrate: ∠3 = ∠6 and ∠4 = ∠5

Assuming that a and g are two parallel lines and that l is a transversal that cuts across both a and d at points P and Q, here’s how you can prove it:

Because parallel lines have certain qualities, we know that if a transversal cuts through any two of them, the angles that are equivalent to each other and those that are vertically opposing will be identical. Therefore:

∠2 = ∠5………..(i) [corresponding angles]

∠2 = ∠4………..(ii) [angles that are vertically opposite one another]

From equations (i) and (ii), we get:

∠4 = ∠5  [alternate interior angles]

Similarly, we can show that:

∠3 = ∠6

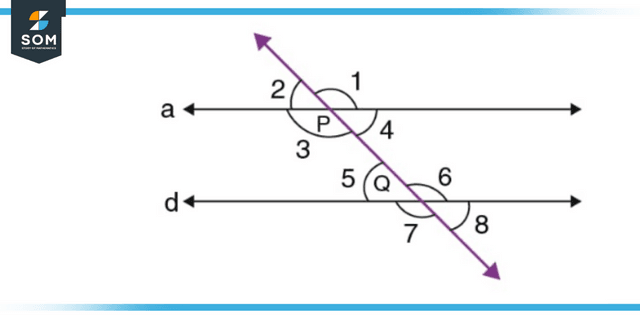
Figure 3: Representation of given theorem

Solved Examples Involving Alternate Interior Angles

Example 1

Consider a transverse intersecting two parallel lines, A and B. The point where it intersects line A is at angle 85 and the point where it intersects point B is unknown. Determine the angle at which the transverse is intersecting point B.

Solution

Finding the angle by using the property of parallel lines cutting by a transversal. Using alternate interior angle property to find the unknown angle:

B + 85 = 180

B = 180 – 85

B = 95

The unknown angle where the transversal intersects line B is equal to 95.

Example 2

What is the exterior angle of a triangle if the opposite interior angles to that exterior angle are 59 and 51?

Solution

The exterior angle will be equal to the sum of the interior angles opposite to it.

Suppose the exterior angle is x:

x = 59 + 51

x = 110

All images/graphs are created using GeoGebra.

Algorithm Definition < Glossary Index > Altitude Geometry Definiton