JUMP TO TOPIC
Altitude (Geometry)|Definition & Meaning
Definition
In mathematics (geometry to be specific), altitude is the perpendicular line segment connecting a vertex of a triangle to a point on its opposite facing side at right angle. A triangle has three altitudes. The concept is not limited to triangles only, it can be extended to any shape with odd number of vertices.
In more general terms, altitude means straight line distance (or displacement) of a point on an object standing on the ground or an object flying in the air, such that the line is perpendicular to the horizon.
Visual Illustrations of Altitude in Triangles
Following figures illustrate the concept of altitude for different types of triangles. Figure 1 shows the altitude of a right triangle.
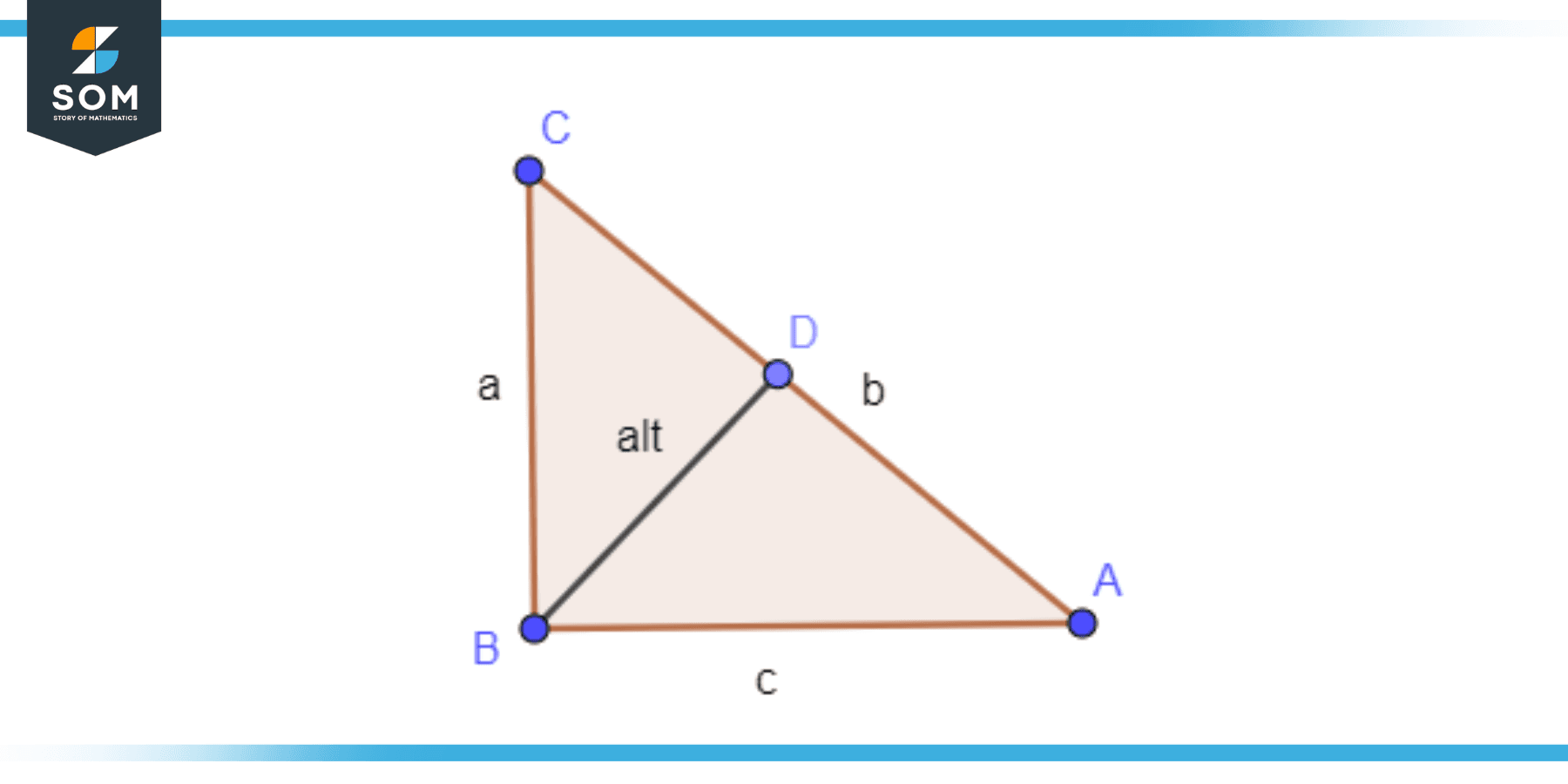
Figure 1: Altitude of Right Angled Triangle
A right angled triangle is such a triangle for which one of the angles is equal to 90 degrees (called the right angle). Its sides are termed as base (b), hypotenuse (hyp) and perpendicular (perp). The altitude of such a triangle can be calculated using the following formula:
\[ Altitude \ = \ \sqrt{ (CD)(DA) } \]
Where CD and DA are line segments. Figure 2 shows the altitude of a Equilateral triangle. An equilateral triangle is such a triangle for which all three angles or three sides are equal.
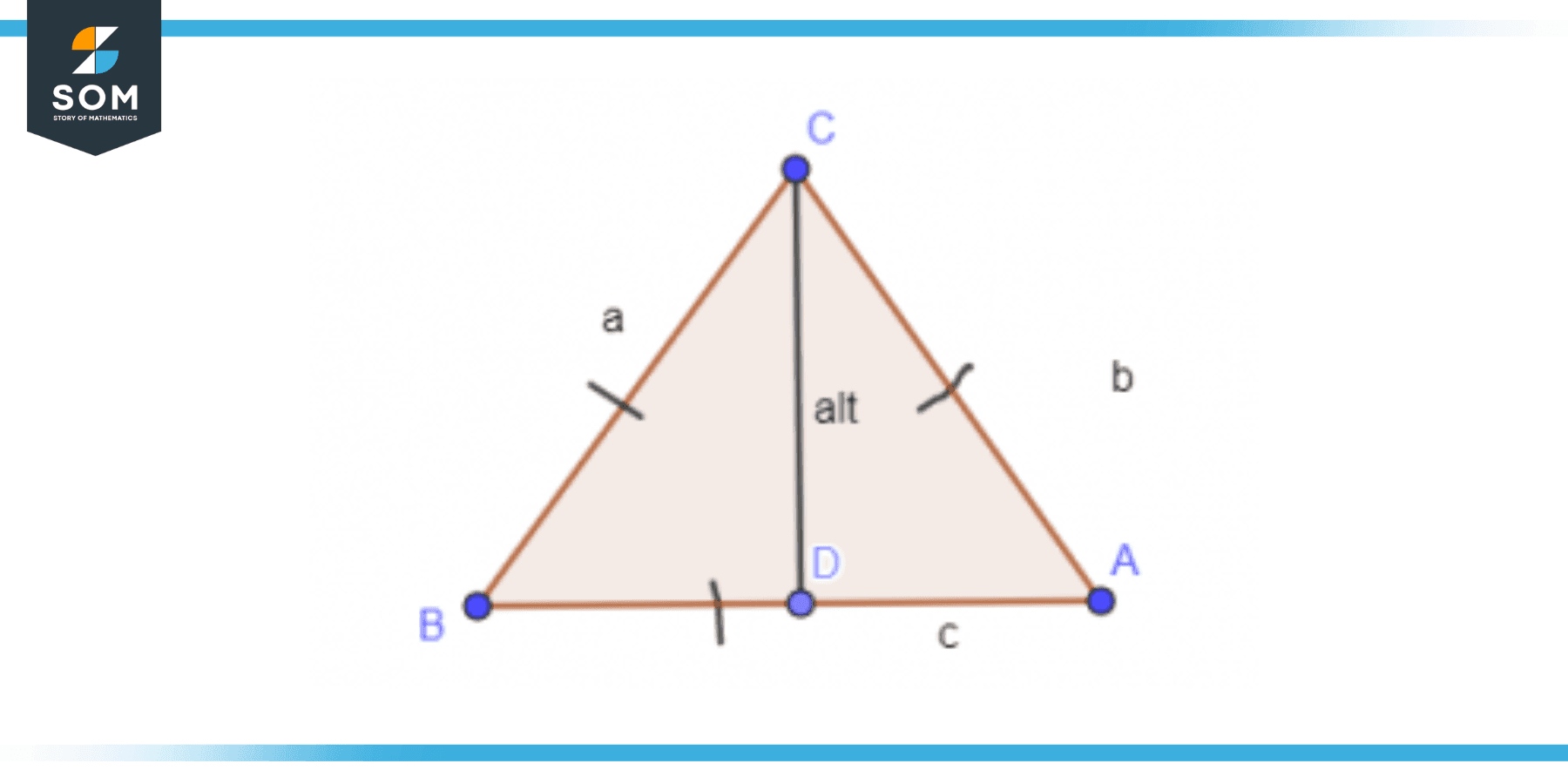
Figure 2: Altitude of Equilateral Triangle
The altitude of such a triangle can be calculated using the following formula:
\[ \text{Altitude} \ = \ \dfrac{ \sqrt{ 3 } }{ 2 } ( \text{ length of any side } ) \]
Figure 3 shows the altitude of an Isosceles triangle. An Isosceles triangle is one whose two angles or two sides are equal.
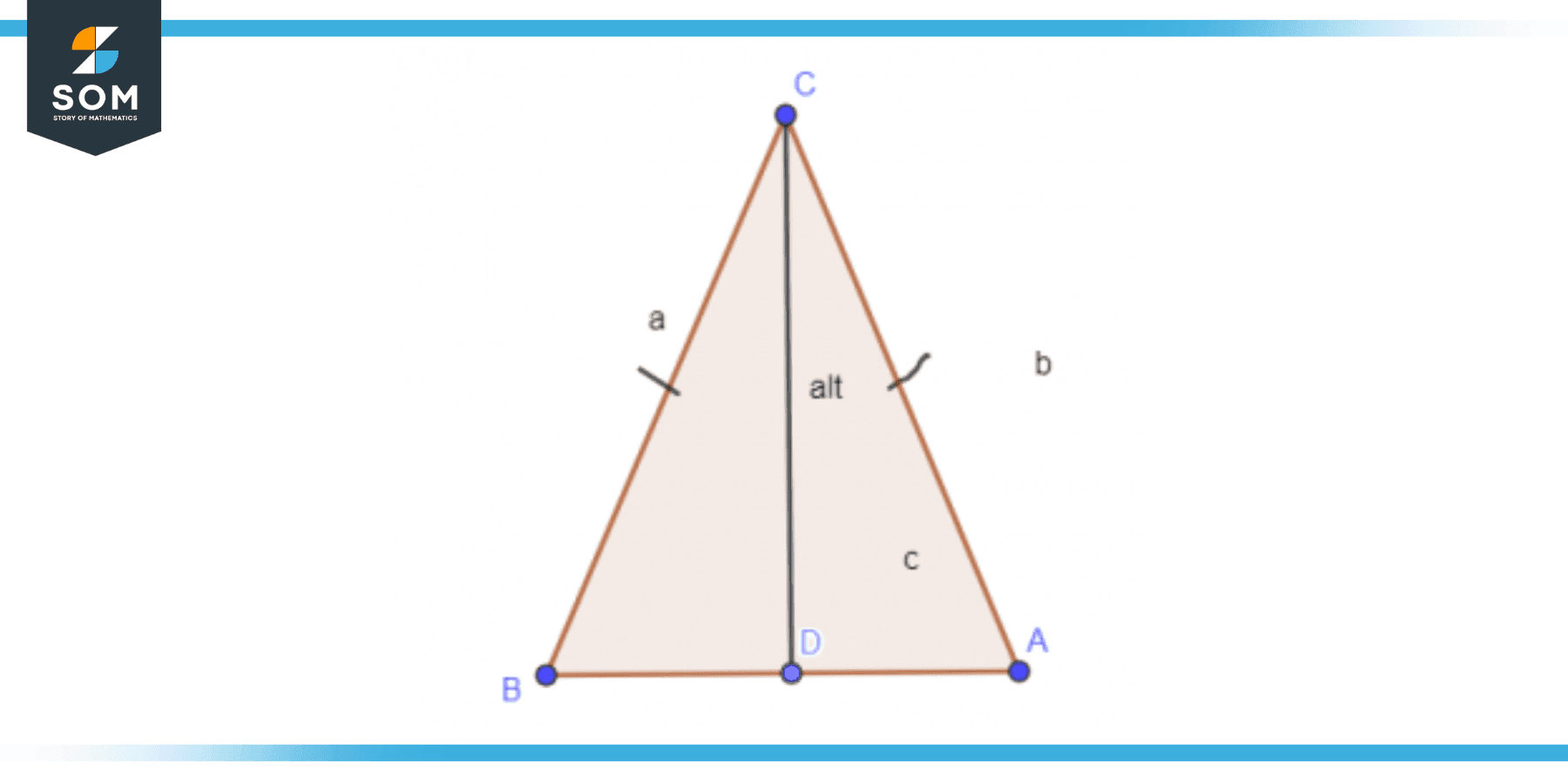
Figure 3: Altitude of Isosceles Triangle
The altitude of such a triangle can be calculated using the following formula:
\[ \text{Altitude} \ = \ \sqrt{ a^2 \ – \ \dfrac{ 1 }{ 4 } b^2 }\]
Where a is the length of any of the sides that are equal while b is the length of the third side. Figure 3 shows the altitude of a Scalene type of triangle. A Scalene triangle is such a triangle for which all angles and sides are unique and none is equal.
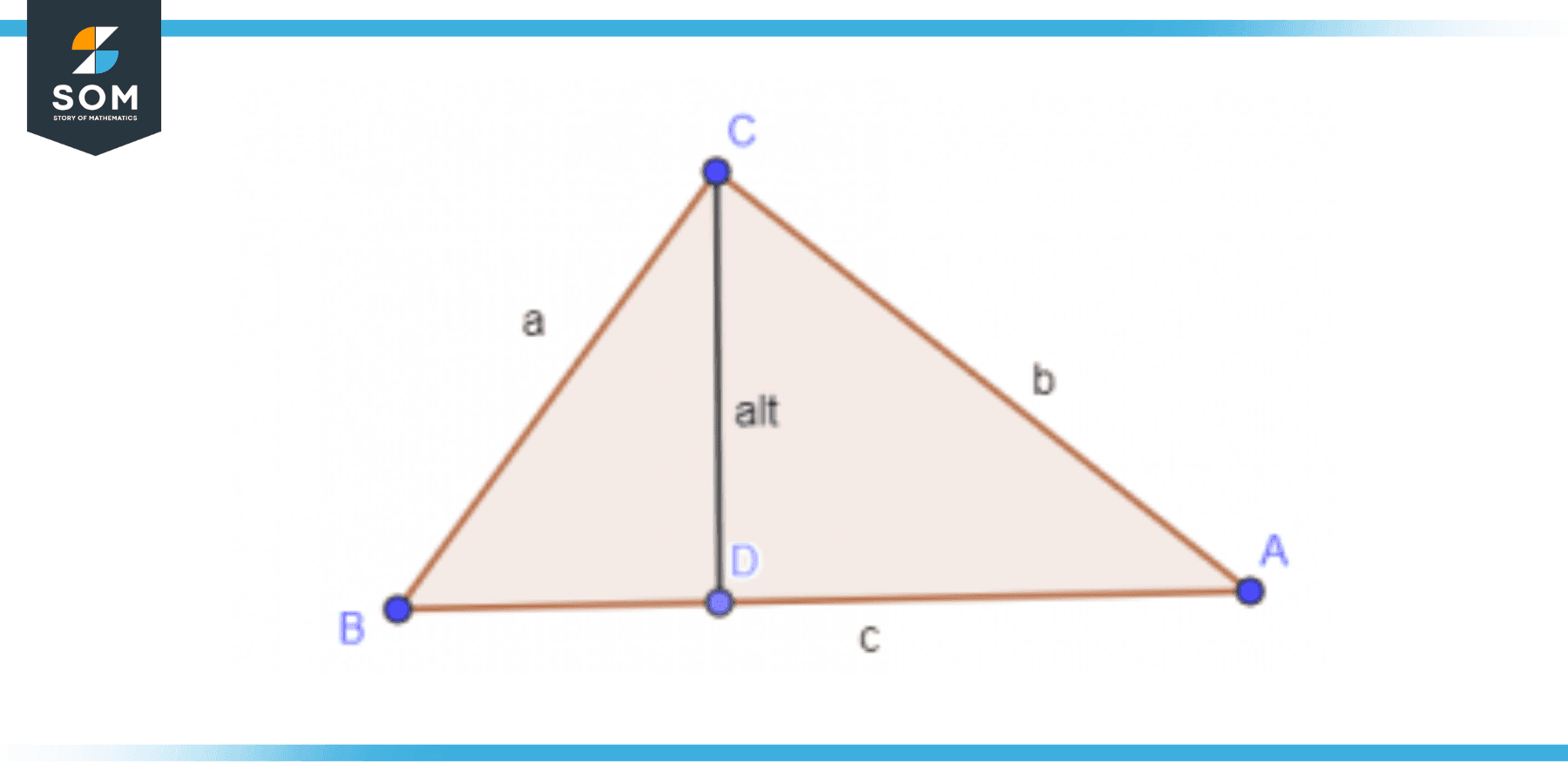
Figure 4: Altitude of Scalene Triangle
The altitude of such a triangle can be calculated using the following formula:
\[ \text{Altitude} \ = \ \dfrac{ 2 \sqrt{ s (s-a) (s-b) (s-c) } }{ b } \]
Where a, b & c are the lengths of sides, s is the semi perimeter and b is the side for which altitude is being calculated. Semi perimeter is defined as:
\[ s \ = \ \dfrac{ a + b + c }{ 2 } \]
Significance of Altitude (Geometry)
A perpendicular line drawn from a triangle’s vertex to its opposite side is called the altitude of a triangle. Since a triangle has three sides, it may be drawn along with a maximum of three altitudes .
There are several types of applications of altitudes in the geometrical problems related to triangles. The chief application among all is that the area of a triangle is calculated using the altitude, also known as height, of the triangle, which is usually represented by the letter symbol ‘h’.
Since a triangle’s height is determined by drawing a perpendicular line from its vertex to its opposite side, the altitude term is sometimes analogously referred to as the triangle’s height, especially since it forms a right-angle triangle with the base.
The altitude is a very important parameter when we talk about triangles in geometry. They help us in proving many essential laws of geometry. The term is widely used in many other domains of mathematics and physics but we will restrict our focus on the term in geometry domain.
Different Forms of Altitudes in Geometry Perspective
Altitudes have different mathematical perspectives for different types of triangles. Some of the key properties of altitudes are listed below:
a. A triangle can have a maximum of three altitudes (one per side).
b. The altitude may intersect the opposing side inside or outside the triangle depending upon the type of triangle under observation.
c. By definition, the altitude always creates a 90° angle with the side directly across from it.
There is another important term that comes across the reader whenever we are using altitudes in numerical problems. The term is called orthocenter. In the context of triangles, an orthocenter is the location where the triangle’s three elevations connect. In other words, the point of intersection of all three altitudes of a triangle is called its orthocenter.
The numerical calculation of the altitude length highly depends on the type of triangle. The formulae are listed in the next section. Let us consider four types of triangles: the Right Triangle, Equilateral Triangle, Isosceles Triangle, and Scalene Triangle.
Numerical Examples for Calculating Altitudes
The mathematical process of evaluating altitude of a triangle problems is explained with the help of numerical examples in this section. Here we suppose that we wanted to calculate the results of following operations:
(a) Find the length of altitude of a right triangle if it splits the hypotenuse line segment into two parts of lengths 3 and 4.
(b) Find the length of altitude of an equilateral triangle if the length of each side is equal to 10.
(c) Find the length of altitude of an isosceles triangle if the length of two sides is equal to 10 and the third side is 4.
(d) Find the length of altitude of a Scalene triangle if the length of its sides is 7, 8 and 9.
Solutions
(a) Right Triangle
Given that CD = 3 and DA = 4, we can use the formula:
\[ \text{Altitude} \ = \ \sqrt{ ( 3 ) ( 4 ) } \ = \ \sqrt{ 12 } \]
(b) Equilateral Triangle
Given that a = b = c = 10, we can use the formula:
\[ \text{Altitude} \ = \ \dfrac{ \sqrt{ 3 } }{ 2 } ( 10 ) \ = \ 5 \sqrt{ 3 } \]
(c) Isosceles Triangle
Given that a = 10 and b = 4, we can use the formula:
\[ \text{Altitude} \ = \ \sqrt{ (10)^2 \ – \ \dfrac{ 1 }{ 4 } (4)^2 } \ = \ \sqrt{ 100 \ – \ 4 } \ = \ \sqrt{ 96 } \]
(d) Scalene Triangle
Given that a = 7, b = 8 and c = 9, we can use the formula:
\[ s \ = \ \dfrac{ 7 + 8 + 9 }{ 2 } \ = \ \dfrac{ 24 }{ 2 } \ = \ 12 \]
Once we have semi perimeter, we can find the altitude with the following formula:
\[ \text{Altitude} \ = \ \dfrac{ 2 \sqrt{ 12 ( 12 – 7 ) ( 12 – 8 ) ( 12 – 9 ) } }{ 8 } \]
\[ \text{Altitude} \ = \ \dfrac{ 2 \sqrt{ 12 ( 5 ) ( 4 ) ( 3 ) } }{ 8 } \ = \ 6.8 \]
All mathematical drawings and images were created with GeoGebra.
