JUMP TO TOPIC
Array|Definition & Meaning
Definition
A structured arrangement of different items or things following a definite pattern or flow is known as an array. The things and items could be arithmetic numbers, any object, or pictures while the definite pattern could be columns or rows. The basic aim of arrays is to demonstrate the concept of multiplication and division and assist in counting the items.
By using arrays, multiplication and division relationships can be broken down fascinatingly. Because multiplication and division are opposites of each other, arrays illustrate this concept of inverse operations. An array can be used to quickly analyze data and easily multiply or divide groups of objects. Many examples of arrays are found in everyday life that illustrates the utility of these tools.
Condition For Pattern Arrangement in an Array
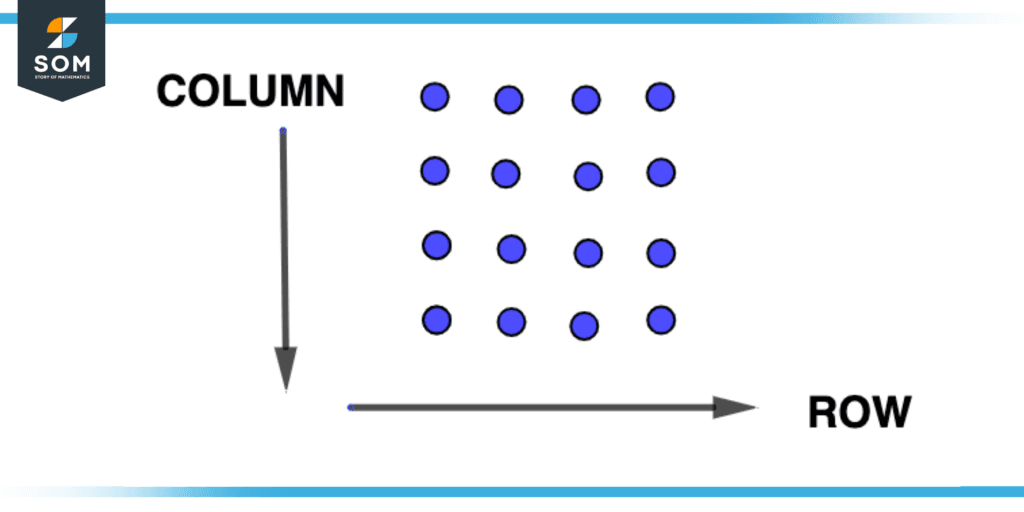
Figure 1 – Array Structure
Consider the figure shown above, the arrow starting from top to bottom shows the column arrangement while the arrow starting from left to right shows the row arrangement of the array. Anything like numbers or objects arranged in a such manner makes an array.
Rectangular Array
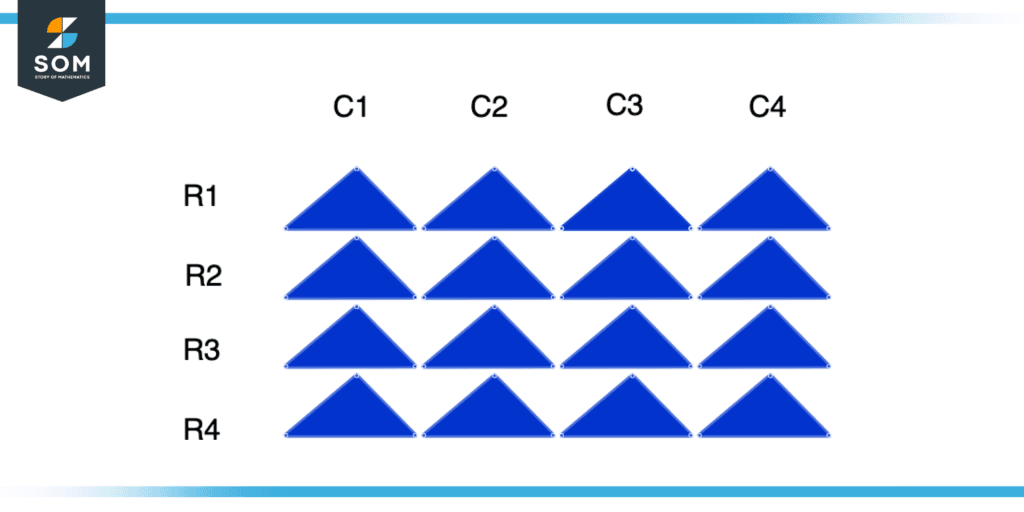
Figure 2 – Four by-Four Rectangular Array
When the number of rows and number of columns is equal in the count then it forms a rectangular array. Consider the above figure when we count the number of rows and columns, we are getting 4, so there are 4 rows and 4 columns forming a rectangular array.
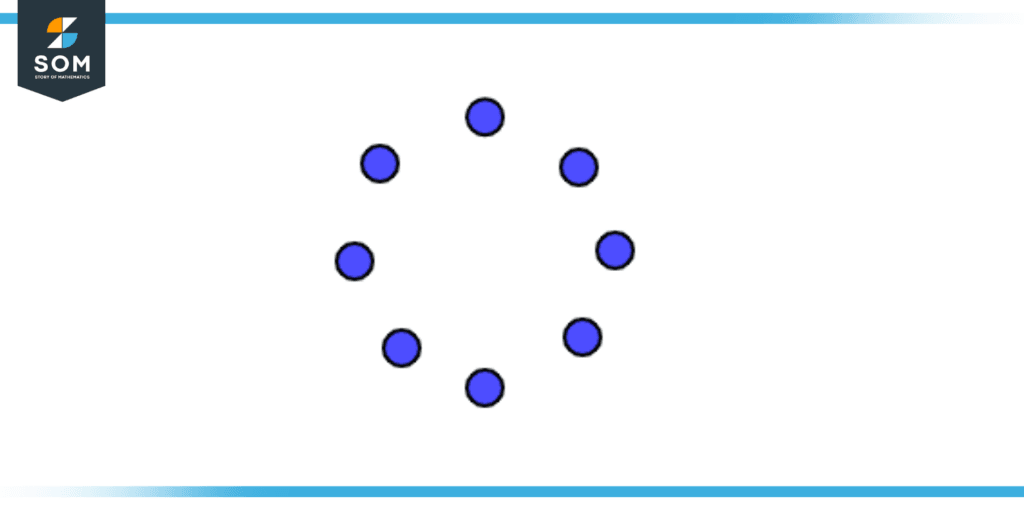
Figure 3 – Not an Array
Consider the above figure that is not an array because there is no row or column in the figure, so we can’t say this is an array.
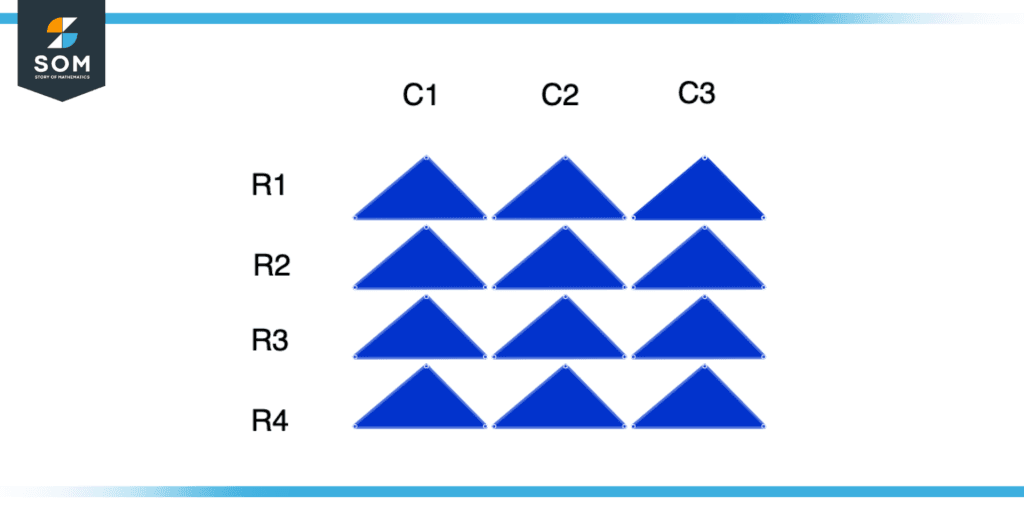
Figure 4 – Array of Four by Three
This figure has 4 rows and 3 columns, so this is a 4 by 3 array.
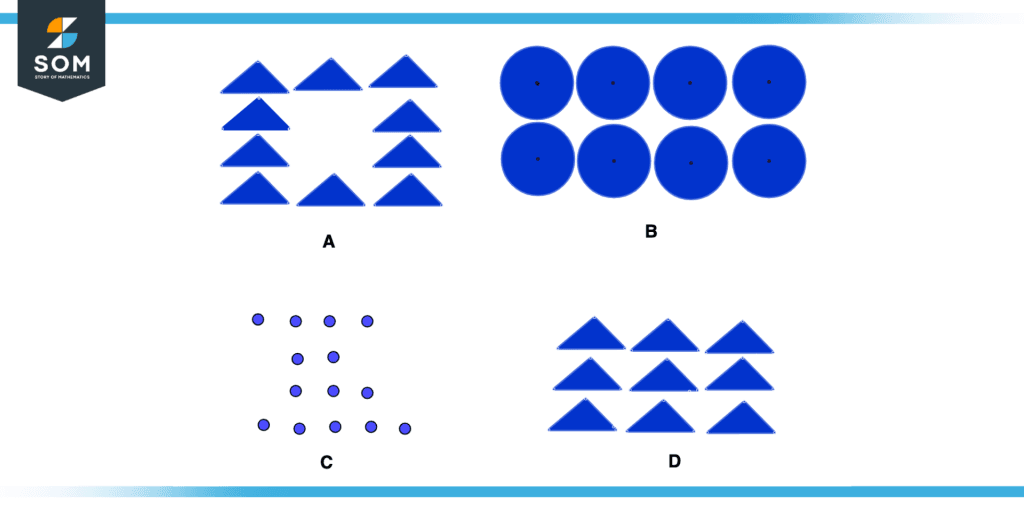
Figure 5 – Rectangular Array Worksheet
Considering the above example, we want to see if the above figures are rectangular arrays or not.
In figure A, there are three triangles in the first row and the second and third row has two triangles, so this is not an array because the array has not the same number of items in every row.
In figure B there are two rows and four columns, although it is an array it is not satisfying the condition for a rectangular array i.e., an equal number of rows and columns.
In figure C the first row has four circles, the second row has two circles, the third row has three circles, and the fourth row has five circles so there is no equal number of items in each row, so it is neither an array nor a rectangular array.
In figure D the number of rows and columns is three, so it is a rectangular array.
Demonstrating Multiplication using Array
Multiplication is commonly explained with arrays by referring to the factors being multiplied. An array of sixteen oranges arranged in four columns of four rows would be referred to as a 4 by 4 array. Using the four-by-four array, we can easily understand that they will have 16 oranges in total if each column represents a group of four oranges and if there are four rows of these groups. You can easily calculate this number by multiplying the number of items in each group by the total number of groups in the array rather than counting each orange individually or adding 4 + 4 + 4 + 4.
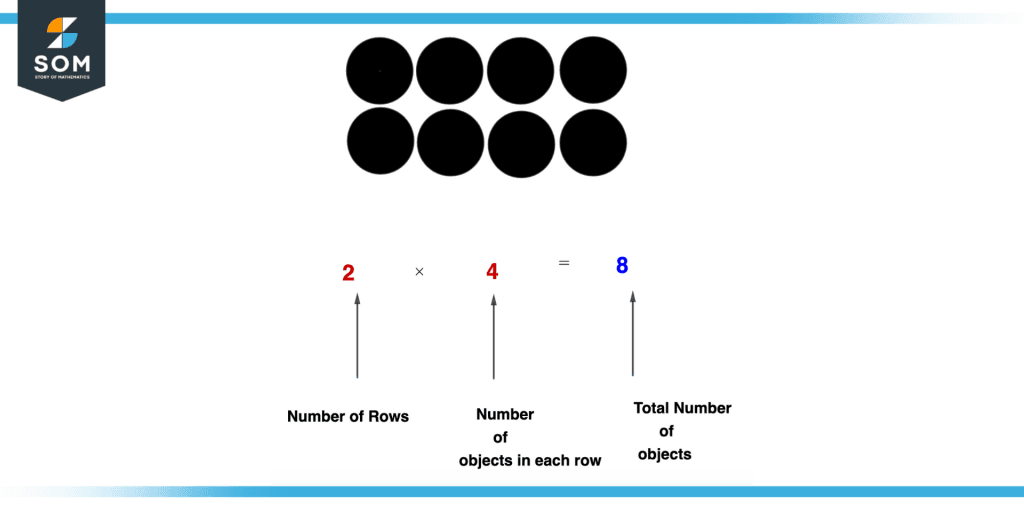
Figure 6 – Multiplication Using Array
Consider the above figure the concept of multiplication can be easily understood by the array as they act as a visual aid which makes it easier to understand. There are two rows and there are four objects in each row so we will simply multiply 2 by 4 which gives 8.
Demonstrating Division using Array
Suppose there are 16 oranges, and we are asked to divide these oranges among two people what we do will simply make an array of 2 by 8 as shown in the figure below.
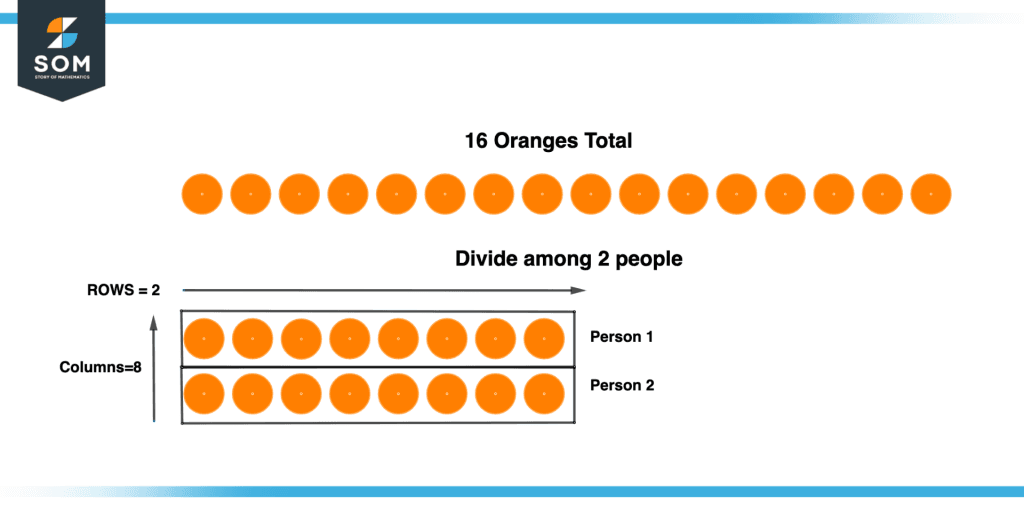
Figure 7 – Division Using Arrays
Demonstrating Inverse using Array
Suppose there are 9 circles, and they are represented as a 3 by 9 array we know that 3 multiplied by 3 equal 9 and we also know its inverse that 9 divided by 3 equals 3. In simple words division is undoing multiplication and multiplication is undoing division so there is an inverse relation between them that could be easily understood by the figure shown below.
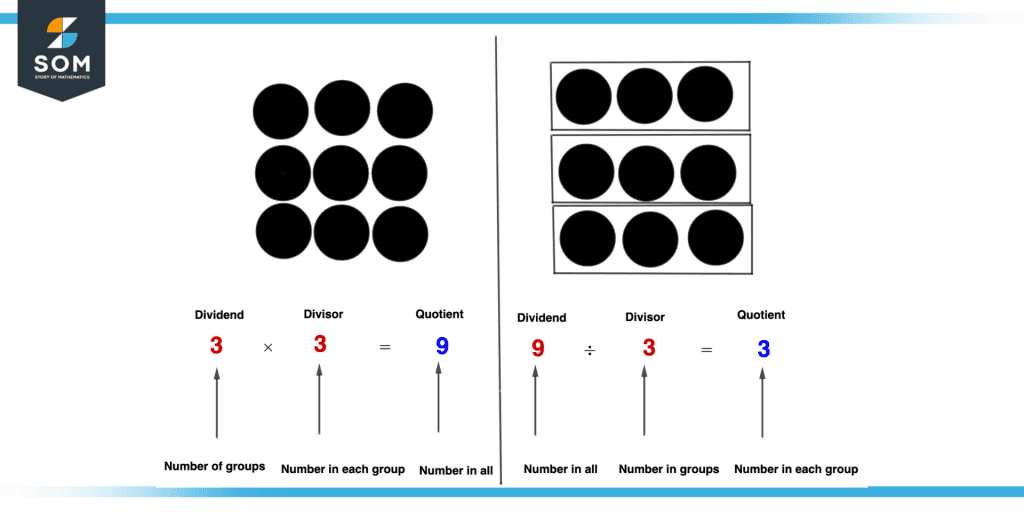
Figure 8 – Inverse of Multiplication and Addition
Commutative Property of Multiplication
Suppose we have 12 triangles, and they are represented in two forms of arrays.
The first form is that there are 4 rows and there are 3 objects in each row so multiplying gives a total of 12 triangles count.
The second form is that there are 3 rows and there are 4 objects in each row so multiplying gives 12 triangles count.
Thus, this proved the commutative property of multiplication whether the order or row or columns are interchanged the final product remains the same. The demonstration is shown in the figure below.
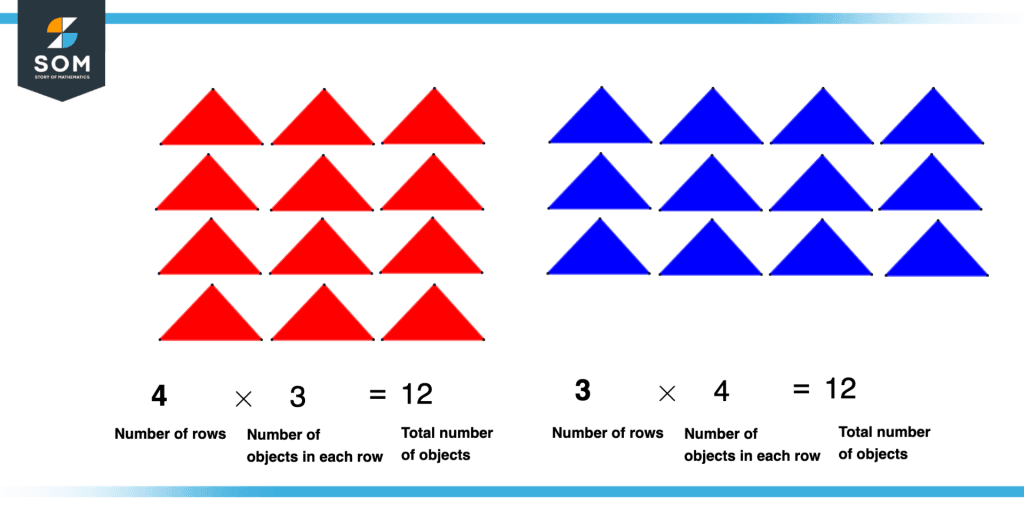
Figure 9 – Commutative Property of Multiplication using Arrays
Developing a fundamental understanding of these arrays as a whole will help us understand the interplay between multiplication and division, enabling us to perform more complex calculations as we advance into algebra and then advance mathematics.
Visual Examples
Consider the following figures, using the concept of array studied above write the number of rows, columns, and the total number of objects along with the array size/order for each figure.
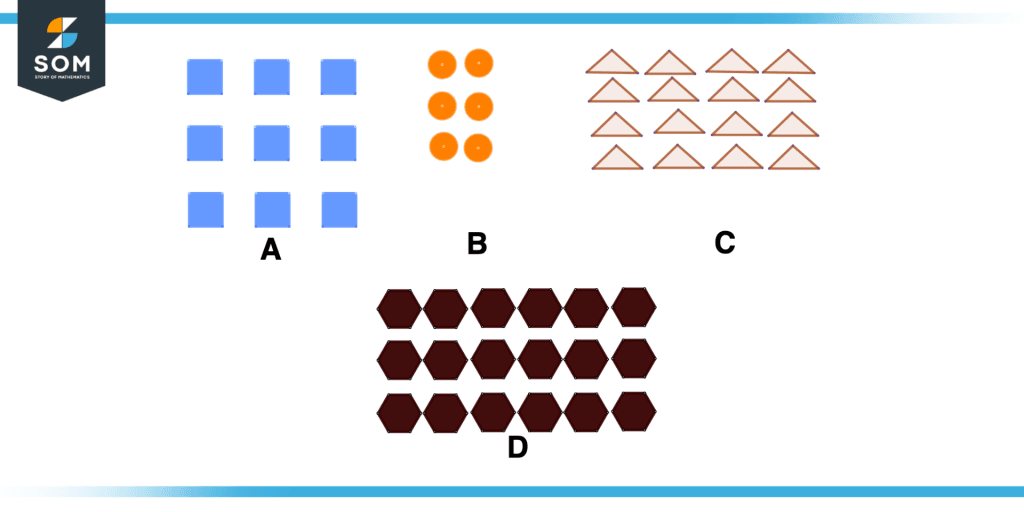
Figure 10 – Array Worksheet
Solution
In Figure A
Number of rows = 3
Number of columns = 3
Total number of objects = 9
Array size/order = 3×3
In Figure B
Number of rows = 3
Number of columns = 2
Total number of objects = 6
Array size/order = 3×2
In Figure C
Number of rows = 4
Number of columns = 4
Total number of objects = 16
Array size/order = 4×4
In Figure D
Number of rows = 3
Number of columns = 6
Total number of objects = 18
Array size/order = 3×6
Arrays are most useful when teaching students how to multiply and divide large shares of real objects, such as apples or oranges, since they help them understand how multiplication and division work practically. Students can use these visual representations to practice counting larger quantities of these items or dividing evenly among their peers by observing patterns of quick addition.
All mathematical drawings and images were created with GeoGebra.
