Ascending Order|Definition & Meaning

Ordering is of two types ascending order and descending order. Ascending order is basically an arrangement of numbers in series that starts with the lowest number and then ends at the largest number. Ordering and comparing are interconnected with one another. 

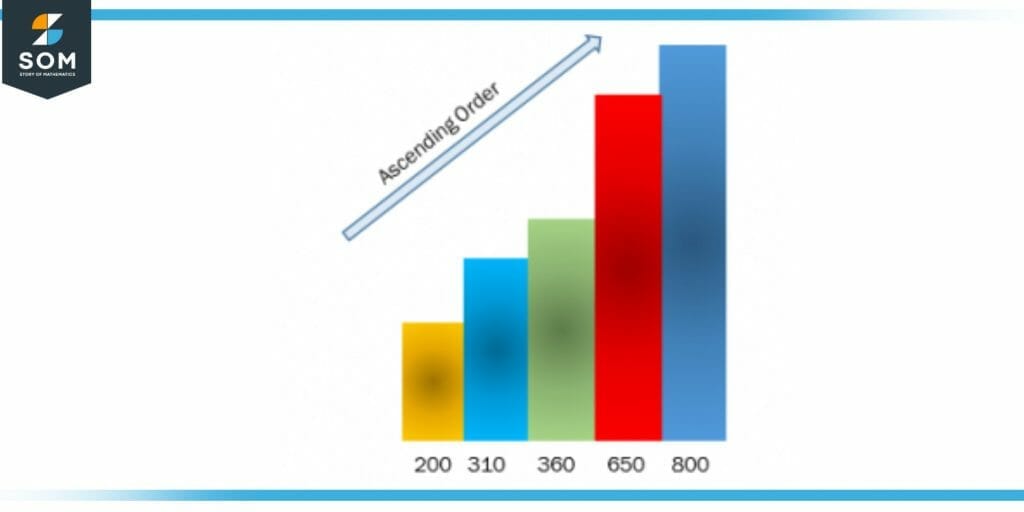
Figure 1 – Arrangement of numbers in ascending order

To order the number we must compare them first. The smallest number comes first and then at the end there will be the largest number from all.

Symbol of Ascending Order

We have two options for showing given values in ascending order: commas “,” or the “less than” symbol (<).” A less-than symbol, which indicates that the number on the left is less valuable than the number on the right side of that symbol, is the most typical way to show numbers in ascending order.

Arrangement of Numbers in Ascending Order

There is always a rule for solving problems, in ordering numbers there are also some rules which we need to cater to. Listed below are the rules for ascending order.

1. Determine how many digits each number has. The lowest number is the one with the fewest digits. First, draught it. Keep doing this until every number that is left for comparison has the same number of digits.
2. Start by comparing the numbers starting with the leftmost digit when two numbers have the same amount of digits. Put the smallest digit of the number in writing first.
3. Move to the numerals towards the right and then compare them if the digits on the left are the same. Make the first digit of the integer smaller.
4. Once we’ve arranged all the numbers, repeat the process with the remaining numbers.

Arrangement of Fractions in Ascending Order

Like numbers, fractions can also be arranged in ascending and descending orders. But the rule for ordering the fraction is a bit different for ordering numbers. The arrangement of fractions depends upon the denominator and numerator. Here is a detailed explanation of ordering fractions in ascending order.

Ordering With the Same Denominators

In the fraction the denominator is considered first, if the denominator is the same then the numerator will be compared. The smallest number on the numerator will come first in the order and so on in the end the greatest number in the numerator will be considered and come at the end.

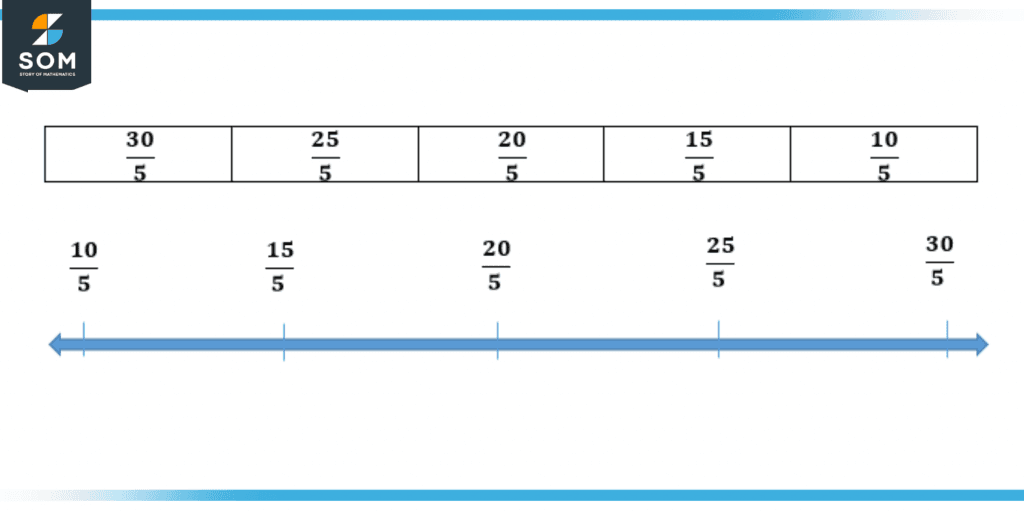
Figure 2 – Ordering same denominator Fractions in ascending order

Ordering With the Same Numerators

In the above section, we have seen the arrangement of fractions that have the same denominator, here we are considering an example of a fraction for which the numerator is the same. When the numerator is the same then the denominator with the highest numbers will be considered the smallest. Here in this example, there are 5 fractions 3/8, 3/7,3/5, 3/2, and 3/9. All the numerators are the same but the denominators are different the fraction with the highest denominators will be considered as smallest for here 3/9 will be the smallest and 3/2 will be considered as greatest.

Figure 3 – Ordering a fraction with the same numerator in ascending order

Ordering With Different Numerators and Denominators

Comparing can also be done when the numerator and denominator are different. The method for comparing these types of fractions is that first make the denominator the same and then compare the numerator. Here in the example below all the denominators can be made the same by multiplying and dividing with the same number like 2/5 x 6/6, 4/6 x 5/5, 3/5 x 6/6, 1//3 x 10/10, 5/2 x 15/15. Here at the end, the denominator for all the fractions will be the same that is 30. After making the denominator the same compare the numerator, the smaller the numerator least the fraction will be, bigger the numerator greater the fraction will be in the order.

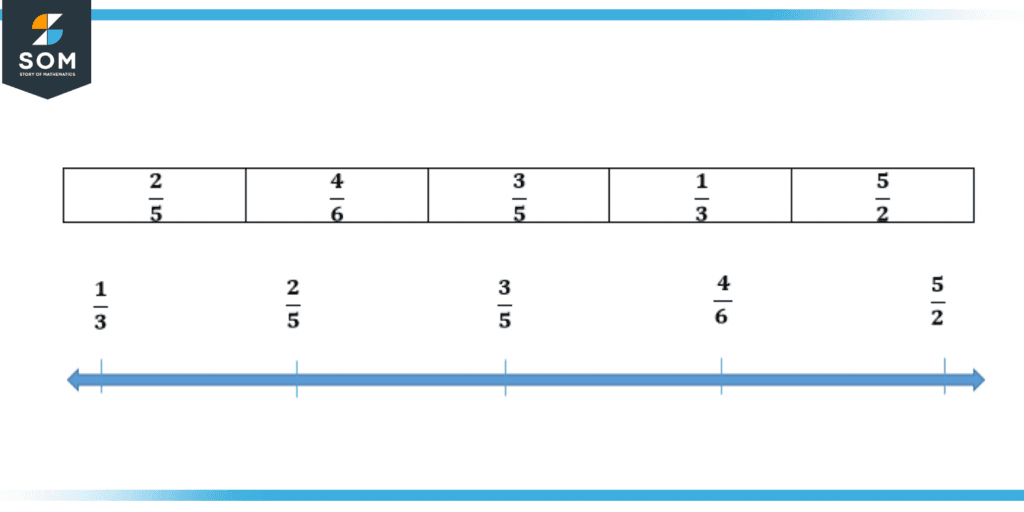
Figure 4 – Ordering a fraction with different numerators and denominators in ascending order

Ascending Order Applications in the Real World

The arrangement is basically sorting things or numbers in order which is then easy to assess for later times. We often apply to sort in our daily life in many ways. The English alphabet letters are arranged in ascending order from A to Z. The weight and height of people can be arranged in ascending order. The top advantage of sorting is that it makes our searching easy and quick. Sorting is of fundamental use in a computer database as well.

The arrangement is of great importance in scientific concepts so the things can be arranged in the corresponding order effectively and efficiently.

Ordering Examples

Example 1

Arrange the following numbers in ascending order: 22.44, 22.60, 22.45, 22.04, 22.40.

Solution

First of all, in the case of decimal numbers compare the parts of the whole number. The smallest whole numbers will be in the lowest order and the bigger whole number will be the largest in the order.

If the whole number is the same then we will compare the decimal part same as we compared before the whole number part.

Figure 5 – Ordering decimal numbers in ascending order

Example 2

Arrange the following numbers in ascending order: -56, -1, -4, -56, -34.

Solution

Negative numbers should be arranged in an ascending sequence from the smallest to the largest values. It is crucial to understand this because negative numbers are confusing because the absolute values of smaller numbers are generally higher than those of bigger ones.

The largest negative number has the lowest value when using negative numbers. Therefore, if you need to arrange as -34, -56, -63, -1, and -4 in ascending order, do it as follows:

-63 < -56 < -34 < -4 <-1

Out of the four numbers presented, -1 is the biggest, and -63 is the smallest.

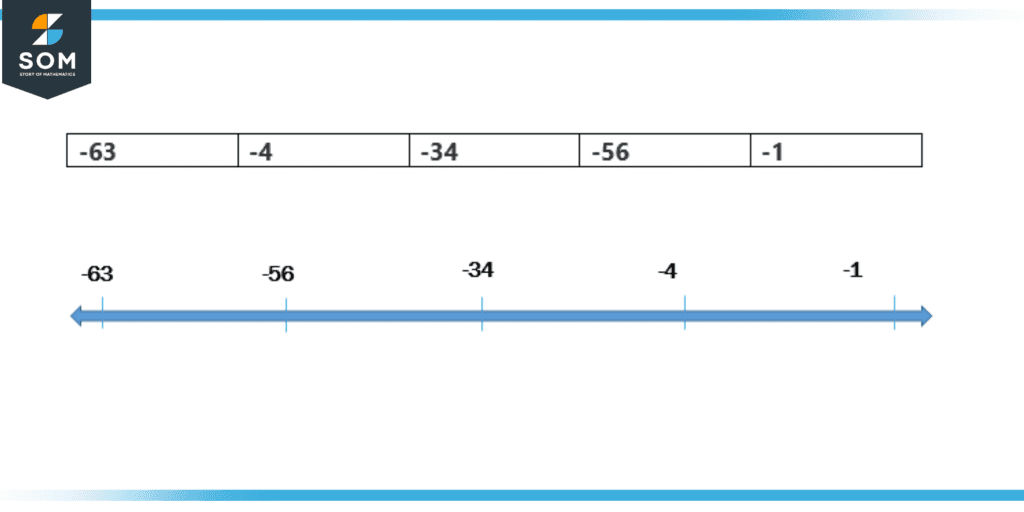
Figure 6 – Arranging negative numbers in ascending order

The above figure gives a complete description of the arrangement of negative numbers. In a negative number, the greater number with the negative sign will be the smallest and the smaller number with the negative sign will be the greatest.