JUMP TO TOPIC
Associative Law|Definition & Meaning
Definition
Associative Law states that if three or more real numbers are added or multiplied, their association or grouping or order does not matter, it always gives the same result.” In a group of three digits that are being added or multiplied, it makes no difference in the consequences if the order of the group or subgroups is changed.
Introduction to the Associative Law
In Mathematics, this law is applicable to the addition and multiplication of three or more numbers. This law is expressed as follows for the three numbers being added or multiplied.
(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c)
The above expressions clarify that the association or grouping of numbers for addition and multiplication is independent and does not affect the results. It does not matter how we group or order them in a group.
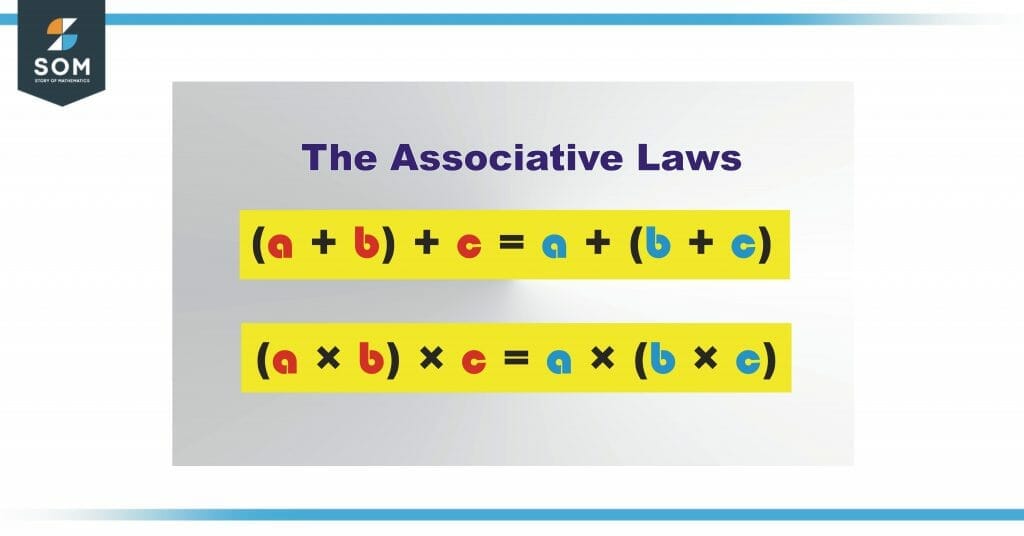
Figure 1 This image shows the two types of associative laws i.e Additive Law and Multiplicative Law
If we apply this law to other arithmetic operators like subtraction and division, it fails. This is because there is a change in the results if this law is applied for subtraction or division.
So out of four basic operators, i.e., addition, subtraction, multiplication, and division, associative law only holds for addition and multiplication. This law is also known as the Associative Property of multiplication and addition.
The associative law also holds for vectors that are usually used in physics. It says that the sum of vectors remains constant even if the order of vectors is changed.
Formulae for Associative Law
As per the definition of Associative law or property, the formulae can be generated easily and simply. According to the basic definition, the first thing that we know is it is only applicable for pure addition or multiplication expression.
If the first condition is confirmed then the next thing is that associative law exists for at least three or more terms or numbers in an expression.
And the final thing is that if there are three numbers and they are being added or multiplied, the grouping of these numbers for addition or multiplication does not matter which means we can group in any order.
So, keeping the above points in mind, the formulae for the Associative law can be written for three numbers A, B, and C:
A + (B + C) = (A + B) + C
A × (B × C) = (A × B) × C
Classification of Associative Law
Based on the arithmetic operation, associative law is classified into two types i.e Associative Law of Addition and Associative Law of Subtraction. Following is a brief description of these types
Associative Law of Addition
The Associative Law of addition states that the process or the operation of addition obeys associative law which means that the change in order or grouping of numbers in an expression of numbers does not affect the final results. Its mathematical representation is given below.
A + (B + C) = (A + B) + C
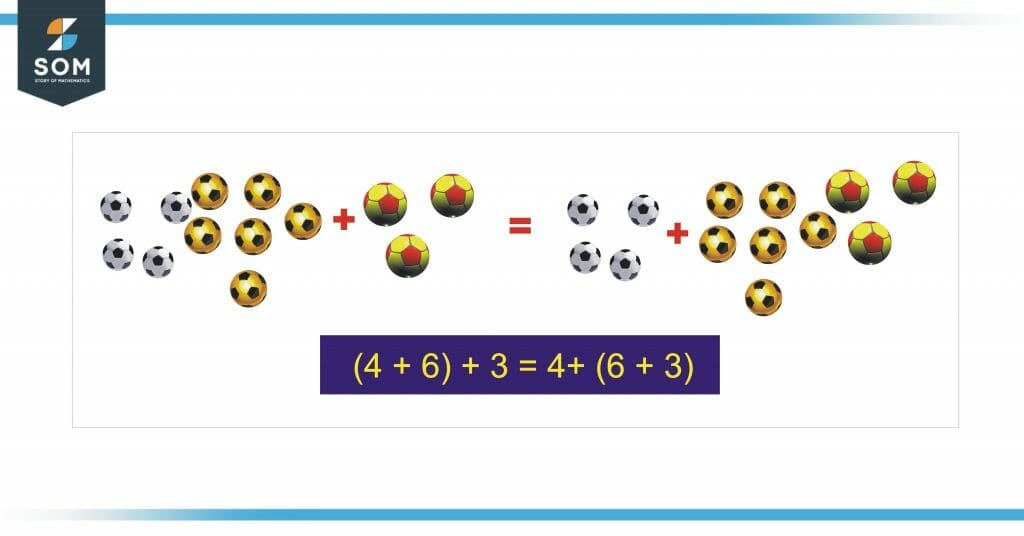
Figure 2 Image shows the addition of three different types of footballs. We can first add two types and then add the third one or we can add the second and third and then add the sum to the first type, the result remains the same. This is an example of additive property
Associative Law of Multiplication
The Associative Law of multiplication states that the process or the operation of multiplication obeys the associative law which means that the change in order or grouping of numbers in an expression of numbers does not affect the final results. Its mathematical representation is given below.
A × (B × C) = (A × B) × C
Why Does the Associative Law Not Apply to Subtraction and Division?
A common question that arises when we study Associative law is why this law is not applicable to all four basic arithmetic operators i.e. Addition, subtraction, multiplication, and division. It holds only for addition and multiplication and not for the other two.
The reason is based on the purely mathematical and simple logic that when the associative law is applied to subtraction or division it gives different results for different groups of the same numbers.
Let us understand this concept with one example for each case
We are given three numbers as
20-5-1
According to the associative law:
(20-5)-1 = 20 – (5 – 1)
Solving the L.H.S of the equation:
(20 – 5) – 1 = 15 – 1 = 14
Now, R.H.S:
20 – (5 – 1) = 20 – 4 = 16
As we can clearly see that L.H.S is not equal to the R.H.S, hence it is proved that associative law does not hold for subtraction.
Now we will apply associative law for division and check its validity.
We are given 36 ÷ 6 ÷ 3
Applying associative law:
(36 ÷ 6) ÷ 3 = 36 ÷ (6 ÷ 3)
Solving L.H.S:
(36 ÷ 6) ÷ 3 = 6 ÷ 3 = 2
Now solving R.H.S:
36 ÷ (6 ÷ 3) = 36 ÷ 2 = 13
Hence, it is clear that R.H.S is not equal to the L.H.S. So, associative law does not hold for the division also.
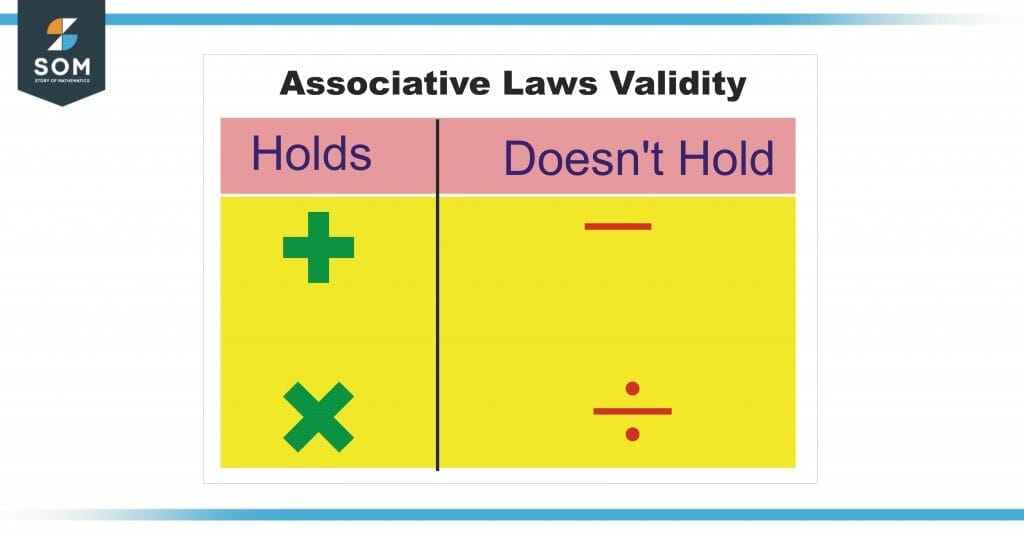
Figure 3 This table represents the validity of associative law for basic arithmetic operators.
Some Examples of the Associative Law in Action
Example 1
Solve the following expressions to verify the Associative Laws of addition and multiplication.
- (1 + 2) + 3 = 1 + (2 + 3)
- (1 x 2) x 3 = 1 x (2 x 3)
Solution
First, we solve:
(1 + 2) + 3 = 1 + (2 + 3)
Solving L.H.S:
(1 + 2) + 3 = 3 + 3 = 6
Now, solving R.H.S:
1 + (2 + 3) = 1+ 5 = 6
As L.H.S is equal to the R.H.S, we have verified that the associative law holds for the Addition operation. Now, we move on to the next part of the question:
(1 x 2) x 3 = 1 x (2 x 3)
Solving L.H.S:
(1 x 2) x 3 = 2 x 3 = 6
Similarly solving R.H.S:
1 x (2 x 3) = 1 x 6 = 6.
As L.H.S = R.H.S, hence proved that associative law also holds for multiplication.
Example 2
Jon is a grade 1 student and he knows that 3 × 2 = 6. His teacher asks him to solve and find the value of 3 × 2 × 4. Help Jon in finding the correct answer using your ability to use the Associative Law of Multiplication.
Solution
As we know,
the Associative property of multiplication states that
3 × 2 × 4 = (3 × 2) × 4
Jon already knows that 3 × 2 = 6.
So,
We can write as
(3 × 2) × 4 = 6 × 4 = 24.
Therefore the correct answer is 24.
All images/mathematical drawings were created with GeoGebra.
