JUMP TO TOPIC
Arithmetic Sequence|Definition & Meaning
Definition
A list of numbers where subtracting two consecutive entries results in a constant difference is an arithmetic sequence. This difference is called the common difference of the sequence.
In that sense, the set of odd integers is an arithmetic sequence with a common difference of 2
since 3 minus 1, 5 minus 3, and any other consecutive pair’s difference is equal to 2.
What Is an Arithmetic Sequence?
The arithmetic sequence is a sequence in which the expected difference between any two successive terms remains the same. Let us go back and review what a sequence is. A set of numbers arranged in a specific order is called a sequence.
For instance, the sequence 1, 7, 12, and 17 is an example of an arithmetic sequence since there is a sequence where each number is created by adding 6 to the phrase that came before it.
The following steps form an arithmetic sequence since each term is obtained by adding a constant number four to the phrase that came before it.
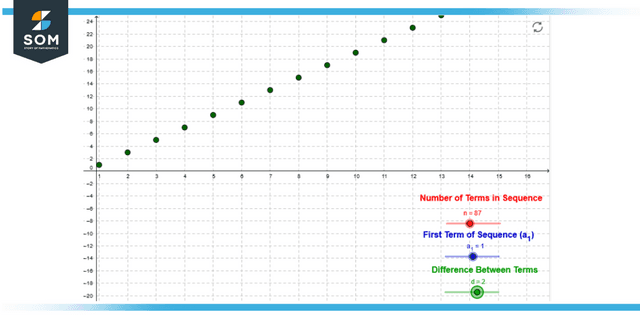
Figure 1: Graphical representation of the arithmetic sequence.
There are two different formulas for arithmetic sequences.
- A mathematical expression that locates the nth element of a sequence.
- A mathematical expression that finds the sum of an arithmetic sequence’s first n terms.
We can use the formula for the arithmetic sequence to locate any term in the arithmetic sequence if that is what we need to do. To achieve a deeper comprehension of the topic, let us first examine the definition of the arithmetic sequence and then proceed to study the formulae, which derivations and several further examples will accompany.
There are two ways to define what is known as an arithmetic sequence. “sequence where the difference between every two succeeding terms is identical” is one definition of it. In contrast, “in an arithmetic sequence, “every term is formed by adding a specific number (positive or negative or zero) to its preceding” another.
Example of Arithmetic Sequence
Consider the sequence: 4, 7, 10, 13, 16. This is an arithmetic sequence since each phrase in the sequence can be created by adding a constant number (3) to the value of the preceding item in the sequence.
The initial number, notated as ‘a’, is 4, so a = 4. The common difference, d, is calculated as follows:
(7 – 4) = (10 – 7) = (13 – 10) = (16 – 13) = … = 3
As a result, the notation for an arithmetic sequence looks like this: a, a plus d, a plus 2d, a plus 3d, and so on.
Calculating the Nth Term of an Arithmetic Sequence
The formula for determining the nth element of an arithmetic series, such as a1, a2, a3, …, is a = a1 + (n – 1) d. The arithmetic sequence can also be referred to by its broad name, the general term. This is a logical conclusion that may be drawn directly from the realization that the arithmetic series a1, a2, a3, … = a1, a1 + d, a1 + 2d, a1 + 3d, …
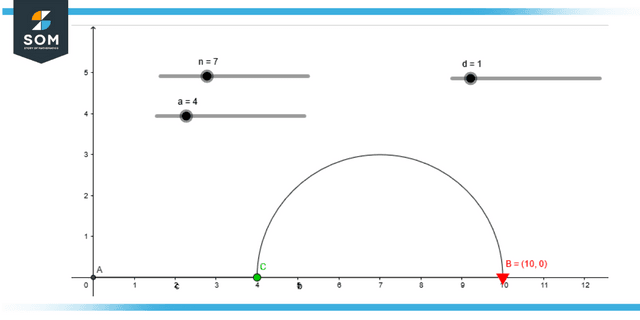
Figure 2: Illustration of nth term of arithmetic sequence.
The Formula for the Arithmetic Sequence
The letter a denotes the beginning of an arithmetic sequence, and the letter d denotes the sequence’s common difference. The number n denotes the total number of terms. The AP can be written in any generic form: a + d, a + 2d, a + 3d, etc., up to n words.
A specific arithmetic sequence can be used to compute the nth term, the summation of n terms of an AP, or the common difference of a given arithmetic sequence using one of several possible formulae related to the series.
The Recursive Formula for the Arithmetic Sequence
When the value of ‘a1‘ and ‘d’ are known, the formula just presented for determining the nth term of an arithmetic series can be used to determine any term of the sequence. The “recursive formula of an arithmetic series” is another formula that may be used to discover the nth term.
This formula is applied to find a term (an) of the sequence when its preceding term (an – 1) and ‘d’ are known. It says a = an – 1 + d
This formula adheres to the requirements outlined in the concept of the arithmetic sequence.
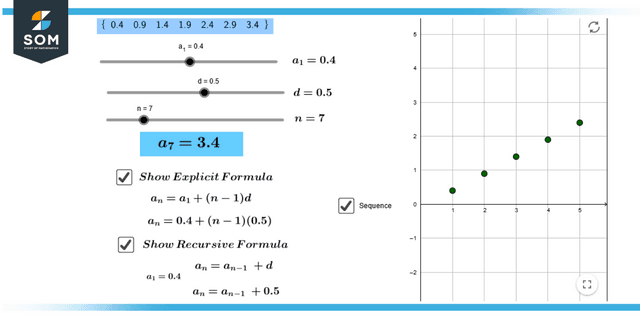
Figure 3: Representation of recursive formula of arithmetic sequence.
Properties of Arithmetic Sequence
The common difference, represented by the letter dd, is the difference maintained between all and all pairs of numbers that are consecutive or subsequent in a sequence. We will employ the common difference to get from one phrase to another. How?
The following term can be arrived at by taking the present term and adding the common difference to it, and so on. The terms in the sequence are created in such a way as to do this.
- If the average difference between two consecutive terms is positive, then we state that the sequence is rising.
- Conversely, we conclude that the sequence declines when the difference between the two values is negative.
- The difference in value between any two numbers that are sequential in an arithmetic sequence is always the same.
- An arithmetic series, a1, a2, a3,… have a common difference that can be expressed as the formula d = a2 – a1 = a3 – a2 = …
- An arithmetic series has the following formula for its nth term: a = a1 + (n – 1)d.
- Arithmetic sequence
- s’ differences can be positive, negative, or zero. All three outcomes are possible.
Examples of Arithmetic Sequence Operations
Example 1
In the following arithmetic sequence, figure out the next three terms:
9, 18, 27, 36.
Solution
First, determine the common differences:
18 – 9 = 9
27 – 18 = 9
36 – 27 = 9
So d = 9
Now add the common difference to the last term, then to the result, then as often as required.
36 + 9 = 45
45 + 9 = 54
54 + 9 = 63
Example 2
Find the 28th term of the given sequence
2, 7, 12, 17, 22, 27, 32, …
Solution
a = 2
d = 5
a28 = 2 + (28 – 1)5
2 + (27)5
2 + 135 = 137
All images/graphs are created using GeoGebra.
