Area|Definition & Meaning

Introduction to Area 

The area is the space used up by any object in a 2D plane. We can find the area of all types of shapes by finding the product of the length and the width of the object. If we consider a rectangle that is made up of small unit squares so the area we will be considered as only those unit squares which are required to fill up the exact position of the rectangle.

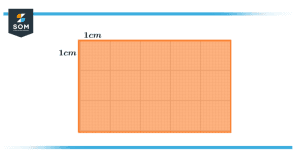
Figure 1 – A rectangle divided into square units of 1cm

Difference Between Area and Perimeter

Area and Perimeter seem quite similar and often are confusing, but actually, these two are very different from each other. As we know, the area is the amount of space occupied by any object in a 2D plane. Each shape depends on its dimensions when we are talking about the area.

The perimeter is the boundary that encloses any shape or any object. It depends on the length of its shape rather than the dimension.

Note that any 2 shapes with the same area can have different perimeters and any 2 same perimeters can have shapes with different areas

For example, if you have a garden that needs to be fenced, so the flight of the fencing material or the boundary itself will be known as the perimeter whereas the garden itself will be the area that fills the space within the boundary.

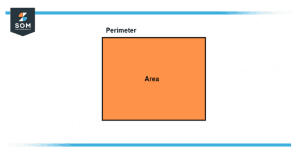
Figure 2 – A square representing both Area and Perimeter

Detailed Overview

To grasp the concepts we are going to find the area of a square as it is quite easy to understand. As we know that each side of a square is equal so when we will multiply them together, we will get our area. Let us take this example:

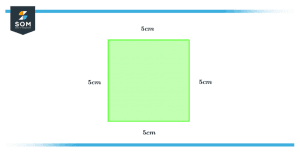
Figure 3 – A square with 5cm sides

In this example, we will first identify the length and width. As it is a square so all sides will be equal hence both its length and width are 5cm. Now to find the area of this square we will put the values in the following formula:

Area = l * w

Area = 5cm * 5cm

So the Area of this square is 25 squared cm.

We can also find the area of any object by using the grid as we know that area of an object can be defined as the number of unit squares that can be fit in. so let us take this figure as an example:

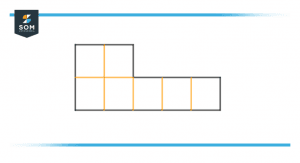
Figure 4 – A Shape divided into square units or grid

In this figure, we can see an object with a grid defining all the square units present in the object. To find the area of this figure we will count all of the square units.

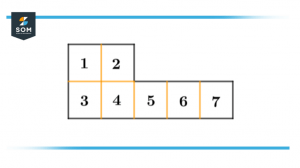
Figure 5 – Numbered Grid representing the Area of the shape

We will check for any half square in the figure if they are not present then we will count the remaining squares. From this figure, we can find the area of the object which is 7cm.

Pictorial Representation

We can find the area of different objects depending on their shapes. For each shape, we have a different set of formulas. For example, if we take a square:

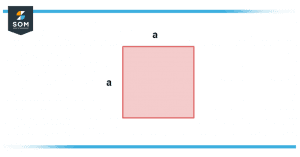
Figure 6 – Area of a Square

As we already know that in a square all sides are equal so no matter which 2 sides you choose the product will always be the same. Hence the area of a square can be written as:

Area = a$^2$

We can also use the grid method to calculate the area by counting all of the unit squares present in this region

Now let us take an example of a rectangle:

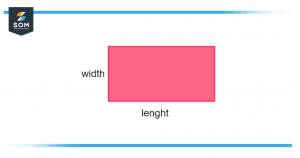
Figure 7 – Area of a Rectangle

To find the area of a rectangle we will find its length and width and multiply them to get our result. As we know that length is unidimensional so normally it is measured in feet, inches, yards, etc. but since the area of any object is 2D so we calculate it in square units.

From the figure, we can see that length and width are required for a rectangle, so the area can be written as;

Area = L * W

Now, if we take a circle:

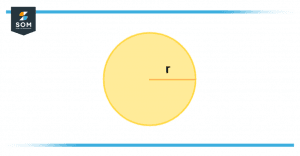
Figure 8 – Area of a Circle

A circle does not have a corner rather all its sides are curved. The area of a circle will be all of the space taken up within the boundaries of the circle itself. Now to calculate the area of a given circle, we will first find the total distance of the line formed from the center point of the circle to the circumference of that circle.

For this, you need to be aware of the concept of the radius of the circle which is the total length of a line segment formed from the center of the circle to the circumference of the circle. So we will use this formula: 

Area = $\pi$r$^2$

Here π is equal to 3.14 and r is equal to the radius of the circle.

By using these concepts we can find the area of a triangle.

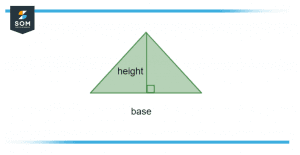
Figure 9 – Area of a given Triangle

To find the total area of any triangle we should always keep the height and base in mind, for that we will use this formula:

Area = $\mathsf{\dfrac{1}{2}}$ x b x h

Finding Area of Complex Shape

If you have to find the area of complex shapes or composite figures, then you can simply divide the shape into smaller regular parts so that you can find the area of individual parts and can add them later on to calculate the area of the given figure.

For example, you have been given the following shape:

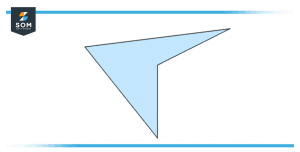
Figure 10 – An irregular shape

First of all, we are going to partition this figure into small regular parts

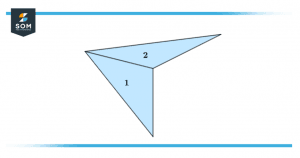
Figure 11 – Irregular shape has been partitioned into 2 parts

Now as we have two triangles due to the partition and due to our understanding we are now aware of how to calculate the area of the triangle we will use that formula. Once we have the area of both triangles then we will add these areas to get the total area.

Solved Examples of Area

Example 1

Emma is in an architecture firm. She has been allotted a task to find the area of a rectangle for the swimming pool. The length of the rectangle is 12m and the width is 6m. Find the area.

Solution

To find the area of any rectangle, we use this formula:

Area = L * W

As we have been given both the length and width so we will put them in the equation:

Area = 12 * 6

Area = 72

So the total area of the swimming pool is 72 squared m.

Example 2

Find the area of a rectangle with these dimensions

Length: 15cm

Width: 7cm

Also, find the area when the width is 4cm.

Solution

As we know that the area of a rectangle is given by the product of its width and length so we will calculate the area of the given rectangle by using this formula:

Area = L * W

Now putting values:

Area = 15 * 7

Area = 105

So the Area of this rectangle is 105 squared cm.

Now changing the width we get:

Area = 15 * 4

Area = 60

Now the area of the rectangle is 60 squared cm.

Images/mathematical drawings are created with GeoGebra.

Arc Definition < Glossary Index > Arithmetic Sequence Definition