Arc|Definition & Meaning

The concept of arc is a is a very fundamental idea commonly used in geometry. An arc is any curved surface or path. Arcs may be associated with all geometrical shapes containing some curved or arched boundary. 

Commonly used arcs may belong to circles and parabolas. Both of these examples hail from a class of second degree polynomials. However, the general idea or arc is not limited or restricted to any particular standard geometrical shape. Its just a curved path (any curved path).

Explanation of Arc With Visual Intuition

The core idea of an arc can be understood with the help of examples. Following figure shows a circle and highlights an example of arc.

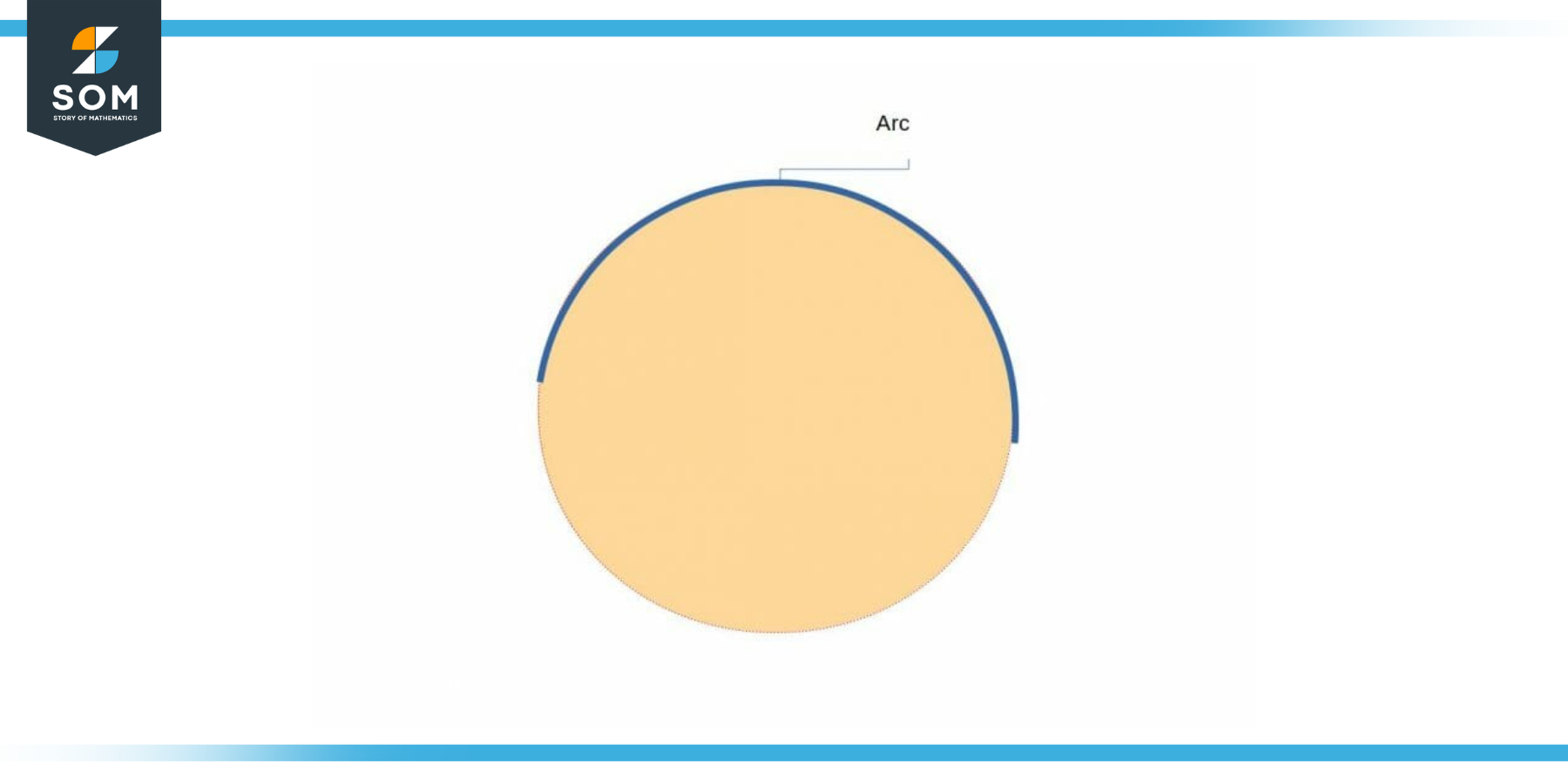
Figure 1: Arc of a Circle

It can be seen that an arc of a circle is nothing but a piece or segment of its circumference which is shown in blue color. Following figure shows another example of an arc but here we use parabola for the demonstration.

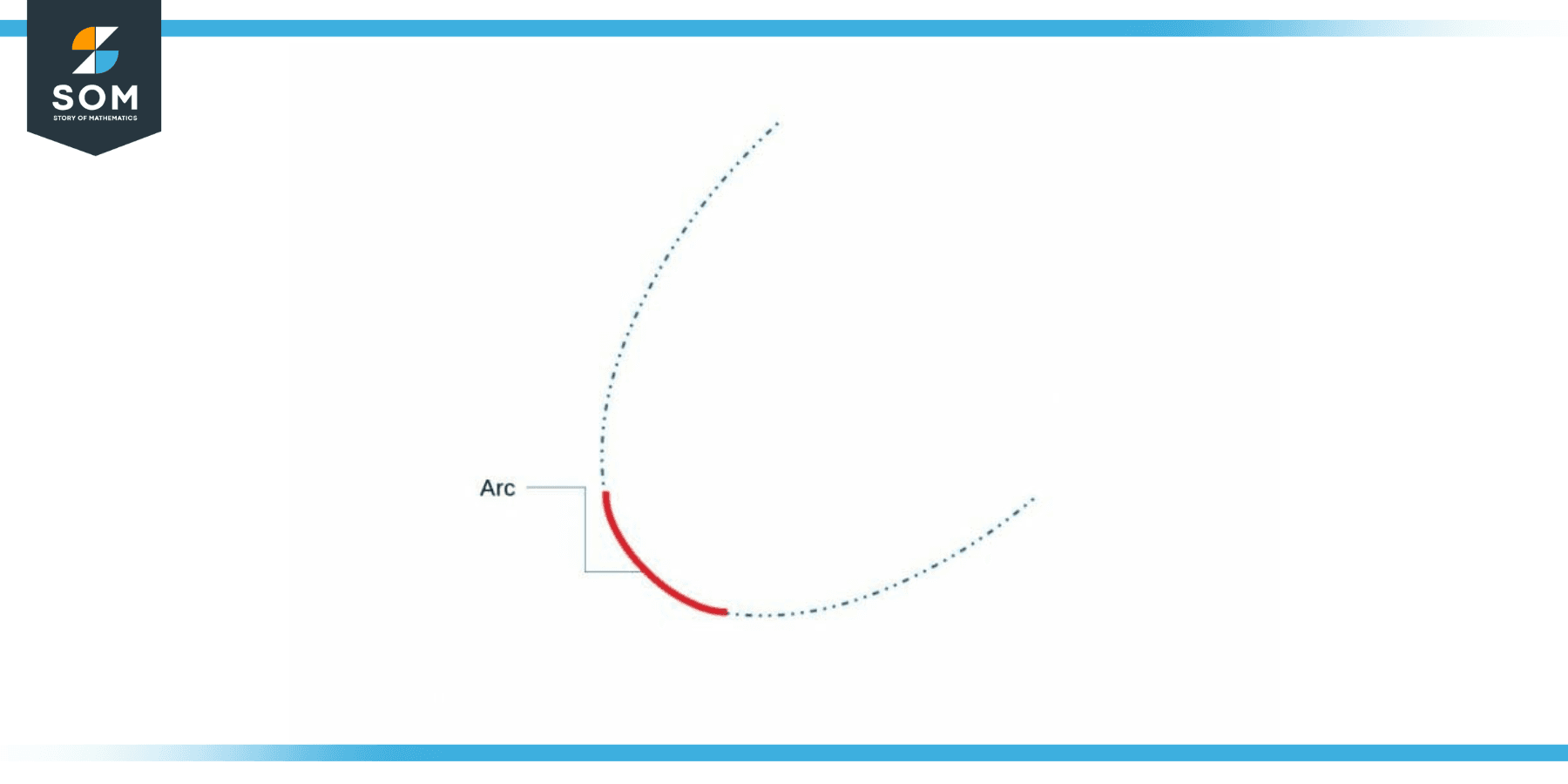
Figure 2: Arc of a Parabola

In the above figure the red solid line shows the arc whereas the blue dotted line represents the total path of the parabola. The concept of arc is not limited to the circles or parabolas. In fact in its general form, an arc can be along any curve. Following figure shows an arc along a higher degree polynomial.

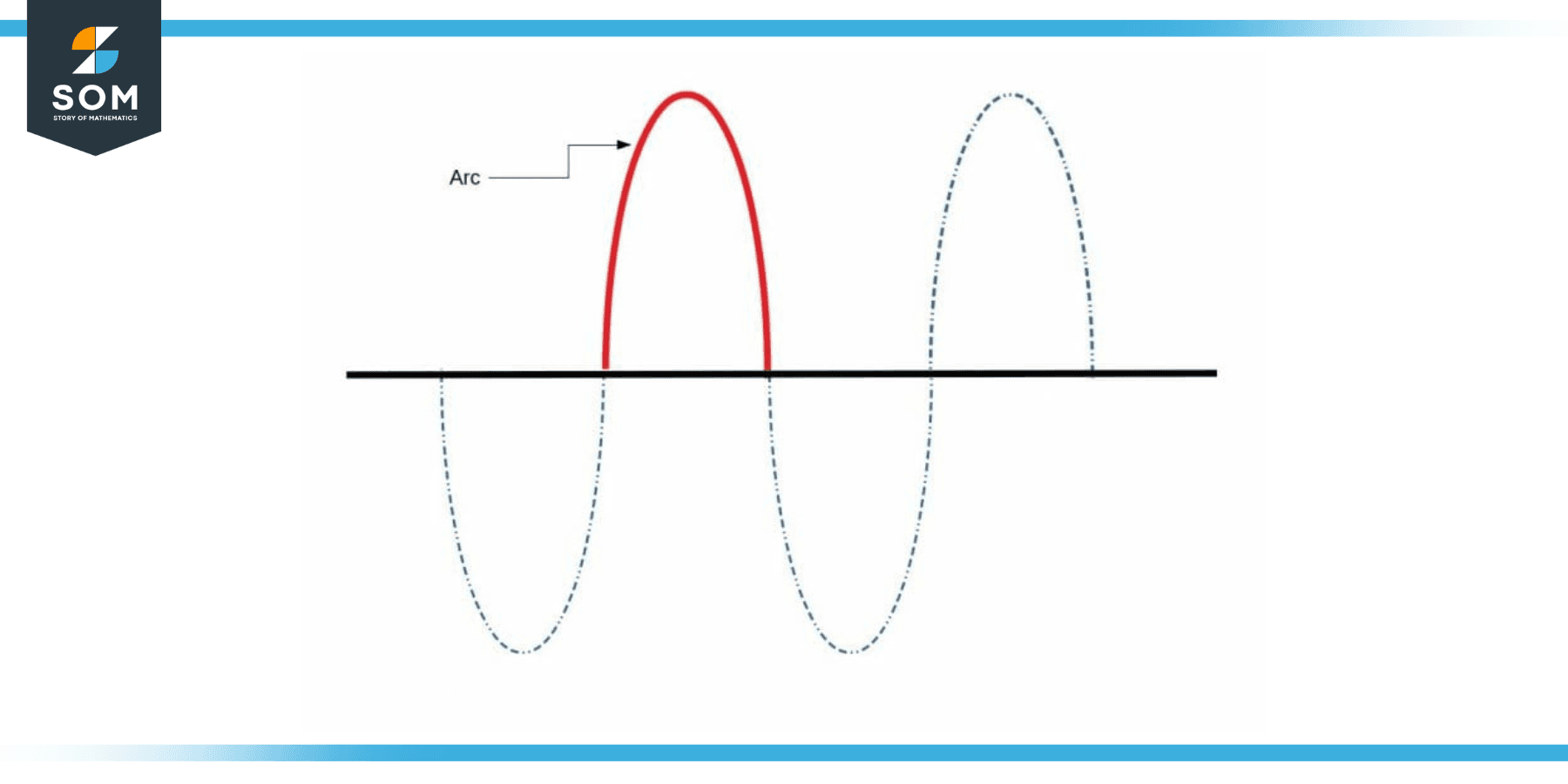
Figure 3: Arc of a Higher Order Polynomial

In the above figure the red solid line shows the arc whereas the blue dotted line represents the higher order polynomial. The striking similarity between above curve and the sinusoidal function is intentional. This is just to show that the same concept can be extended to any mathematical function that contains some curved path.

Now that we have understood the basic concept of an arc in reference to geometry, we can now delve into its different types. Lets consider the case of a circle. A circle may have three types of arcs. If the arc covers the less than half of the total circumference of the circle then its called a minor arc. If an arc covers more than fifty percent of total circumference of the circle, its called a major arc.

The borderline case where the arc traverses exactly 50 percent of half of the total circumference is commonly termed as a semi circle. A semicircle, understandably is just a half circle which is actually an arc.

In many geometry problems it may be necessary to find the length of an arc. Let us consider the simplest case of a circle as shown in the figure below:

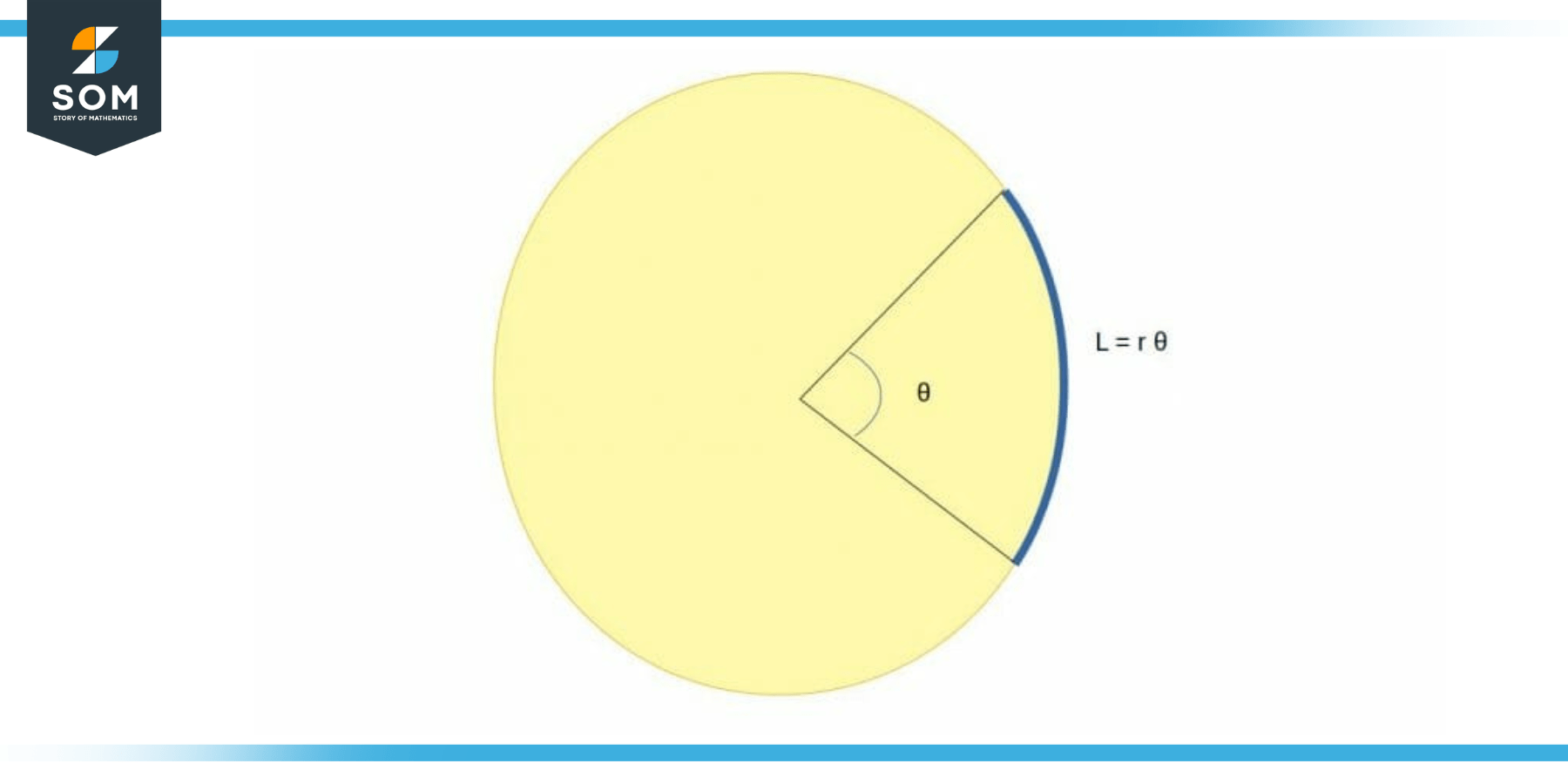
Figure 4: Arch Length of a Circular Arc

The segment shown in blue is an arc of length equal to L. This arc makes an angle of θ degrees at the center of the circle. Now to find the arc length, we can use the following formula:

L = r θ

Where, r is the radius of the circle.

Arcs are very common in daily life. A rainbow, a curved road, a bowl, the path of a rocket etc. are all examples of the arc. The formula presented above, can be used to solve many types of numerical problems. Suppose a rocket is fired at some angle with the horizon. The path along which the rocket is moving is of a parabolic shape.

Now if you wanted to calculate the distance traveled by the rocket, you would need to calculate the length of the arc or the curved path along which the rocket had moved. Similarly if you were traveling in a car along a curved road, you would use the same concept of the arc lengths to evaluate the distance.

For larger distances such as the ones used in astronomy, the concept of arc length may be used to find the size of an object. This method is used to find the size of Sun and the Moon. In this case one simply needs to measure the angle that the body generates at the eye of the observed and the distance of the object from the observer.

Once you have these two things, using the above formula, size L of the object can easily be calculated. The converse formula can also be used where the size of the object is known and we need to find the distance to that object. This calculation may be used to find the distance to objects on earth surface since we know the sizes of most of the objects on Earth.

Solving Numerical Problems Related to Arc Length

Lets now introduce the formal method of calculating an arc length.

– First step is to see what data is given. Normally two out of the three parameters ( L, r & θ ) are given.

– Secondly find the required quantity by using the formula L = r θ directly or after some manipulation ( i.e. L / θ = r or θ = L / r )

– It should be noted that the value of the angle used in this formula is in radians. So you may have to convert the angle from degrees to radians.

(a) Suppose a car is moving along a curved road. As it moves along this path, it covers a distance of 10 meters. If the circular angle covered by the car is 180 degrees, find the radius of the circular path.

(b) Suppose a rocket was launched from the ground and it followed a circular trajectory during its flight before hitting the ground. Given that the maximum height of the rocket was 1000 meters, find the length of its trajectory.

(c) A bicycle covered a distance of 0.5 meters. If the radius of its wheel is 1 meters how much did the wheel turn (in degrees).

Solution

(a) Given that:

L = 10 meters

and

θ = 180 degree = π radians

Using the formula:

r = L / θ = 10 / π = 3.18 meters

(b) Given that:

r = 1000 meters

and

θ = 180 degree = π radians

Using the formula:

L = r θ = 1000 x π = 3141.6 meters

(c) Given that:

L = 0.5 meters and r = 1 meter

Using the formula:

θ = L / r = 0.5 / 1 = 0.5 radians = 28.65 degrees

All mathematical drawings and images were created with GeoGebra.

Approximation Definition < Glossary Index > Area Definition