JUMP TO TOPIC
Approximation|Definition & Meaning
Definition
An approximation means that the result is closer to the actual value but not equal. An approximation can be made by either rounding off to the nearest 10 or 100 or rounding them to the nearest decimal place.
You can approximate a number if the value is very high or low. For example, the distance between the moon and the earth is 384,400 km, but we can write the approximate length, which can be 384,000 km. Approximation helps us simplify our mathematical solutions.
We use the $\approx$ symbol to represent the approximation between the numbers.
Visualizing Approximation
We can illustrate how approximation can be represented using the following figure 1.
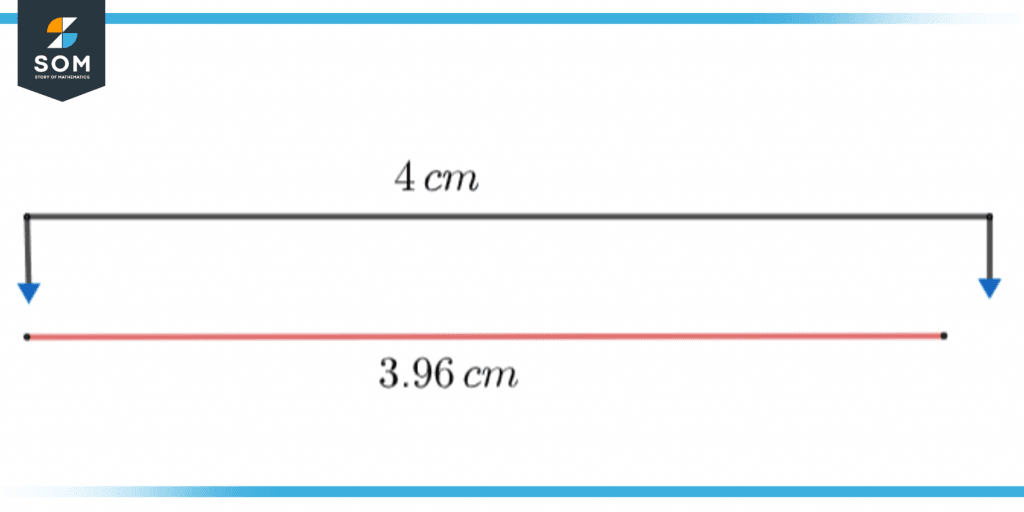
Figure 1 – Illustration of approximation.
Imagine the red line as a piece of pipe. The exact length of the tube is 3.96 cm. We can use approximation and say the pipe is approximately 4 cm long. This statement would be correct and provide us with the approximate value of the tube.
Looking at Figure 2 below, we can see that the radius of the smaller circle is 5.89 cm. We can use approximation and represent the same circle with a radius of 6cm. The value would be correct for the radius as well.
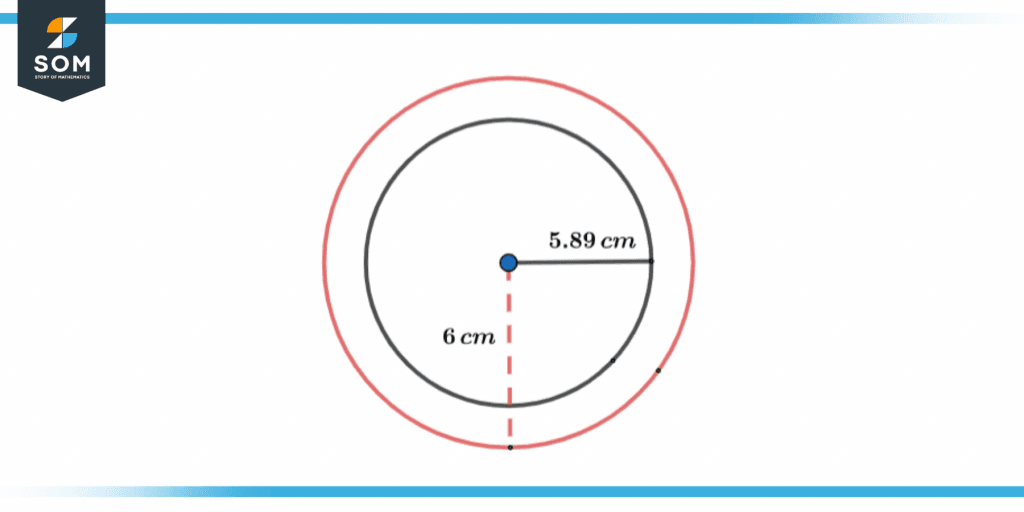
Figure 2 – Circle radius approximation.
Figure 3 below also illustrates how approximation is made. The figure shows two rectangles; one is blue, and the other is red. The blue rectangle has dimensions of 9.8m x 7.8m. The red rectangle approximates the blue rectangle with dimensions of 10m x 8m. Both rectangles are similar in dimensions.
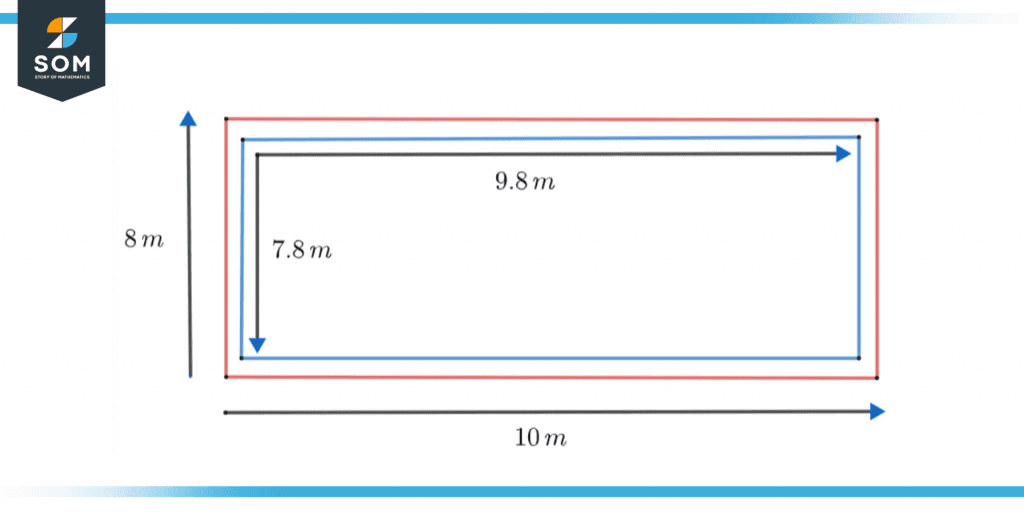
Figure 3 – Approximation of rectangle.
Rounding Numbers for Approximation
Rounding numbers refer to changing a number’s digits to approximate a value. This value more simply represents the given number. For instance, 400,000 rather than 397,894 could describe a town’s population.
Calculations are made easier by rounding numbers, producing a simple number to recall. The only numbers for which rounding is done are those for which the exact value is not all that significant.
Numbers may be rounded to various digits, such as the nearest ten, hundred, thousand, and so forth. For instance, 632 is 600 when rounded to the nearest hundred because it is much closer to 600 than 700.
Rounding to the Nearest Tenth
When rounding numbers to the nearest ten, we must immediately look at the one place, the digit, to the right of the tens. For instance, the result of rounding the number 5327 to the nearest ten is 5330.
Rounding to the Nearest Hundredth
When we round numbers to the nearest hundred, we must look at the tens place, the digit immediately following the hundreds place. For instance, 9756 becomes 9800 when rounded to the nearest hundred.
Rules For Rounding Numbers in Approximation
A few fundamental guidelines must be adhered to when rounding numbers.
- We must first determine our rounding number. This is the number that will be affected in the end.
- Following that, we must examine the digit to the right of this location, determining the fate of the rounding digit.
- We do not change the rounding number if the number to the right is less than 5. However, all numbers to the right of the rounding number are changed to 0.
- If the digit to the right is five or greater, the rounding digit is increased by one, and all values to the right of the rounding number are changed to 0.
Approximation of Decimal Numbers
A decimal number has two parts: a fractional part and a whole number separated by a decimal point. Rounding decimal numbers is similar to rounding real numbers, with the exception that we must know the decimal place values of all digits in the given number. This includes both the digits preceding and following the decimal point.
To express the place values after the decimal point, we commonly round decimal numbers to the nearest tenths, hundredths, and thousandths. However, sometimes we must round a decimal number to the nearest whole number.
We check the tenth digit in this case. If it is equal to or greater than 5, the given number is rounded up; if it is less than 5, the given number is rounded down.
For example, if we approximate the number 6.69 to the nearest whole number, the number in the tenth place is 6. The decimal number can then be rounded to 7. We can write the equation as 6.68 $\approx$ 7.
Approximation With Examples
The following examples will show us how we approximate numbers.
Example 1
Approximate the number 2340 to the nearest hundred value.
Solution
We can approximate the number 2340 to the nearest hundred value easily. First, we need to determine the hundredth value, 3. Now looking at the number on its right, we see it is 4. As four is less than 5, we must round down the number. After we round down the number, we get 2300 as the answer. The approximation can be written as the following:
2340 $\approx$ 2300
Example 2
Approximate the decimal number 34.56 to the nearest tenth number.
Solution
The decimal number 34.56 needs to be approximated to the nearest tenth. The first value after the decimal point is called the tenth or first decimal place; the number is 5. Now we look at the number adjacent to 5, which is 6. As the number exceeds 5, we will round up the decimal number to 6.
The approximation would be 34.6. We can write the expression as follows:
34.56 $\approx$ 34.6
Example 3
Approximate the decimal number 3.255 to the nearest hundredth place.
Solution
It is necessary to round the decimal number 3.255 to the nearest hundredth or two decimal places. The second decimal place, or hundredth, is the number that comes after the decimal point and is equal to 5. We now examine the number 5, which is immediately adjacent to 5. We will round the decimal number to 6 because it is 5.
The approximation would be 3.26. The expression can be expressed as follows:
3.225 $\approx$ 3.26
All images/tables are made using GeoGebra.
