Apothem|Definition & Meaning

To measure the apothem of a regular polygon, find the midpoint of one of its sides and measure it from the center of the polygon. A segment as well as a unit of measurement in one. Regular polygon area calculation is the most common application of this method. The sides of a regular polygon are all the same length, and the polygon itself is closed. In regular polygons with congruent sides, apothems do not exist. 

The following figure represents the apothem of different polygons.

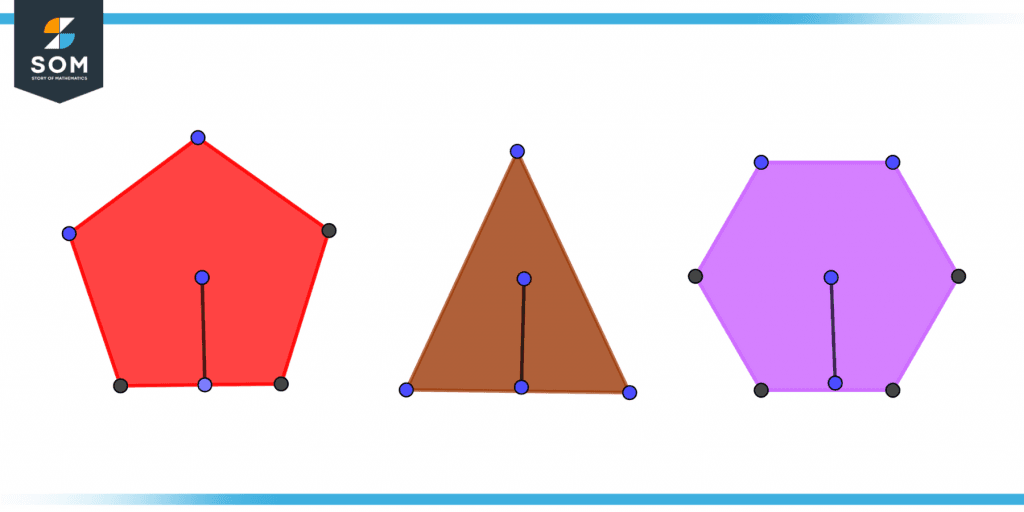
Figure 1 – Apothem of different polygons

The apothem functions as both the center and the radius of an incircle that constitutes the polygon. There are n different apothems for a polygon that has n sides, with each side having an equal length of the course. The term “apothem” can be used to refer to either the line itself or to the distance that line covers.

Therefore, it is possible for you to appropriately say “draw the apothem” and “the apothem is 4 centimeters.”

Finding a Polygon’s Apothem: The Step-by-Step Guide

In the process of estimating the area and perimeters of polygons, apothems can be of great use. Finding the apothem of a polygon requires sufficient information, which may be obtained by knowing its perimeter and area. The procedure for determining a polygon’s apothem is shown below.

To begin, let’s look at the formula for calculating the area of a polygon:

A = 0.5 x a x p

Multiplying “2” on both sides results in:

2 x A = a x p

Dividing “p” on both sides results in:

(2A)/p = a

• Where the polygon area is represented by A.
• The polygon perimeter is represented by P.
• “a” represents the apothem.

What Is Apothem Used For?

According to the following formula, the apothem a can be used to determine the area of any regular n-sided polygon with side length s. The formula furthermore states that the area is equivalent to the apothem calculated by multiplying by half the perimeter because ns = p. You can use this information to calculate the area of any regular n-sided polygon. A normal polygon will always have an apothem that is a radius of the circular circle.

How To Calculate Apothem Length

There are situations where a regular polygon’s area is unknown and just its side lengths are known. Another apothem formula could be applied here:

apothem = $\displaystyle\frac{s}{2\tan \left( \frac{180}{n} \right)}$

• The regular polygon’s side length is denoted by the letter s.
• While n represents the number of sides of the polygon.

What Exactly Is the Distinction Between an Apothem and a Radius?

In a regular polygon, the radius travels from the center of the shape to each vertex, where it cuts the angle formed by the vertex in half. The apothem extends in a straight line from the central point to the middle of each side. The side is always cut in half by it, and it always runs perpendicular to the side.

What Accounts for the Fact That the Radius Is Larger Than the Apothem?

In a regular polygon, the apothem is the larger leg of the right triangles created from the isosceles triangles, and the hypotenuse is the part of the triangle that corresponds to the radius. As a consequence of this, the radius is larger than the apothem.

Apothem’s Visual Portrayal

The graphic below depicts a visual representation of a polygon with seven sides and shows its apothem.

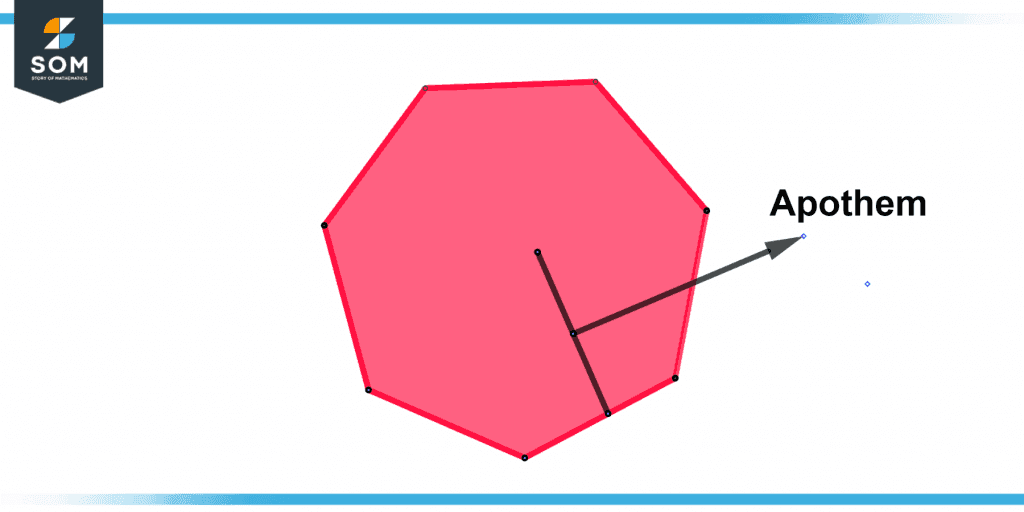
Figure 2 – Visual representation of an apothem for seven side polygon

Figure 3 shows two polygons of different sides which displays the visual representation of apothem.

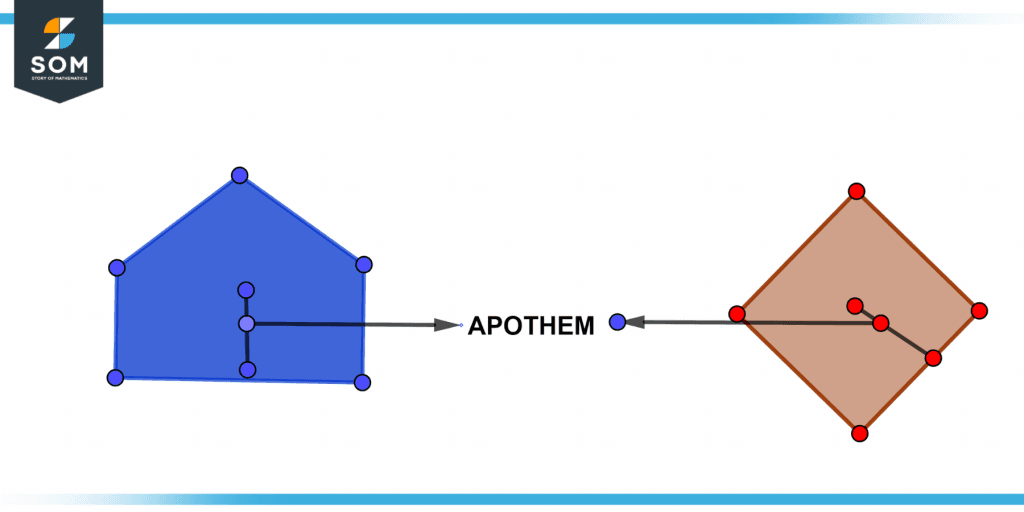
Figure 3 – Apothem for two different polygons

Numerical Examples for Apothem

Example 1

Figure out the area of a polygon that has an apothem of equal 5 feet and a perimeter that has a value of 12 feet.

Solution

We know that :

A = 0.5 x a x p

• Where the polygon area is represented by A.
• The polygon perimeter is represented by P.
• “a” represents the apothem.

Given that:

Apothem = 5 feet

Perimeter = 12 feet

By putting values, we get:

A = 0.5(5)(12)

A = 0.5 x 60

A = 30 sq. ft.

Thus the area of the polygon is 30 sq. ft.

Example 2

Figure out the area of a polygon that has an apothem of equal 5 feet and a perimeter that has a value of 48 feet.

Solution

We know that :

A =0.5 x a x p

• Where the polygon area is represented by A.
• The polygon perimeter is represented by P.
• “a” represents the apothem.

Given that:

Apothem = 5 feet

Perimeter = 48 feet

By putting values, we get:

A = 0.5(5)(48)

A = 0.5(240)

A = 120 sq. ft.

Thus the area of the polygon is 120 sq. ft.

Example 3

What’s the apothem for a regular polygon with a 204 square unit area and a 75 unit perimeter?

Solution

Given that :

Area of polygon = 204 square unit

Perimeter = 75 units.

We need to find the apothem. We know that:

A = 0.5 x a x p

• Where the polygon area is represented by A.
• The polygon perimeter is represented by P.
• “a” represents the apothem.

Rearranging the above formula results in the following:

a = (2A)/p

By putting values, we get:

a = 2(204)/75

a = 408/75

a = 5.44

Thus the apothem for the given data is 5.44.

Example 4

Think about the heptagon in the figure, whose sides are each 4 units long. Can you tell me the apothem of a polygon?

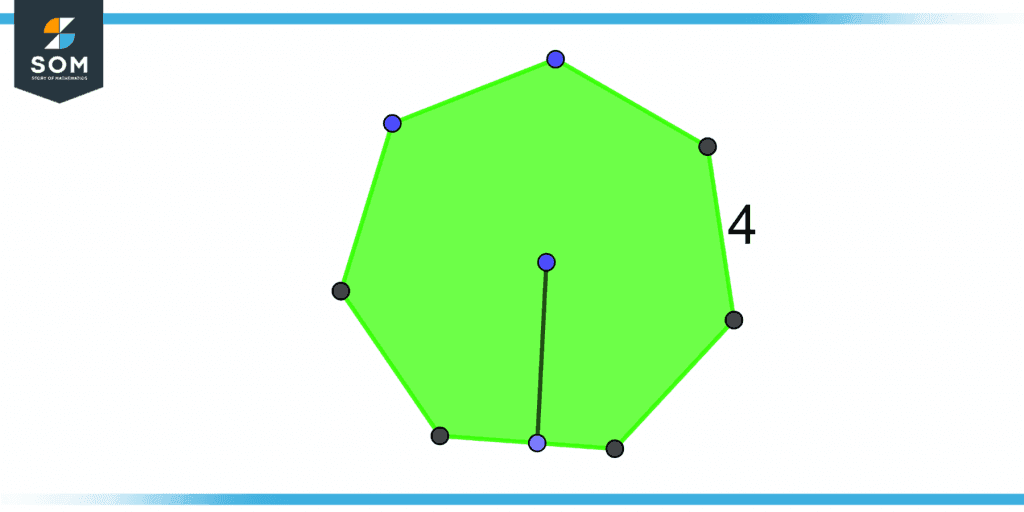
Figure 4 – Heptagon

Solution

Given that:

Size length = 4 units

No of sides = 7

We need to find the length of the apothem. We know that:

apothem = $\displaystyle\frac{s}{2\tan\left( \frac{180}{n} \right)}$

• The regular polygon’s side length is denoted by the letter s.
• While n represents the number of sides of the polygon.

By putting values, we get:

a = $\displaystyle\frac{4}{2\tan \left(\frac{180}{7}\right)}$

a= $\dfrac{4}{2\tan (25.71)}$

a = $\dfrac{4}{2(0.48)}$

a= $\dfrac{4}{2(0.48)}$

a = $\dfrac{4}{0.96}$

a = 4.153

Thus the length of apothem for the given data is equal to 4.153.

All images/mathematical drawings were created with GeoGebra.

Apex Definition < Glossary Index > Approximation Definition