JUMP TO TOPIC
Apex|Definition & Meaning
Definition
An apex, in geometry, is the vertex that is at the most heightened point of a certain shape. The term is generally used to direct to the vertex opposite to the base. The phrase Apex is taken from the Latin for peak, summit, tip, extreme end, and top.
An apex is the most heightened juncture of certain shapes. Mount Everest’s apex is the peak of the mountain. The apex is usually found at a vertex. A vertex is a single point where two or more lines, curves, or sides meet. The apex is found right at the highest point over or opposite the underside of the body called a base.
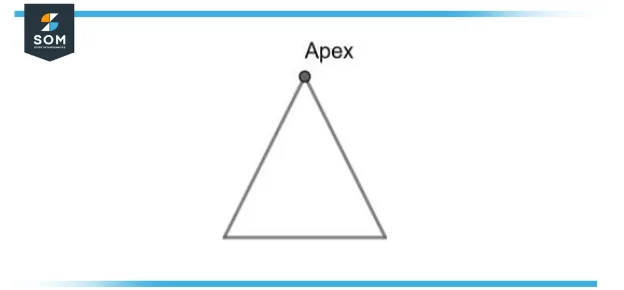
Figure 1 – Apex in Isosceles Triangle
The highest point on the earth is Mount Everest, at the evaluation of 29,000 feet. People who reach the top of mount Everest, reach the most heightened point on the earth. The apex of the earth is the peak of Mount Everest.
Apex in Isosceles Triangles
An apex is the most elevated point of a certain 2D and 3D figure relative to the base of a figure. Additionally, the phrase apex is usually used to direct to the most heightened vertex opposite to the base of a geometric figure. Below are some illustrations of geometric figures and their respective apex:
Apex in an isosceles triangle shown in figure 1 is the vertex where the two sides of the same size meet, opposite the base that is the unequal third side. The isosceles triangle’s vertex having an angle distinct from the two identical angles is called the isosceles triangle’s apex.
A triangle that has a minimum of two sides of equal length is called an isosceles triangle. Sometimes it is defined as having strictly two sides of equal length, and sometimes as having a minimum of two sides of the same length. The two equal sides are named the legs and the third side is named the triangle’s base. The other parameters of the triangle, like its area, height, and perimeter can be estimated by easy formulas from the measurements of the legs and base. The two angles opposite the legs are similar and acute.
Apex in Cone
The apex in a cone or pyramid is the vertex at the top which is opposite the base. The geometric shape of a cone is three-dimensional and it tapers smoothly from a balanced base to a point known as the apex.
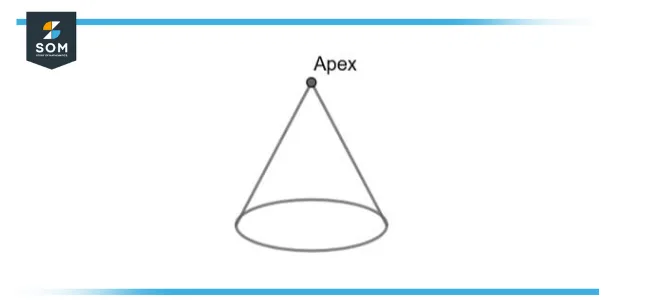
Figure 2 – Apex in Cone
A cone is constructed by a set of line segments. The lines join a shared point, the apex which is opposite to the base. The base may be limited to a circle, a quadratic form of any one-dimensional in the plane, or any one-dimensional closed figure, If the enclosed points are incorporated in the base, the cone is a solid entity, otherwise, it is a two-dimensional entity in a three-dimensional span. In the case of a solid object, the border formed by these lines is anointed as the lateral surface and it is said to be a conical surface if the lateral surface is unbounded.
In line segments, the cone does not spread beyond the base whereas in the case of lines, the cone spreads infinitely away in both directives from the apex, in which case it is occasionally named a double cone.
Apex in Pyramid
The apex of a right pyramid is directly above the centroid of its base. The base of a regular pyramid is like of a regular polygon and is usually insinuated to be a right pyramid.
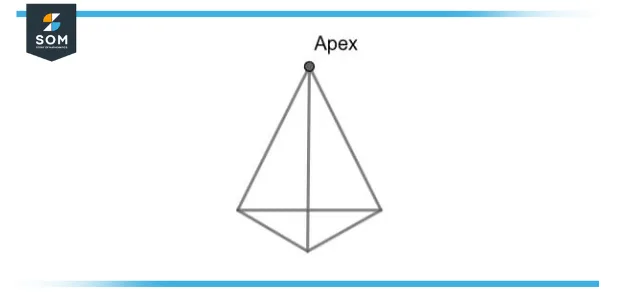
Figure 3 – Apex in Pyramid
A pyramid in geometry is a polyhedron composed by joining a polygonal base and a point, named the apex. Per apex and base edge form a triangle named a lateral face. It is a conic entity with a polygonal base. an n-sided base of a pyramid has n + 1 vertices, 2n edges, and n + 1 faces.
When unidentified, a pyramid is commonly assumed to be a standard square pyramid, like the physical pyramid designs. A tetrahedron is a name often given to the triangle-based pyramid. A pyramid is named acute if its apex is over the interior of the base and if its apex is over the exterior of the base then it’s called obtuse. The apex of the right-angled pyramid is over a vertex or edge of the base.
Height in Apex
The figure’s apex is usually associated with the height of the figure. The peak of a figure can be typically defined as the perpendicular length from the base of the figure to the flank opposite the base. If the figure has the apex, the peak of the figure is the perpendicular length from the apex to the base of the figure.
Hence, when a figure has an apex, the extreme peak of the figure contains the apex of the figure, but the apex just defines the highest juncture, while the peak is a measurement of distance.
Solving Apex: An Example
Does the apex exist in the prism shown below?
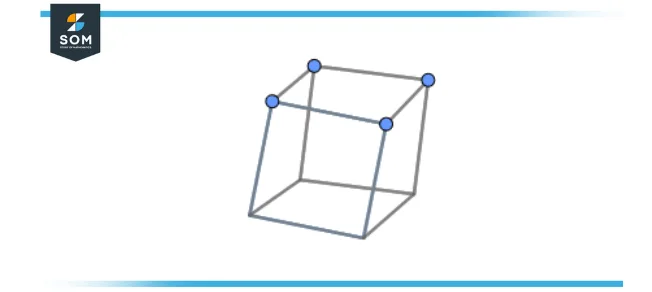
Figure 4 – Prism
Solution
No, the apex of such geometric figures does not exist. The explanation is, the phrase apex is only used to define particular geometric figures. The above geometric figure has multiple points to be viewed at an apex. Thus, the phrase apex is only and truly used in geometric figures like triangles, cones, pyramids, and other figures in which there is solely one most heightened vertex opposite the figure’s base. Otherwise, it would not be obvious what point is being directed to as the apex.
In the rectangular prism shown above, we could technically direct to four different points opposite to a base as an apex. The red points in the figure symbolize four apices of the cube. Also, each of the four points in the figure has the exact same height as any juncture on the face of the prism opposite the desired base, so none of the apices would hold the description of being the most elevated point, since they would all be the most elevated point of the prism.
All images/graphs are created using GeoGebra.
