JUMP TO TOPIC
Annual Percentage Rate APR|Definition & Meaning
Definition
The annual interest produced by a sum that is paid to investors or charged to borrowers is referred to as the annual percentage rate (APR). APR is a percentage that expresses the actual annual cost of borrowing money throughout the course of a loan or the revenue from an investment.
An interest rate is written as an annual percentage rate. It factors in variables like monthly payments to determine what proportion of the principal you’ll pay annually. The annual percentage rate, or APR, is the rate of interest charged on investments that are not adjusted for interest that has accrued during the year.
The interest rate and annual percentage rate can be easily understood with the help of the following graphs.
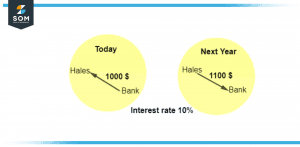
Figure 1 – Visual explanation of interest rate over a year.
Figure -1 shows that Hales borrows 1000 dollars from a bank today and banks say that the interest rate is 10 percent over a year so next year He has to 1100 dollars to the bank.
How to Calculate the Annual Percentage Rate (APR)
The annual percentage rate (APR) is determined by multiplying the interest rate for each period by the total number of periods in a year to which the interest rate was applied. The number of times the rate is really applied to the amount is not stated. Mathematically, it is calculated as:
APR = ((I + F/ P or LA) / N)) x 365 x 100
Where I represent Interest which is the sum of all installment payments paid over the course of the loan. The P represents the amount a person really borrows is known as the principal. At the conclusion of the borrowing, they must repay it. N is the loan term’s daily count. Fees may be equal to other costs, including transaction costs.
Different Types of Annual Percentage Rates
The two main types of APR are fixed and variable. A fixed APR does not change in reaction to changes in an index, in contrast to a variable APR. While this does not guarantee that interest rates will never change, it does mandate that the issuer give advance notice to the public. Variable APRs also referred to as variable-rate APRs, change in accordance with the index interest rate.
APR is typically a decent indicator of a loan’s cost. For instance, taking out a personal loan with high-interest rates can be demanding. If the loan is for a sizable sum, it is best to find out how much it would cost before deciding whether to accept it or not. This is due to the fact that in addition to the principal, the person must also pay the APR. Sometimes lenders will advertise low-interest rates to entice customers, but the additional fees may be quite taxing financially. This is sometimes especially true when it comes to mortgage annual percentage rates.
Understanding the Annual Percentage Rate Graphically
The following figure visually explains the concept of the annual percentage rate.
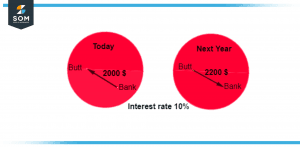
Figure 2 – 10% interest rate over a year
Figure 2 provides a graphic representation of a 10-percent interest rate applied to a $1,000 loan over the course of a year.
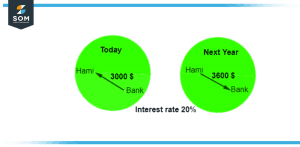
Figure 3 – Interest rate of 20 percent over a year
A loan of one thousand dollars with an annual interest rate of twenty percent is graphically represented in figure 3, which shows the progression of the loan over the course of one year.
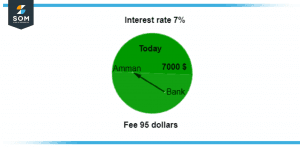
Figure 4 – Graphical representation of APR
Figure-4 shows the graphical representation of annual percentage rate where the total tenure is two year and loan interest are 700 dollars. The annual percentage rate in this case is 5.47 percent.
Numerical Examples for Annual Percentage Rate
Example 1
Consider taking out a $5,000 loan from a financial institution with a two-year term and a simple rate of interest of 5%. Over the course of the loan, you would pay $500 in interest. However, you were also charged a $75 origination fee.
Solution
The loan’s APR can be calculated in five steps:
Fees for origination and total interest charged added together:
75 + 500 = 575 dollars
Divide the answer from Step 1 from the principle, as appropriate:
575 / 5,000 = 0.115
Divide the outcome of Step two by the number of days remaining in the loan’s term:
0.115 / 730 = 0.00015753
Add 365 to the result from Step 3:
0.00015753 x 365 = 0.0575
To determine the APR percentage, multiply the Step 4 value by 100.
0.575 x 100 = 5.75%
Thus, the annual percentage rate is 5.75 percent.
Example 2
Consider Ali taking out a $16,000 loan from a financial institution with a two-year term and a simple rate of interest of 16%. Over the course of the loan, you would pay $1600 in interest. However, you were also charged a $185 origination fee.
Solution
The loan’s APR can be calculated in five steps:
Fees for origination and total interest charged added together:
185 + 1600 = 1785 dollars
Divide the answer from Step 1 from the principle, as appropriate:
1785 / 16000 = 0.111
Divide the outcome of Step two by the number of days remaining in the loan’s term:
0.111 / 1095 = 0.000101
Add 365 to the result from Step 3:
0.000101 x 1095 = 0.110595
To determine the APR percentage, multiply the Step 4 value by 100.
0.110595 x 100 =11.05%
Thus, the annual percentage rate is 11.05 percent.
Example 3
Think about Amman taking out a $7,000 loan from a bank with a two-year term and a 7% basic interest rate. You would pay interest on the loan totaling $700. You have also assessed an origination fee of 95 dollars, however.
Solution
The loan’s APR can be calculated in five steps:
Fees for origination and total interest charged added together:
95 + 700 = 795 dollars
Divide the answer from Step 1 from the principle, as appropriate:
795 / 7000 = 0.11
Divide the outcome of Step two by the number of days remaining in the loan’s term:
0.11 / 730 = 0.00015
Multiply 365 by the result from Step 3:
0.00015 x 365 = 0.05475
To determine the APR percentage, multiply the Step 4 value by 100.
0.05475 x 100 = 5.47%
Thus, the annual percentage rate is 5.47 percent.
All mathematical drawings and images were created with GeoGebra.
