Angle of Elevation|Definition & Meaning

What Is the Angle of Elevation? 

To understand height and distance, we need to begin with the most fundamental component, which is the “elevation angle” and the “angle of depression.” The angle of elevation of an item is termed as the angle between the horizontal and the axis that extends from the object to the eye of the observer. This angle is measured in degrees. The line along which an observer’s eyes are located is the sight line for that location.

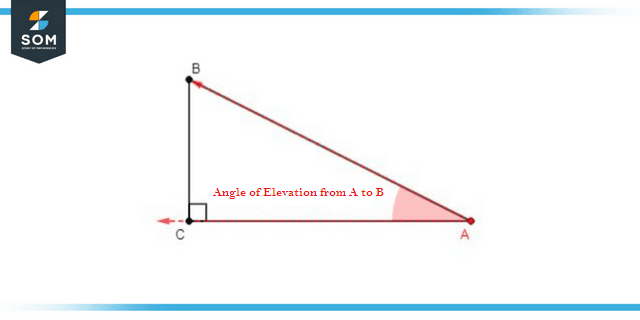
Figure 1: Angle of Elevation from A to B

Terms for Angle of Elevation

The three terms for the angle of elevation are discussed below:

Angle

The point at which 2 different rays or two line segments intersect at a common endpoint is termed the vertex of the intersection. When two parallel lines converge at a single point, this is known as the formation of an angle. Angles play a significant part, and some other explanations of angles include the following:

An angle is formed when a break, or gap, between two lines that join on one side.

The degrees serve as the unit of measurement for the angles.

Horizontal Line

It is a line parallel to the coordinate plane with no bends or kinks such that every point’s ordinate (or y-coordinate) is the same. The intersection of the angle and the horizontal line forms the elevation angle.

Line of Sight

The term “line of sight” refers to the imaginary line that may be drawn from the observer’s eyes to the point on the object that is being looked at directly. In this case, the object is positioned out of the observer’s line of sight. If we accurately read the elevation angle, we will have no trouble estimating the distance or the height. Because the angle formed concerning the observer’s eye to the top of a structure or a tower produces an imaginary right triangle, and the height of the structure or tower is considered perpendicular to the triangle, we use trigonometric functions in this situation. This is because the angle formed for the observer’s eye to the top of a structure or a tower produces a right triangle.

The Formula for the Angle of Elevation

The formula for determining the elevation angle requires the user to have data such as the measurements of the side close to the right angle, the side opposite the right angle, and the hypotenuse. If both the distances from the item and its height are known, then we can use the following equation to find the angle of elevation:

The tangent of an elevation angle is the height of an object divided by its distance.

Comparison of the Elevation Angle and the Depression Angle

When compared to the angle of elevation, the angle of depression depicts precisely the opposite scenario. In this scenario, the observer is placed at a higher elevation than the object, and the item is positioned so that it is out of the observer’s line of sight.

If the object is kept just below the eye level of the viewer, then the angles produced between the horizontal line and the observer’s line of sight are called the angle of depression. This is how we may define the term “angle of depression.”

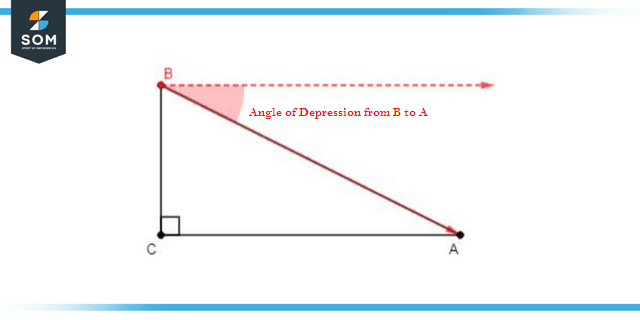
Figure 2: Angle of Depression from B to A

In summary, when the line of sight to an object points above the horizontal axis or plane, they create an angle of elevation. On the contrary, when the line of sight to an object points below the horizontal axis or plane, they form the angle of depression.

What Does the Angle of Elevation Look Like in a Triangle?

In a triangle, the angle generated between the hypotenuse and the horizontal leg is known as the angle of elevation. The following formula can be used to find the mathematical calculation of the angle of elevation:

The formula for calculating the angle of elevation is tan(-1) “opposite leg” / “adjacent leg.”

How To Calculate the Angle Formed by the Distance and Elevation?

Apply the following formula to determine the angle of height and distance:

The length of the opposite leg divided by the length of the adjacent leg is the formula for calculating the tangent of an angle of elevation. Enter the known numbers, and then proceed to solve for the value that is not known.

Solved Problems for Calculating Angles of Elevation

Example 1

A gardener is trying to water a 10ft heightened bush with the sprinkler nozzle. The nozzle is 4ft away on the ground from the bush and takes a straight projection. What is the angle of elevation of the gardener’s aim?

Solution

The bush height is 10ft, whereas the diagonal distance between the nozzle and the bush top is 4ft. The ground distance from the bush to the sprinkler can be determined using the Pythagoras theorem.

(Hyp)² = (Base)² + (Perpendicular)²

To Find the Angle of Elevation:

Tanθ = (Height of the bush) / (Diagonal Distance)

Angle of Elevation, θ =Tan-¹ (10/4)

= 68.19°

Example 2

After accurate measurements, it was found that when the sun is at 45°, the mango tree’s shadow becomes 15m in length. Find the height of the mango tree from the given data in the statement.

Solution

The statement mentions the diagonal distance of the shadow is 15m, whereas the angle is 45°. Using the tangent formula, we can easily find the height of the mango tree as follow:

The Formula: tanθ =    tan 45° = 1

15 x 1 = x

15m = x

Figure 3: Diagrammatic Representation of Example 2

The height of the mango tree is 15m, which is the perpendicular distance if considered in the sense of Pythagoras’ theorem.

All mathematical drawings and images were created with GeoGebra.

Angle Bisector Definition < Glossary Index > Annual Percentage Rate Apr Definition