Angle Bisector|Definition & Meaning

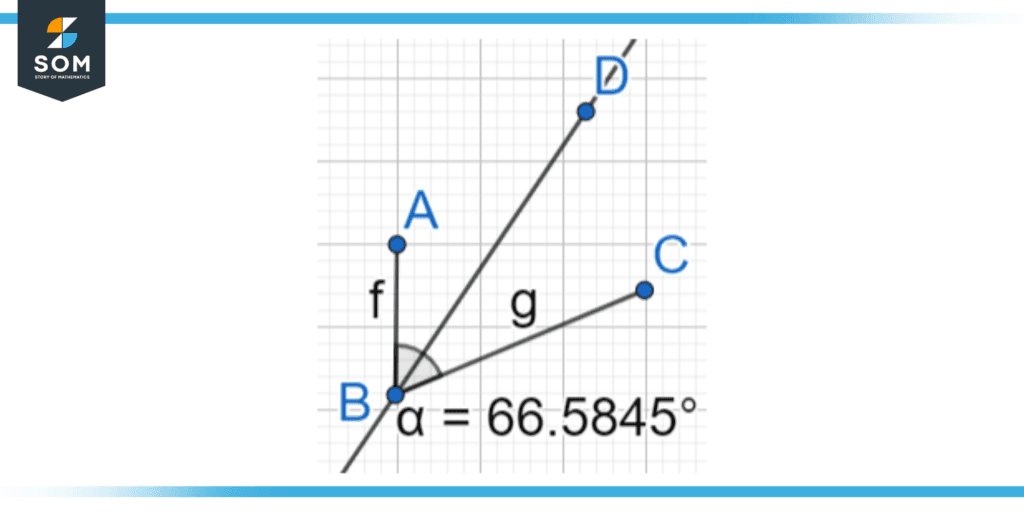
Figure 1: An angle bisecting line BD cutting an angle 66.58 into half made between the lines AB and BC. 

In general, a bisector that bisects means to cut into two halves. Here, we are cutting an angle into two halves by using an angle bisector crossing that angle through the center point (in the above case, the line BD is the angle bisector).

These bisectors are very handy in making smaller angles from larger angles that are already given. Let us say that we are given an angle of 60°, and we ideally want a smaller angle of 30°. All that we are required to do is draw that 60° angle between two lines and then draw an angle bisector between the two. This gives us two 30° angles to work around with. There are even further applications of an angle bisector that will be discussed later in this article. 

Properties of an Angle Bisector

An angle bisector is usually renowned for its properties that aid in the easy construction and organization of shapes and structures in many real-life applications. Firstly, an angle bisector can bisect any angle ranging from 0° to 360° (that is a whole circle). This means that any angle can be bisected into equal halves by an angle bisector. 

Furthermore, the points on the angle bisector are all equidistant to the two adjoining line segments of the respective bisected angle. This gives us a symmetrical shape and the two sides are mirror images of each other, which further aids in the geometrical constructions of many shapes.

Moreover, considering an angle bisector of one of the points of a triangle, it will cut the opposite side of the triangle into a ratio based on the ratio of arm length of the other adjacent sides of the bisecting angle point. This means that the bisecting line will not always cut the triangle in half and the bisected figure will not be symmetrical. 

Additionally, in a triangle, taking the angle bisector on all three vertices of a triangle results in an intersecting point on the triangle. This intersection denotes the center of the triangle and is called the incenter. 

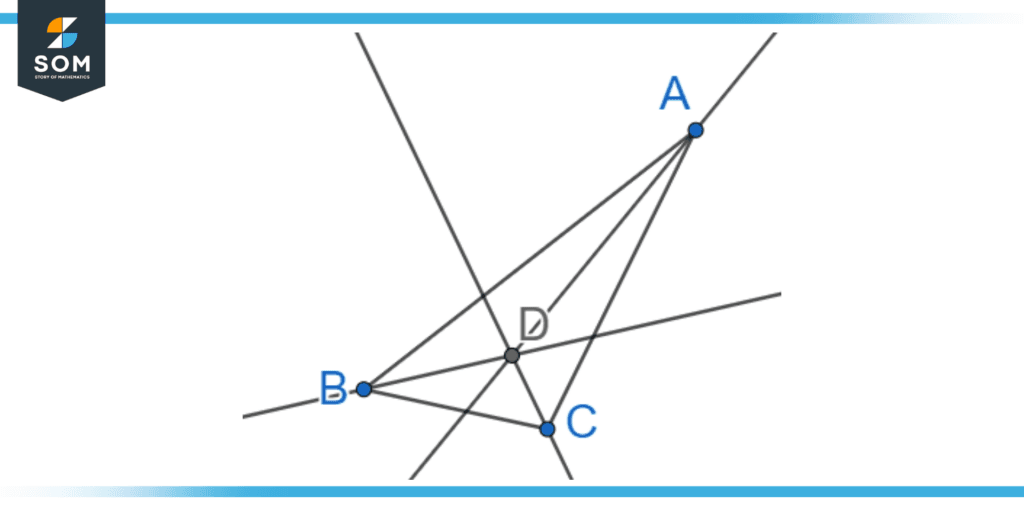
Figure 2: Point D shows the incenter of the triangle formed by the intersection of the three angle bisectors.

Similarly, to find a center of a circle geometrically, we can draw three tangential adjoined lines to make a triangle around it. Thus, by taking the three angle bisectors of the triangle, the intersecting point is the center of the circle.

Construction of an Angle Bisector

In today’s era of technological advancements, one can get his hand on any angle bisector constructing tool on the internet, which makes it easy for the common person to bisect any angle in half. Nevertheless, the geometrical construction on a piece of paper is very simple as well. All you need is graphing paper, a compass, a ruler, and a lead pencil.

Let us say we are given an angle ∠ABC made between the two adjoining line segments AB and BC. If needed, this angle can be measured using a protractor and can be halved as well using. But in real-life cases where we might not have a protractor in our hands at all times, we can use the compass to find its half.

Firstly, we open the compass at a fixed length for all times, and from the origin point, we draw two arcs that intersect the two line segments individually. After that, we place our pivoting arm of the compass on the intersection of one of the line segments and the arc to draw an arc towards the inside of the line segment. A similar procedure is followed for the other line segment.

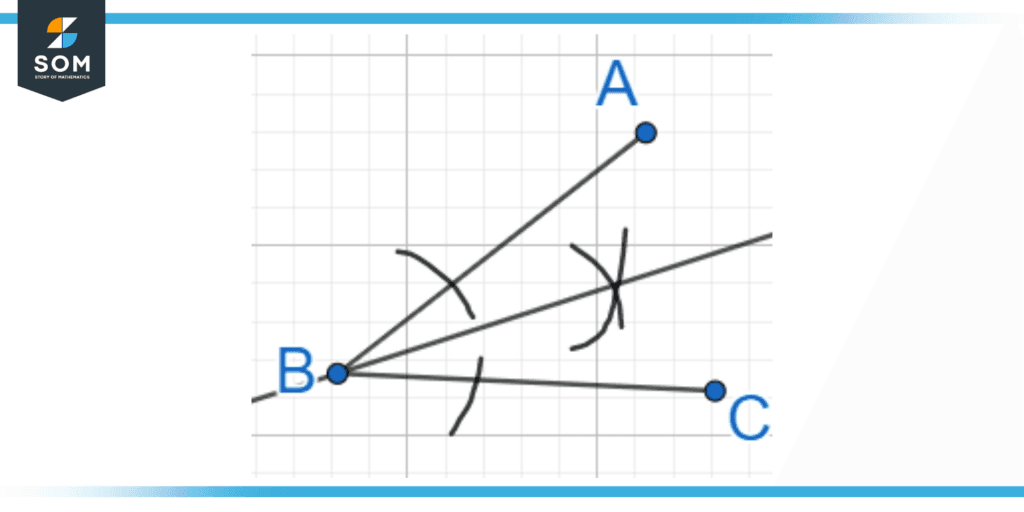
Figure 3: Arcs are drawn using a compass to find the angle bisector of the angle ABC

These arcs will intersect with one another and we can call this point D. Afterwards, we draw a line BD, using a ruler,  between points B and D. This line is the resulting angle bisector that will split the angle ∠ABC into half. Moreover, we have to place great emphasis on the opening of the compass which has to be kept the same throughout the construction of the angle bisector. 

Significance of the Properties of an Angle Bisector in Its Construction

This construction of the angle bisector utilizes one of the properties of the angle bisector which is equidistant from the two line segment at all points. Hence, the same points on the two line segments of a specific distance from the pivot point always have the same distance from the angle bisector.

Furthermore, the property that an angle bisector can be made for any angle is also true during its geometric construction using a compass where when we are given two line segments, it is always possible to construct an angle bisector regardless of the angle between the two adjoining line segment. 

Moreover, we can use the angle bisector theorem to find the length of the opposite side of the bisecting angle that is cut into two parts using the ratio of the adjacent sides of the angle.

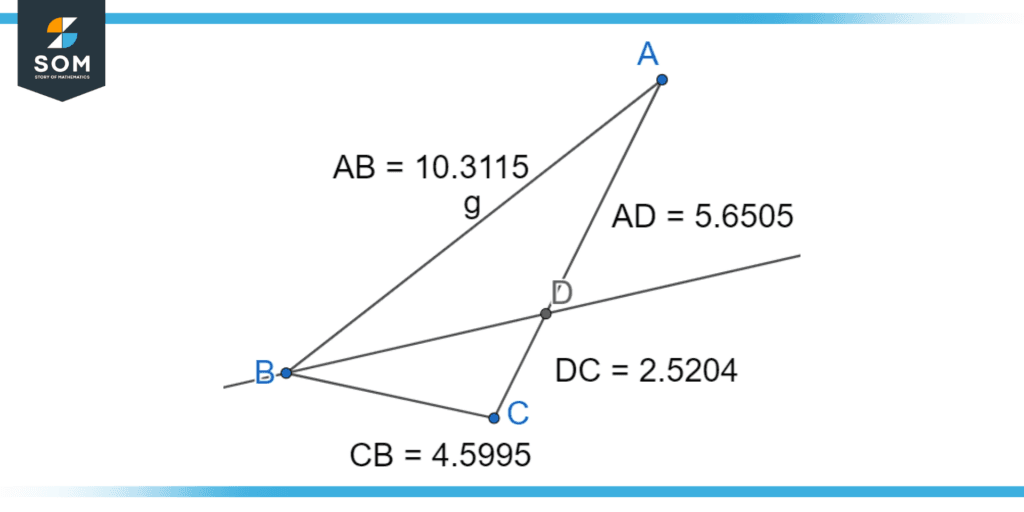
Figure 4: The visual representation of an angle bisector theorem.

In Figure 4, we can observe that the ratio between lines AB and BC is equal to the ratio between line AD and DC. This is known as the angle bisector theorem that is written as $\frac{AB}{BC} = \frac{AD}{DC}$

Further Explanation of an Angle Bisector Theorem Using an Example

Let us consider figure 4. We have a length of line AB = 10.3115 and the length of line BC = 4.5995. We are given a length of the line AD = 5.6505. Prove that the length of the line DC is equal to 2.5204 using the angle bisector theorem. 

Solution

Using the angle bisector theorem, we can find the length of AD by inputting the above-given values in the following equation: 

\[ \frac{AB}{BC} = \frac{AD}{DC} \]

\[ \frac{10.3115}{4.5995} = \frac{5.6505}{DC} \]

\[ \frac{(5.6505)(4.5995)}{10.3115} = DC \]

\[ \mathbf{DC = 2.5204}\]

Hence proven that the angle bisector theorem proves the above values are valid.

All mathematical drawings and images were created with GeoGebra.

And Definition < Glossary Index > Angle Of Elevation Definition