JUMP TO TOPIC
AND|Definition & Meaning
Definition
In Boolean logic, where the two states of a variable are either true (1) or false (0), AND is the Boolean operation that only produces a true state when all the Boolean variables involved are true.
In words, if two Boolean variables are A and B, then:
- If A and B are both true, A AND B is true
- If either one of A or B is false, A AND B is false
- If A and B are both false, AND B is false
Truth Table for AND
Consider the simple case of two Boolean variables A and B combined with the AND logic. If we represent the True and False states respectively as T and F, then the truth table for the Boolean statement A AND B is given below.
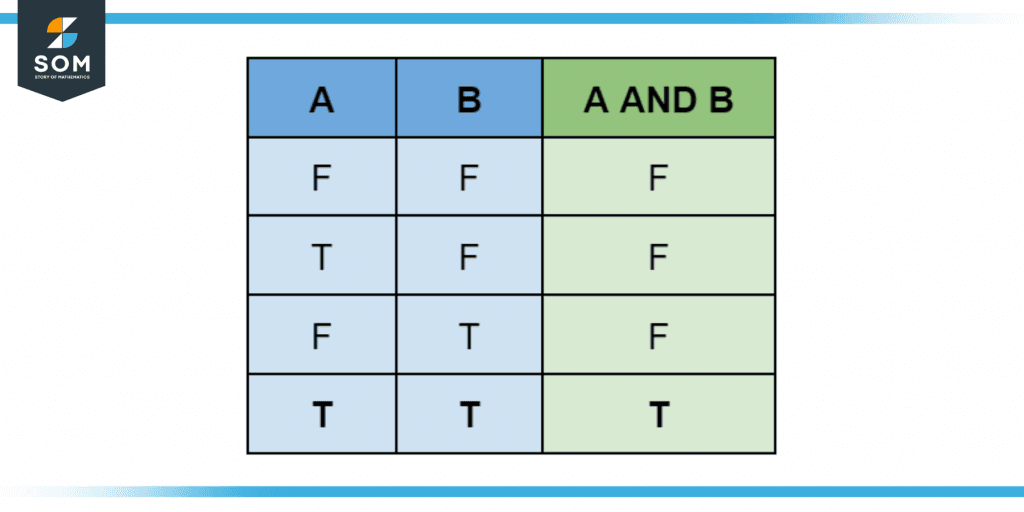
Figure 1 – Truth table two-variable AND.
Now let us add a third Boolean variable C. The output of AND is only true when all the inputs are true, so A AND B AND C is only true when all three inputs are true.
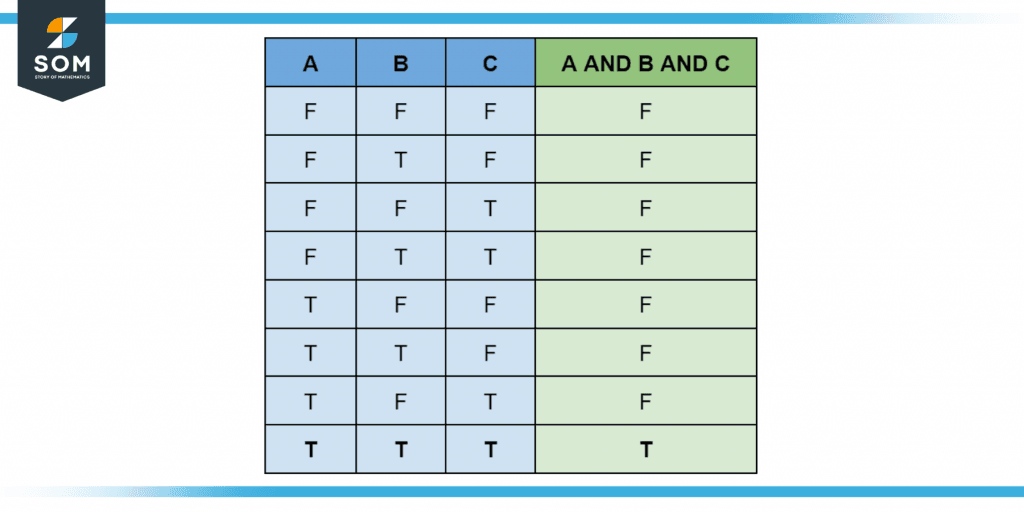
Figure 2 – Truth table for three-variable AND.
We can extend this to as many Boolean variables as we want quite easily. The key idea to remember is that AND operation will only produce a True state when all of them are true simultaneously.
Commutativity And Associativity
The logical AND is both commutative and associative. These properties allow us to write the following:
A AND B = B AND A
A AND (B AND C) = (A AND B) AND C
Here, the first statement shows the commutative property, while the second shows the associative property.
If you want to verify commutativity, simply swap the input columns in the first table, and notice that you end up with the same thing.
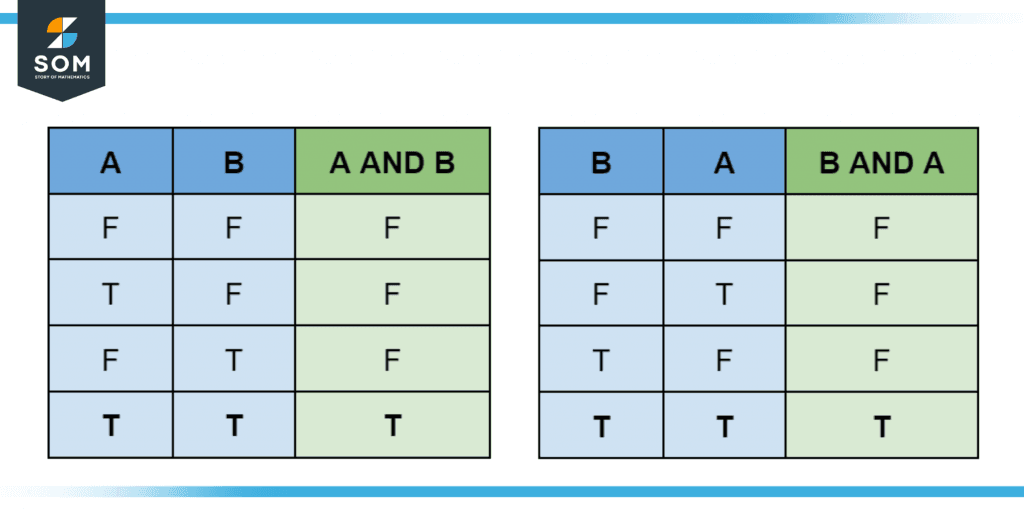
Figure 3 – Verifying the commutativity of the AND operation with a truth table.
The associative property, on the other hand, takes a little longer to verify.
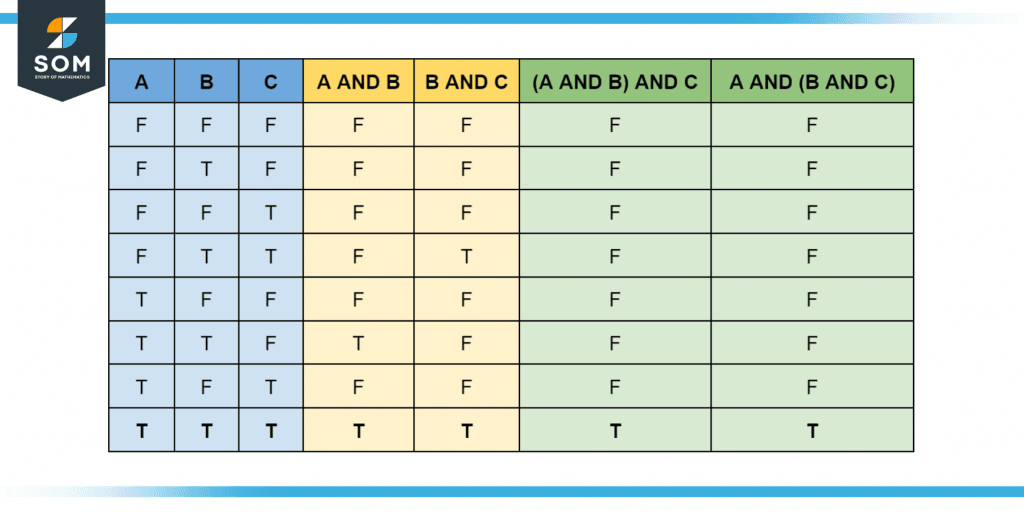
Figure 4 – Verifying the associative property of AND via a truth table.
As you can see, the associative property holds true.
Other Notations
You can think of logical AND as multiplication (* or $\cdot$) from arithmetic. It results in the equivalent product notation for AND: A $\cdot$ B, where $\cdot$ represents the AND operation. Using T = 1 and F = 0, then:
- 0 AND 0 = 0 $\cdot$ 0 = 0 * 0 = 0 or False
- 1 AND 0 = 1 $\cdot$ 0 = 1 * 0 = 0 or False
- 0 AND 1 = 0 $\cdot$ 1 = 0 * 1 = 0 or False
- 1 AND 1 = 1 $\cdot$ 1 = 1 * 1 = 1 or True
As you can see, this matches up with the truth table for AND. The familiar context of multiplication makes this notation an easy way to understand how AND works. However, remember many other logic operators (like XOR) are not that simple. Try to get comfortable with truth tables because they are the most effective way of describing logical operations!
Other symbols for AND include the wedge ($\boldsymbol\wedge$) and ampersand (&, usually in programming languages). For example, A $\wedge$ B and A & B both mean the same thing.
The intersection or conjunction of sets in set theory (denoted Set A $\boldsymbol\cup$ Set B) theoretically means the same thing as AND, but you will find that the wedge is the most common. Sometimes, the wedge is represented with ^ (usually used for exponentiation), though it understandably leads to confusion in contexts involving powers.
Explaining AND With Sets
In set theory, the conjunction or intersection of two sets can be represented as a logical operation as their meanings share a stark similarity. A $\boldsymbol\cup$ B is akin to A $\wedge$ B. Let us consider an example.
Assume we have one set A = {1, 2, 3, 4, 5} and another set B = {4, 5, 6, 7, 8}. Both sets have five numbers and share two of them, 4 and 5.
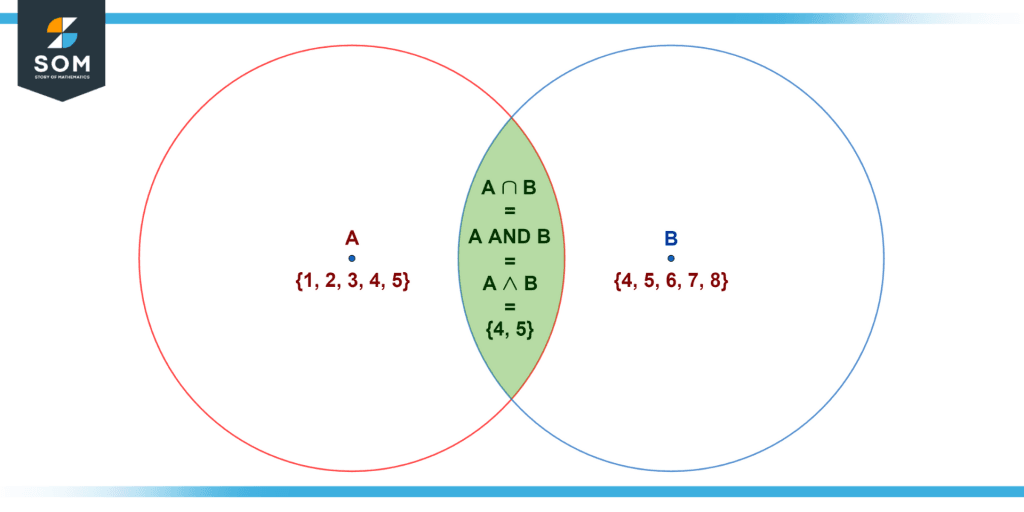
Figure 5 – The intersection of two sets can be represented with AND.
To find A $\boldsymbol\wedge$ B, we pick one of the sets, say A. Then, for each element of A, we check if the same element exists in B. For all those elements where this is true, we know they belong in the intersection of the two sets A and B!
We can extend the concept to any number of sets. Below, we give an example explaining the intersection of three sets and its relation to AND.
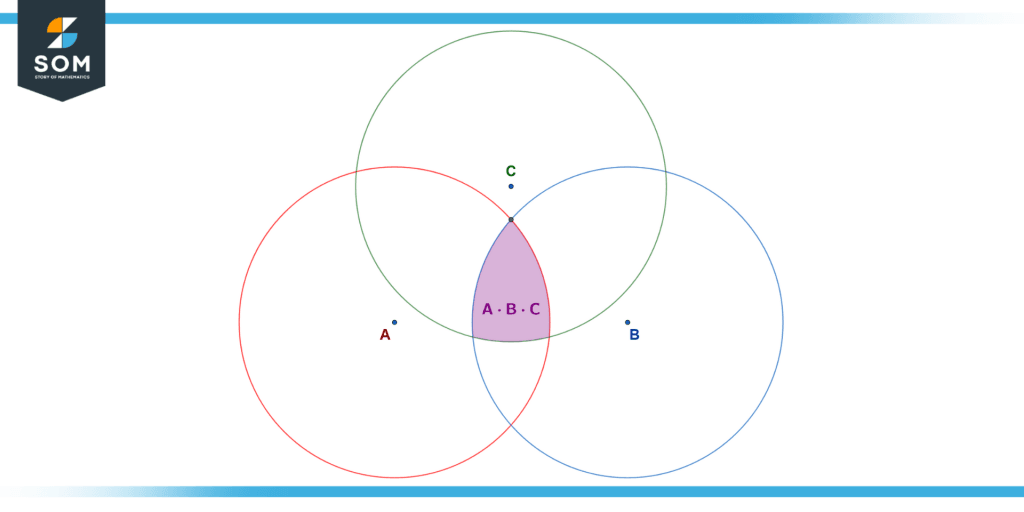
Figure 6 – The intersection of three sets (the purple-shaded region) can be represented with the AND operation.
Modeling Problems With AND in Real Life
Example 1
David needs to board the bus to school at 8:00 AM. Assuming the bus arrives exactly at 8:00 AM and leaves after five minutes at 8:05 AM, and David stays at home when he is sick, try to model the problem as a Boolean expression.
Solution
To model this, we identify two things. The first is that David needs to arrive at the bus stop no later than 8:05 AM. The second is that he must not be sick as he stays home otherwise. The two conditions are independent, meaning we can model them as separate Boolean variables A and B:
A = David arrives on time.
B = David is not sick.
Since both events must occur for David to board the bus, we use the logical AND:
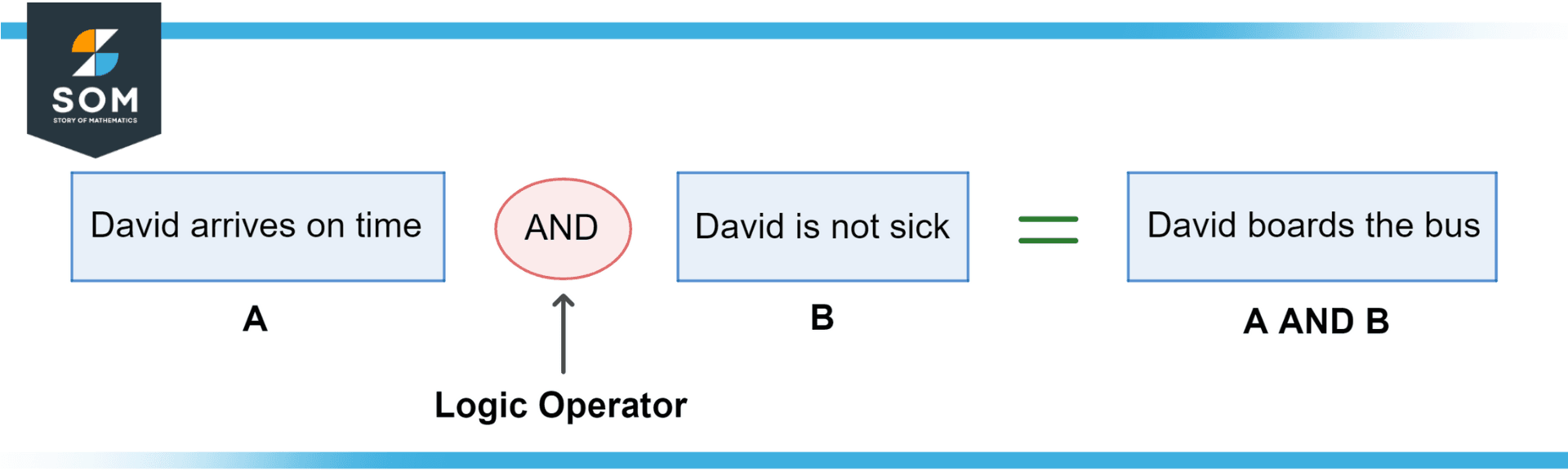
Figure 7 – A Boolean model for David successfully boarding the bus.
A AND B = David boards the bus.
Example 2
Consider the same scenario as before. Now assume the school’s transport department is having a problem and the bus occasionally might fail to arrive. Re-model the problem as a Boolean expression.
Solution
To remodel the problem, we consider the following variables:
A = David arrives on time.
B = David is not sick.
C = The bus arrives on time.
David boards the bus only when all these conditions are satisfied, so we can model it with the logical AND:

Figure 8 – The updated model from the first example for three boolean variables.
A AND B AND C = David boards the bus.
All mathematical drawings and images were created with GeoGebra.
