Analog|Definition & Meaning

Therefore, it refers to something tangible that is constantly changing. 

Description of Analog

The term analog is used mainly for signals. The analog signal represents the information in continuous form. The devices used for analog signals are called analog devices. In everyday situations, we use them everywhere.

We use the wave-based diagram below to illustrate the idea of an analog signal:

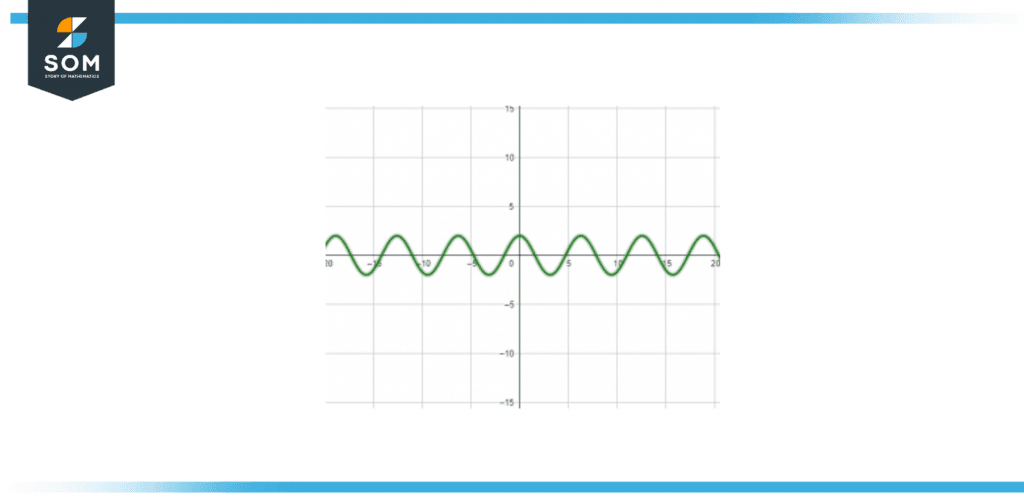
Figure 1 – Image of a wave-based diagram showing analog signal of  2cos(x)

Figure 1 shows the analog wave of cos(x) where the magnitude of this analog wave is 2.

Let us consider an example of an analog telephone. The human voice is transmitted across analog telephone lines as electrical impulses. The microphone on your phone transforms the sound waves into analog electrical waves whenever you talk into the device.

These waves go to their destination via the telephone line, which acts as their medium of propagation. The speaker in the receiving phone’s handset completes the process of converting the electrical impulses back into sound waves.

Information that is analog in its original form (such as audio and images) can display a continuous range of shifts in terms of intensity (such as loudness or luminance) and frequency. The analog electrical network converts the informational fluctuations in the native information stream into amplitude and frequency shifts in the carrier signal.

In other words, in order to produce an analog of the initial information stream, the carrier signal must be modulated, which means that its frequency is changed.

Amplitude modulation is a technique that allows for changes in the amplitude of electromagnetic sinusoidal (waveforms), often known as sine waves, while maintaining the same frequency (AM).

Alternately, a technique called frequency modulation can be used to alter the frequencies of the sine wave while keeping the amplitude the same (FM). In addition, it is possible to modify both the frequency and the amplitude at the same time.

A feature of the medium is used by an analog signal in order to communicate the information being sent by the signal.

Visual Explanation of Analog

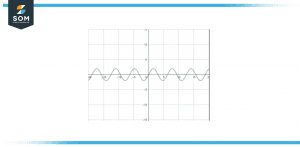
Figure 2 – Image of a wave-based diagram showing the analog signal of 2sin(x)

Figure 2 illustrates the analog wave that is produced by the function sin(x), where the magnitude of this analog wave is 2. The value of 2sin(x) is 0 at x equal to 0.

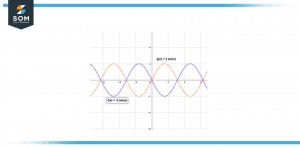
Figure 3 – Image of a wave-based diagram showing the analog signal of 2sin(x) and -2sin(x)

Figure 3 illustrates the sine wave produced by 2sin(x) and -2sin(x).

Numerical Problem of an Analog Function

The analog wave of 2sin(x) and 2cos(x) is shown below. You are required to find the following parts.

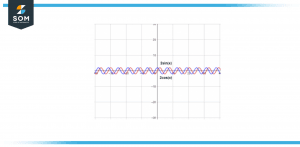
Figure 4 – Image of a wave-based diagram showing the analog signal of 2sin(x) and 2cos(x)

a) Find the value of 2sin(x) when the value of x is 2 and 0.

b) Find the value of 2sin(x) when the value of x is 4 and 0.

c) Find the value of 2sin(x) when the value of x is 6 and 0.

d) Find the value of 2sin(x) when the value of x is 8 and 0.

e) Find the value of 2cos(x) when the value of x is 2 and 0.

f) Find the value of 2cos(x) when the value of x is 4 and 0.

g) Find the value of 2cos(x) when the value of x is 6 and 0.

h) Find the value of 2cos(x) when the value of x is 8 and 0.

Solution

a) We have to find the value of 2sin(x) at x equal to 2 and 0.

So,

= 2sin(x)

At x equal to 2 results in:

= 2sin(2)

= 2 x 0.90929742682

= 1.81859485365

Now at x equal to 0 results in:

= 2sin(0)

= 2 x 0

= 0

Thus the value of 2sin(2) is 1.81859485365 and the value is 0 at 2sin(0).

b) We have to find the value of 2sin(x) at x equal to 4 and 0.

So,

= 2sin(x)

At x equal to 4 results in:

= 2sin(4)

= 2 x (- 0.7568024953 )

= – 1.51360499062

Now at x equal to 0 results in:

= 2sin(0)

= 2 x 0

= 0

Thus the value of 2sin(4) is – 1.51360499062 and the value is 0 at 2sin(0).

c) We have to find the value of 2sin(x) at x equal to 6 and 0.

So,

= 2sin(x)

At x equal to 4 results in:

= 2sin(6)

= 2 x (- 0.27941549819 )

= – 0.55883099639

Now at x equal to 0 results in:

= 2sin(0)

= 2 x 0

= 0

Thus the value of 2sin(6) is -0.55883099639 and the value is 0 at 2sin(0).

d) We have to find the value of 2sin(x) at x equal to 8 and 0.

So,

= 2sin(x)

At x equal to 4 results in:

= 2sin(8)

= 2 x (0.98935824662 )

= 1.97871649325

Now at x equal to 0 results in:

= 2sin(0)

= 2 x 0

= 0

Thus the value of 2sin(8) is 1.97871649325 and the value is 0 at 2sin(0).

e) We have to find the value of 2cos(x) at x equal to 2 and 0.

So,

= 2cos(x)

At x equal to 2 results in:

= 2cos(2)

= 2 x (-0.41614683654)

= -0.83229367309

Now at x equal to 0 results in:

= 2cos(0)

= 2 x 1

= 2

Thus the value of 2cos(2) is -0.83229367309 and the value is 1 at 2cos(0).

f) We have to find the value of 2cos(x) at x equal to 4 and 0.

So,

= 2cos(x)

At x equal to 4 results in:

= 2cos(4)

= 2 x (-0.65364362086)

= -1.30728724173

Now at x equal to 0 results in:

= 2cos(0)

= 2 x 1

= 2

Thus the value of 2cos(4) is -1.30728724173 and the value is 1 at 2cos(0).

g) We have to find the value of 2cos(x) at x equal to 6 and 0.

So,

= 2cos(x)

At x equal to 6 results in:

= 2cos(6)

= 2 x (0.96017028665)

= 1.9203405733

Now at x equal to 0 results in:

= 2cos(0)

= 2 x 1

= 2

Thus the value of 2cos(6) is 1.9203405733 and the value is 1 at 2cos(0).

h) We have to find the value of 2cos(x) at x equal to 8 and 0.

So,

= 2cos(x)

At x equal to 8 results in:

= 2cos(8)

= 2 x (-0.1455000338)

= -0.29100006761

Now at x equal to 0 results in:

= 2cos(0)

= 2 x 1

= 2

Thus the value of 2cos(8) is -0.29100006761 and the value is 1 at 2cos(0).

All mathematical drawings and images were created with GeoGebra.

Amplitude Definition < Glossary Index > And Definition