JUMP TO TOPIC
Amplitude|Definition & Meaning
Definition
Amplitude is defined as the height from the middle value of a periodic function to the maximum or the minimum value of the function. It is the height from the center of the periodic signal to the trough or the crest of a wave. It defines how much something is enhanced or amplified.
Illustration of Amplitude
Consider a periodic function y = sin 2x. The amplitude of this periodic signal is shown in figure 1.

Figure 1 – Amplitude Illustration of the periodic function y = sin 2x
The height AB or CD is the amplitude of the sine wave. Note that point A is the maxima or the peak value and point C is the minima or the crest of the sine wave.
Amplitude and Its Importance in Communication Systems
Amplitude is essential in communication systems where signals need to be projected over long distances.
The amplitude provides strength to the periodic signal. It is the height from the peak value or the crest to the center or the mean of a signal. The signal’s amplitude or strength changes by increasing or decreasing this height.
Calculation of Amplitude
Amplitude can be calculated by adding the positive values of the crest and the trough and then dividing by 2.
Attenuation
Attenuation means that the amplitude of the signal decreases whereas a booster increases the amplitude so that it can be carried out to its destination.
Amplitude in Angular Motion
A periodic signal can also be considered as a circle when discussing angular motion. The radius of the circle is the amplitude of the periodic signal. The circle’s radius decreases or increases by amplitude.
Amplitude and Other Terminologies
In communication systems, the amplitude of the signal is accompanied by some other terminologies which cannot be left out while dealing with the amplitude of a signal.
These are such important as the amplitude of the function. These terms are time period, frequency, and wavelength.
All these terms define a complete set of properties for the periodic function. It is also necessary to understand a periodic function before discussing its amplitude.
The periodic function and the terms such as time period, frequency, and wavelength are defined as follows:
Periodic Function
A periodic function is defined as a signal with repeating values of the function after regular intervals. The value of the function recurring after equal time intervals defines the periodicity of the function.
Periodic functions play an important role when dealing with terms such as amplitude, time period, frequency, and wavelength.
A non-periodic function has varying values of these terms as the signal’s values are continuously changing. They do not repeat after the same time intervals thus they can’t have constant amplitude, frequency, or wavelength.
Time Period
The time period is the time the signal takes to complete one cycle. A wave cycle involves a maximum value and the minimum value of the signal, after which it drops to its recurring value.
The time period is measured in seconds and has an inverse relation with the frequency of the periodic function. The mathematical formula for the time period relating to the frequency is as follows:
T = 1/f
Where T is the time period and f is the frequency.
Consider figure 2 for the time period for the particular sine wave. The time period is the time interval denoted by T.

Figure 2 – Time Period Illustration of the function y = sin 2x
Note that the function’s value is the same at both ends of the time interval and inhibits a complete cycle.
Wavelength
The wavelength is the distance between two successive troughs or two crests in the two adjacent cycles of the signal. It is the distance between two same points from one cycle to the next.
The wavelength is measured in meters and is represented by the greek letter lambda λ. It is inversely proportional to the frequency of the wave.
Consider figure 3 for the wavelength illustration. The distance PQ from crest to crest is the wavelength of the particular sine wave.

Figure 3 – Wavelength PQ of the function y = sin 2x
Frequency
The number of waves passing through a fixed point in a specific time interval is called the frequency. The frequency defines the oscillations that occur per second in a periodic signal.
The mathematical formula relating frequency and wavelength is as follows:
c = f λ
Where c, f, and λ are, respectively, the speed of light, the frequency, and the wavelength. The frequency is measured in Hertz (Hz) or per second.
Consider figure 4 for the frequency of the sine wave. The number of wave cycles passing through a point M highlighted in the figure in one second is the frequency.

Figure 4 – Frequency Illustration for y = sin 2x through the point M
It could be any point as it is just a reference point.
Example of Altitude in Waves
Consider the periodic function y = 5 sin x as shown in figure 5. Calculate the periodic function’s amplitude, wavelength, frequency, and time period.
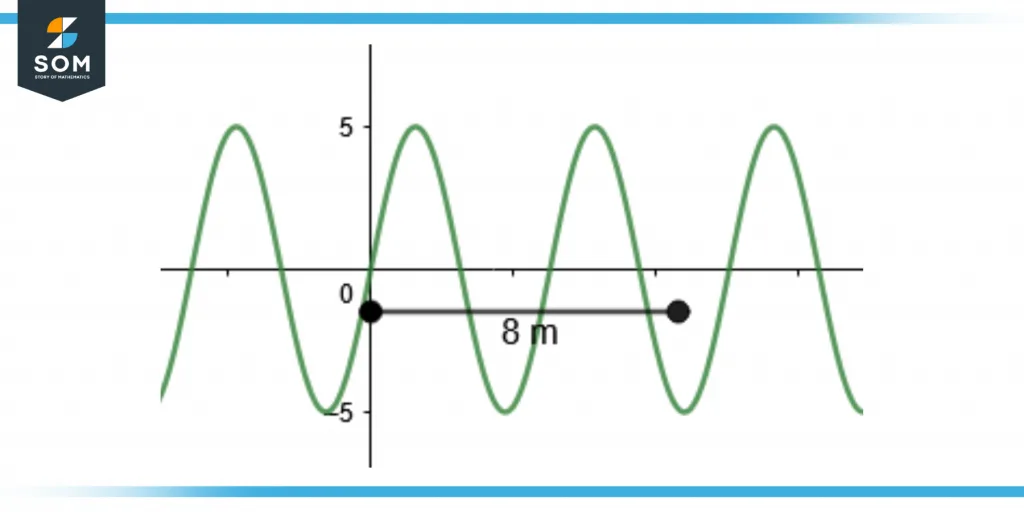
Figure 5 – Periodic Function y = 5 sin x
Solution
The figure shows the trough of the sine wave at 5 and the crest is at -5. The amplitude can be calculated by adding the crest and trough values and dividing the result by 2.
As the amplitude is a height, the crest value is taken as positive. So, the amplitude will be:
Amplitude = (5 + 5) / 2 = 10 / 2 = 5
The figure also shows the distance of 8 m between two wave cycles. The wavelength can be calculated by dividing it by 2 as it is the distance between two successive troughs or crests.
So the wavelength will be 4 meters.
The frequency can be calculated by using the formula c = f λ. The frequency will be:
\[ \text{f} = \frac{c}{λ} = \frac{ 3 × 10^{8} }{ 4 } = 7.5 × 10^{7} \ \text{Hz} \]
The time period can be calculated as follows:
\[ \text{T} = \frac{1}{f} = \frac{1}{ 7.5 × 10^{7} } = 1.33 × 10^{-8} \ \text{sec} \]
All the geometrical figures are created using GeoGebra.
