Average|Definition & Meaning

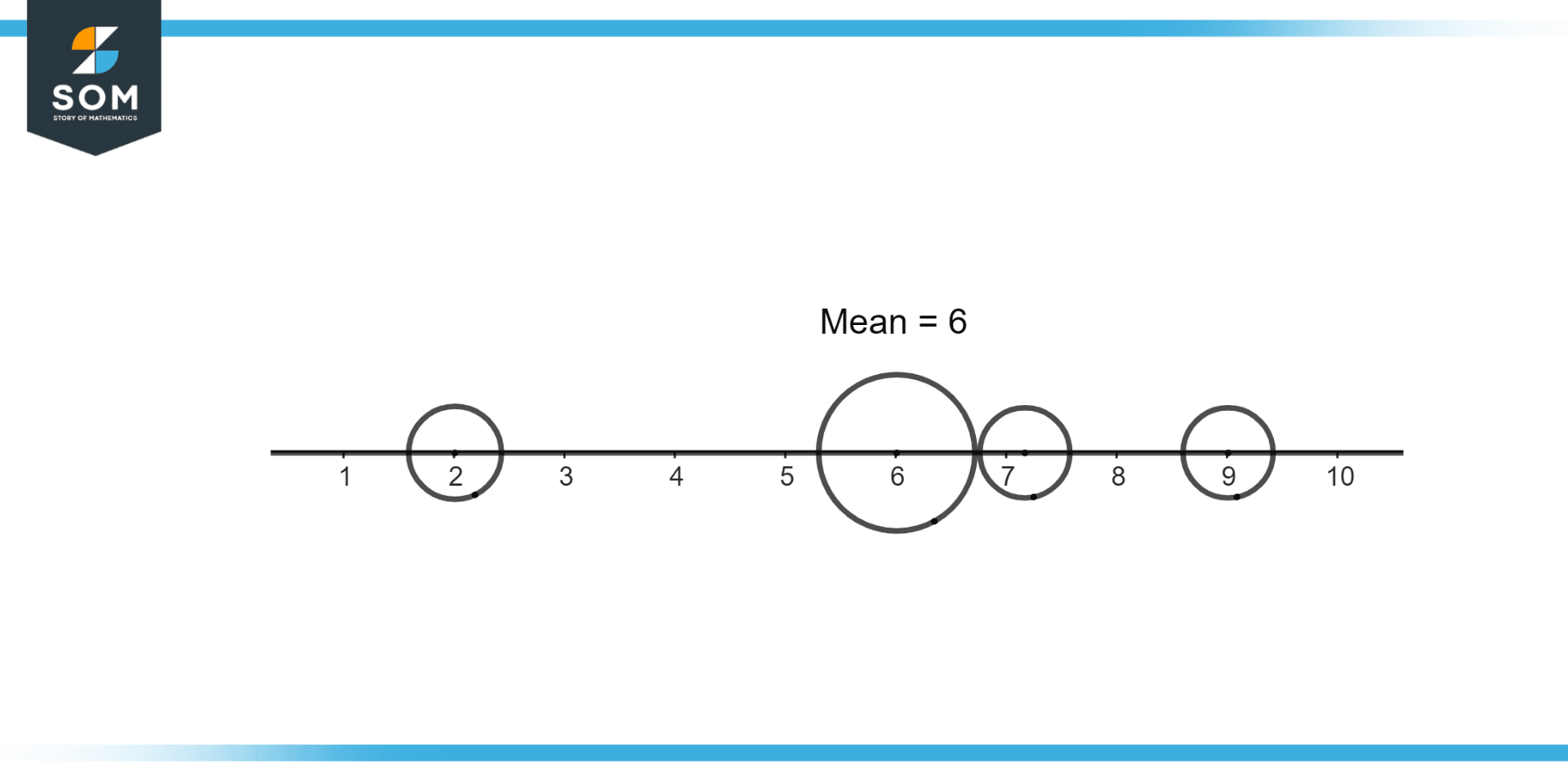
Figure 1 – Average of three numbers 

Figure 1 illustrates the average of three numbers 2, 7, and 9. First, the numbers are added and then divided by the total number of numbers.

In layman’s terms, an average is a single number that symbolizes a collection of numbers; it is often the sum of the numbers divided by the total number of numbers in the collection (arithmetic mean). The average of the 25 digits 2, 3, 4, 7, and 9 is 5, for instance. The mean may also be referred to as the median or mode, depending on the situation.

For instance, the median (a value between 50% and 100% of personal income) is frequently used to describe the typical personal income. The word “average” should be avoided when discussing measurements of central tendency because of this.

The average of the list’s numbers is the same as the number if all of them are the same. The majority of ordinary types have this characteristic. Another universal feature is monotonicity, which states that if two lists of integers A and B have the same length, and each element in list A is at least as large as the corresponding entry in list B, then list A’s average is at least as good as the list’s average. Linear homogeneity is likewise satisfied by all B ways.

If you multiply all the numbers in the list by the same positive number, their average will change by the same factor.

Before calculating the average, certain forms of averages give the list’s items various weights. The weighted median, weighted geometric mean, and weighted arithmetic mean are a few examples. In certain forms of moving averages, an item’s weight is also based on where it is on the list.

However, most kinds of averages satisfy permutation independence. All elements are counted equally in determining the average. Their position in the list does not matter. The mean of (1, 2, 3, 4, 6) is the same as the mean of (3, 2, 6, 4, 1).

The first record that the arithmetic means for using estimates was extended from 2 cases to n cases was in the 16th century. Since the late 16th century, it has become a popular method for reducing measurement errors in various fields. At the time, astronomers wanted to get the true value from noisy measurements such as B. Planetary position or moon diameter.

Scientists

assumed that the average of several measurements would yield a number with a relatively small error compared to the sum of all measurements. In fact, methods of averaging to reduce observation errors were primarily developed in astronomy.

It is the intermediate range (the average of the two extreme values) that is considered a precursor to the arithmetic mean and is used, for example, in Arabic astronomy from the 9th century to the 11th century, but also in metallurgy and navigation.

Median

The center value, if the groups were lined together, would be the median. (If the sum is even, use the average of the middle two.) The greatest and lowest value pairings should be continually removed until only one or two values are left in order to get the median. Sort the list according to the size of its items to do this.

If exactly one value remains, it is the median. If there are two values, the median is the arithmetic mean of these two. This method takes lists 1, 7, 3, 13 and tells it to read 1, 3, 7, 13. Then 1 and 13 are removed to get Listings 3 and 7. This remaining list has two items, so their arithmetic mean (3 + 7)/2 is 5, which is the median.

Mode

In a list, the most frequently occurring number is the mode. For instance, the list’s mode is 3 for (1, 2, 2, 3, 3, 4). Two or more numbers may appear the same number of times, more often than any other number. There is no agreed mode definition in this case. Some authors say they are all modes, while others say there are no modes.

Steps to Calculate Average

You can easily calculate the average of a given set of values. Just sum all the values and divide the result by the number of values given. Averages can be calculated in three easy steps. They are:

Step 1: Sum the Numbers

Finding the total of all provided numbers is the first step in calculating the average of a set of numbers.

 Step 2: Observations

 Then count the number of digits in the given dataset.

Step 3: Average Calculation

The total is divided by the quantity of observations as the last step in determining the average.

Arithmetic Mean

Arithmetic mean is the most common type of average. Given n numbers, each number is denoted by $a_i$ (where i = 1,2, …, n), and the arithmetic mean is the sum divided by n.

Geometric Mean

By determining the nth root of the product of n numbers, the geometric mean is a technique for determining the central tendency of a set of numbers. This is quite different from the arithmetic mean, which adds observations and then divides the sum by the number of observations. However, the geometric mean finds the product of all observations and the product’s nth root, where n is the total number of observations.

Harmonic Mean

According to its definition, the harmonic mean is the reciprocal of the averaged reciprocals of the provided data values.

Average Of Negative Numbers

The process or formula for finding the average is the same if there are negative numbers in the list.

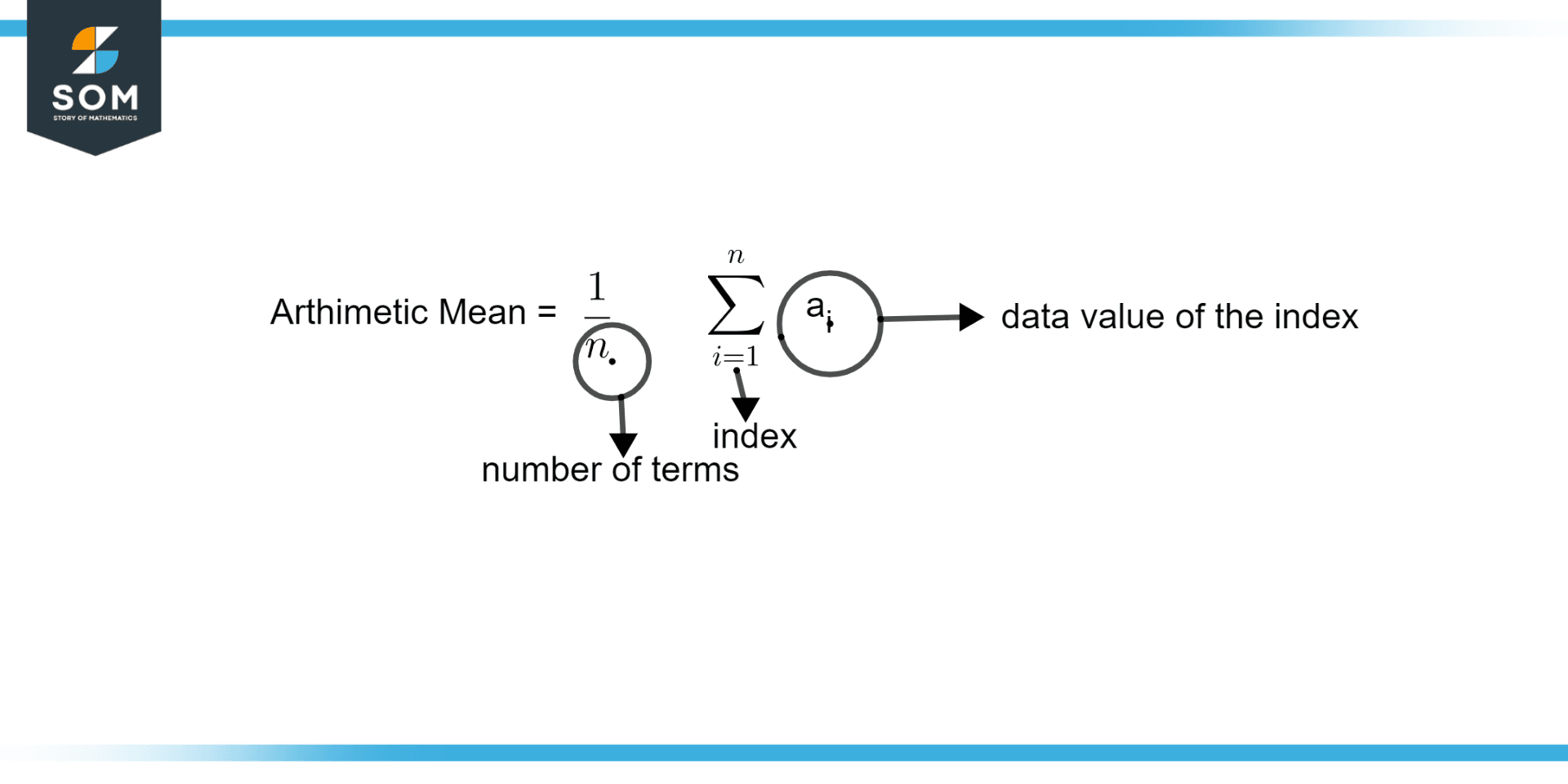
Figure 2 – Formula for Arithmetic Mean

Figure 2 illustrates the formula for the arithmetic mean

Some Examples of Average

Example 1

Find the average of following

a) 3, -7, 12, 6, -2

b) 2, 6, 9, 10

c) 1, 3, 5, 8, 3

Solution

a) In order to evaluate the average, we have to find the sum, which is:

3 – 7 + 12 – 2 + 6 = 12

the total unit is equal to five, so the average will be equal to:

Average = $\dfrac{12}{5}$

Average = 2.4

So the average will be equal to 2.4.

b) In order to evaluate the average, we have to find the sum, which is:

2 + 6 + 9 + 10 = 27

the total unit is equal to four, so the average will be equal to:

Average = $\dfrac{27}{4}$

Average = 6.75

So the average will be equal to 6.75.

c) In order to evaluate the average, we have to find the sum, which is:

1 + 3 + 5 + 8 + 3 = 20

the total unit is equal to five, so the average will be equal to:

Average = $\dfrac{20}{5}$

Average = 4

So the average will be equal to 4.

Example 3

Illustrate the average of 1, 3, 5 on the real line.

Solution

The sum of the numbers 1 + 3 + 5 is equal to 9, and the total units are equal to 3, as illustrated in figure 3.

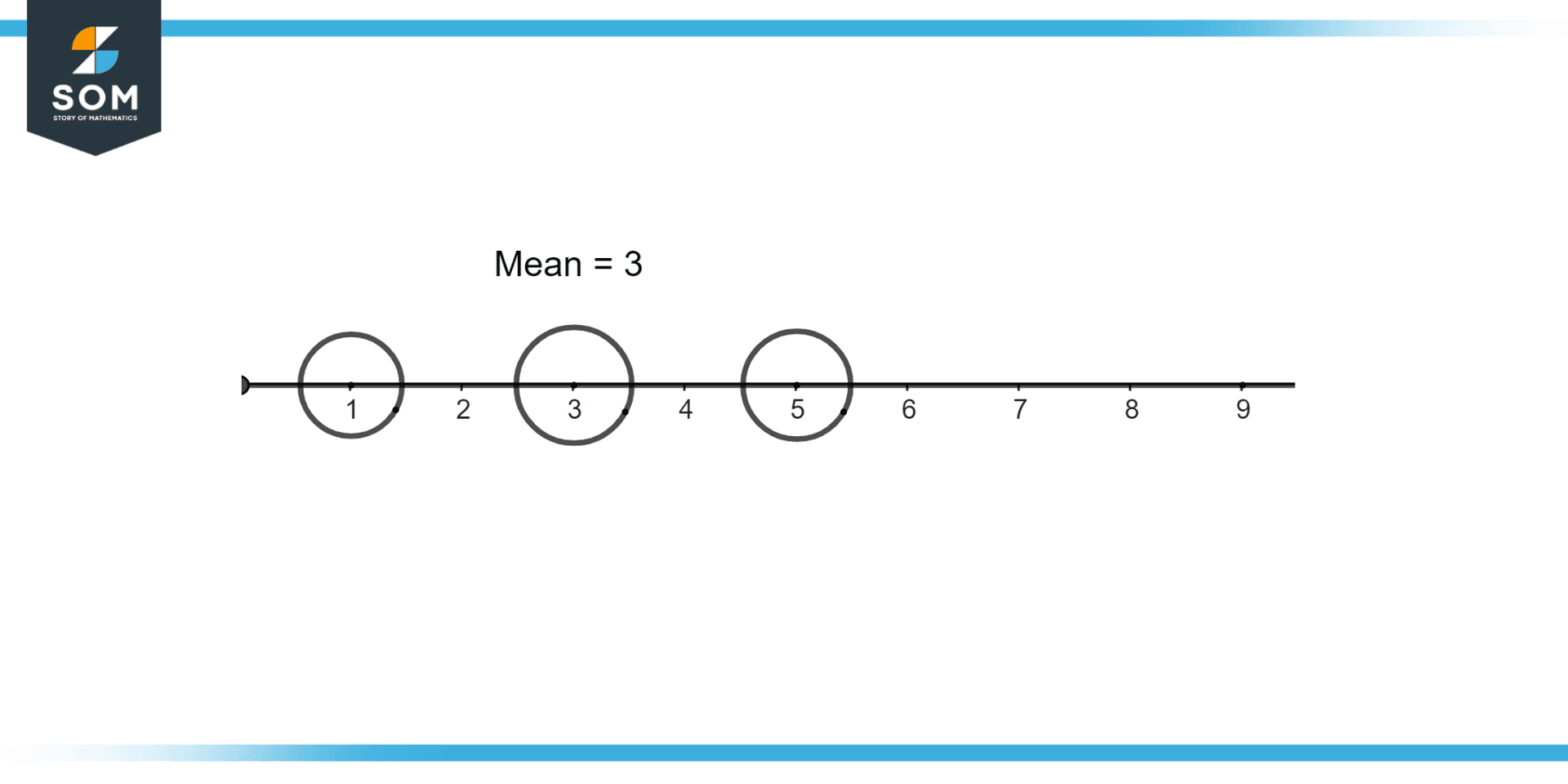
Figure 3 – Mean of Real numbers

All images were created using GeoGebra.

Attribute Definition < Glossary Index > Axes Definition