Axiom|Definition & Meaning

Axiom Synopsis 

An Axiom is a logical statement that is proved to be true through some observation or calculation upon which a mathematical model is formed. They act as laws upon which theories are formed. Sometimes we may not have a direct proof for an axiom but through observation, it might seem self-evident enough for one to even question its logic.

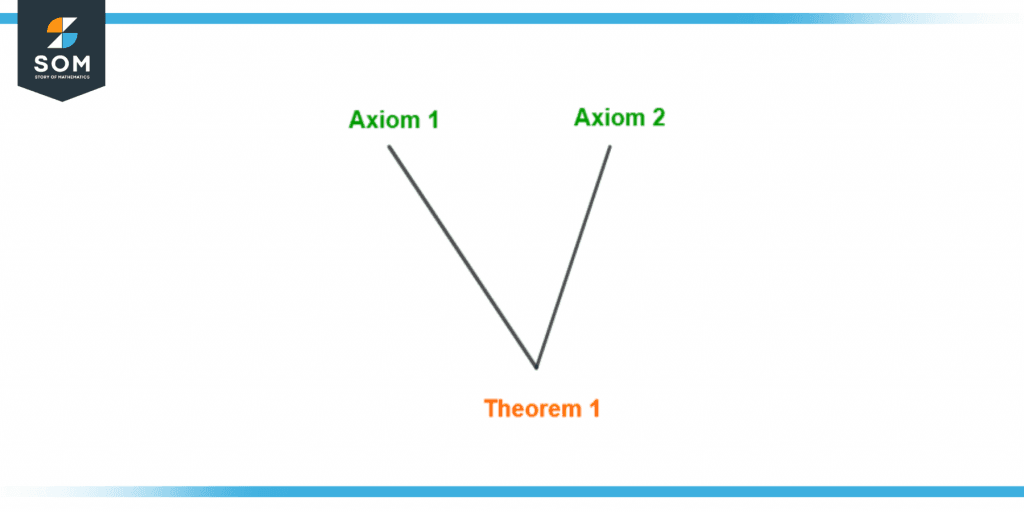
Figure 1 – Relation of Axiom with Theorem

Theoretical Comprehension

Let us take an example you have to find the unknown length of a triangle. To prove this Pythagoras’ theorem will be taken into account. We use proofs to make a logical statement in mathematics because this concept of deriving equations based on logical statements is what makes mathematics and geometry different. 

When we have proved a statement then it becomes a theorem. If a theorem is true or universally correct we call them axioms. Axioms are the helping statements upon which logical statements are formed. 

Axioms play a very important role in this field because if we don’t have enough axioms, it will be difficult to prove anything at all and will result in fewer discoveries whereas if there are too many axioms then anything can be proven easily and the grounds of logic might start crumbling.

Let us look at an example related to this topic for a better understanding of the concepts. As we can see that it is quite possible to draw a straight line from one single point to another point no matter what distance is between these two points. 

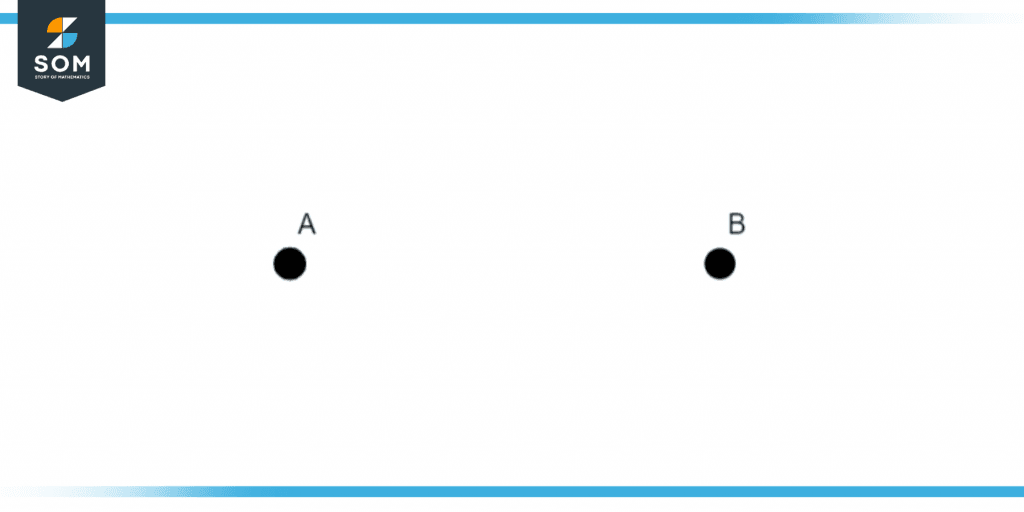
Figure 2 – Two points on a plane

We can see 2 points A and B which are supposed to be at some distance from each other. We can say that it is possible to draw a line starting from point A to point B, and vice versa, without needing to prove it, which is why we consider it an axiom.

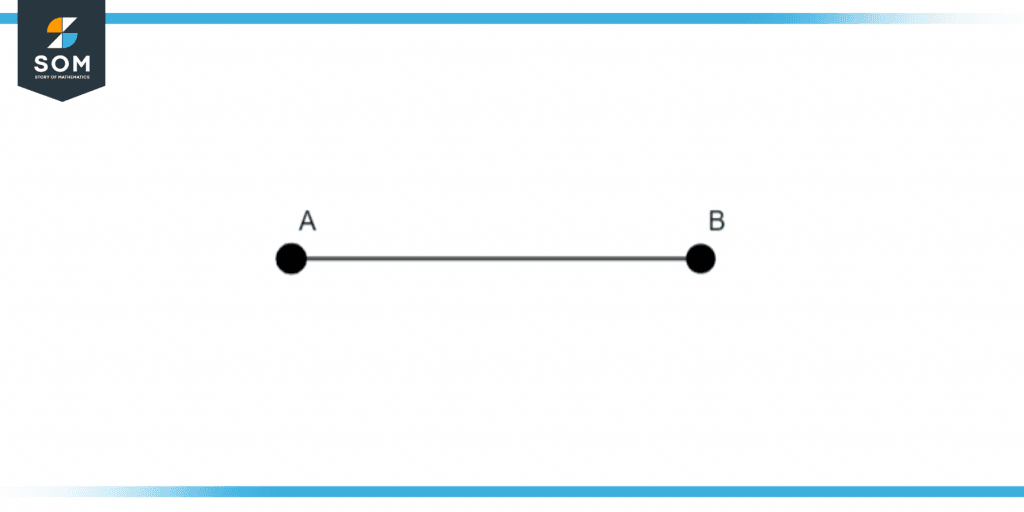
Figure 3 – A line segment

Another type of axiom that we can state is that we can describe any circle by its radius and center. This is true because we can draw any circle with the help of the radius and the center of the circle. 

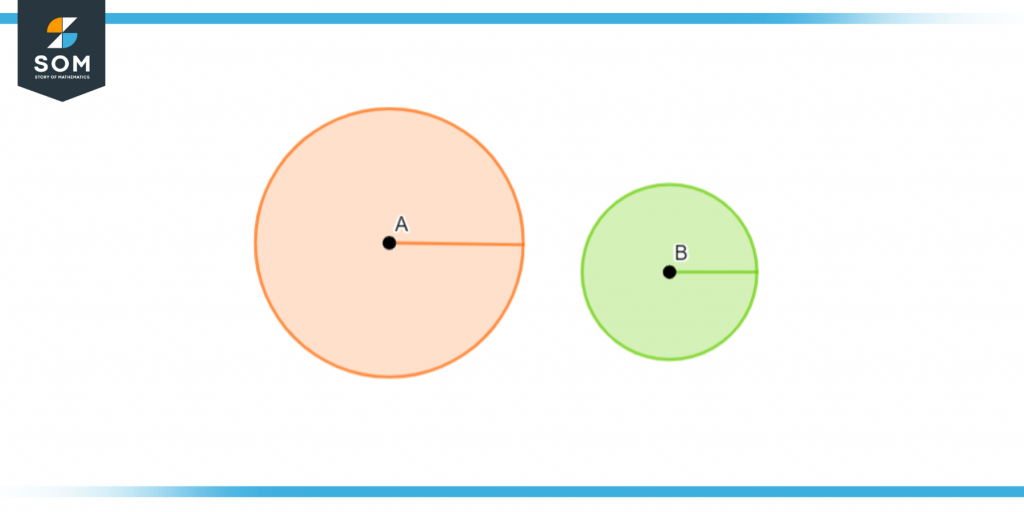
Figure 4 – Two circles with different properties

Now if we take a look at these two circles we can easily say that both have different radii and centers but are defined as a circle upon their specific points.

Note that any theorem may be challenged for its accuracy by other mathematicians whereas axioms are always considered to be true and are not questioned. Similarly, when a theorem’s proof becomes lengthy or has some kind of mistake it can be broken down into small parts using axioms to make it easy for the reader.

Basic Algebraic Axioms

There are many axioms in mathematics but to clear the concepts we are going to take a look at basic axioms which we use constantly. 

The first axiom is the Reflexive Axiom. It is the axiom of equality that states:

A=A

It means that things equal to the same thing will be equal to each other.

 The second axiom is the Symmetric Axiom which states that if;

A=B then B=A

It means that if one thing is equal to another then they will be equal.

The third axiom is the Transitive Axiom which states:

A=B and B=C then A=C

It means that if 2 things are equal to the same thing then they all will be equal to each other.

Then comes the Additive Axiom which states:

If A=B and C=D 

Then A+C = B+D

It means that equal quantities when added together will be equal to each other.

The fifth axiom is the Multiplicative Axiom which states:

If A=B and C=D 

Then AC = BD

It means that equal quantities when multiplied together will be equal to each other because multiplication is just repeated addition.

Pictorial Representation

Axioms are self-evident and don’t need to be proven. This is because axioms can be observed to be true in such a way that logically they will have the high ground without any need for calculations. For example:

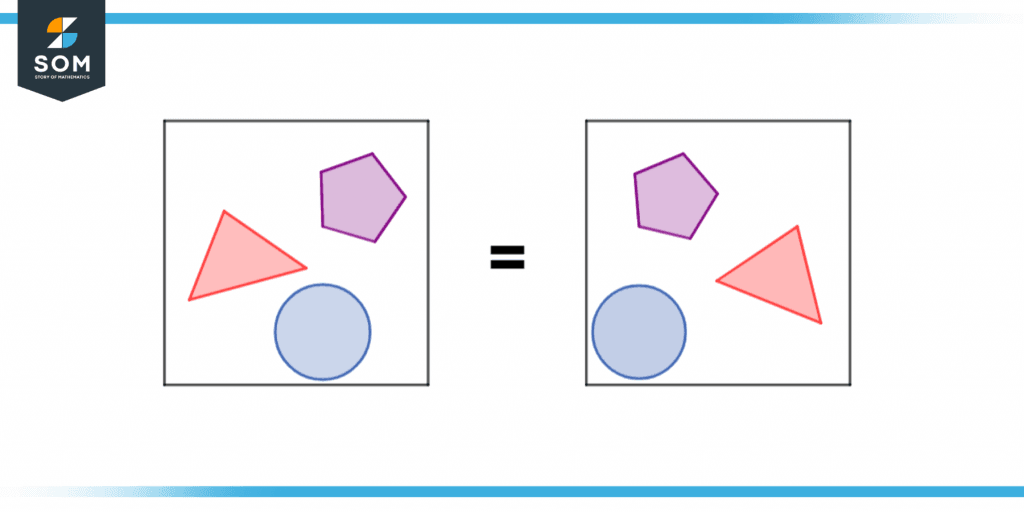
Figure 5 – Two sets with the same elements

The following sets both contain the same elements concerning each other. This shows that the axioms are pretty obvious and do not require any proof. 

There are many types of axioms but to get an understanding we can use this example:

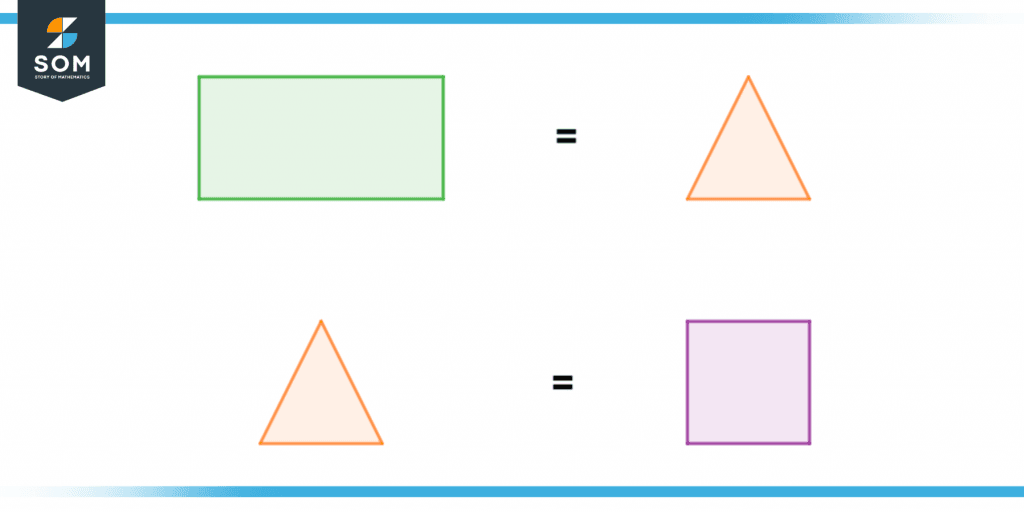
Figure 6 – Transitive Axiom

It shows that if a rectangle is equal to a triangle and that triangle is equal to a square so as we have discussed above the transitive axiom will be implemented which states that when 2 things are equal to 1 thing then all 3 of those things are equal to each other

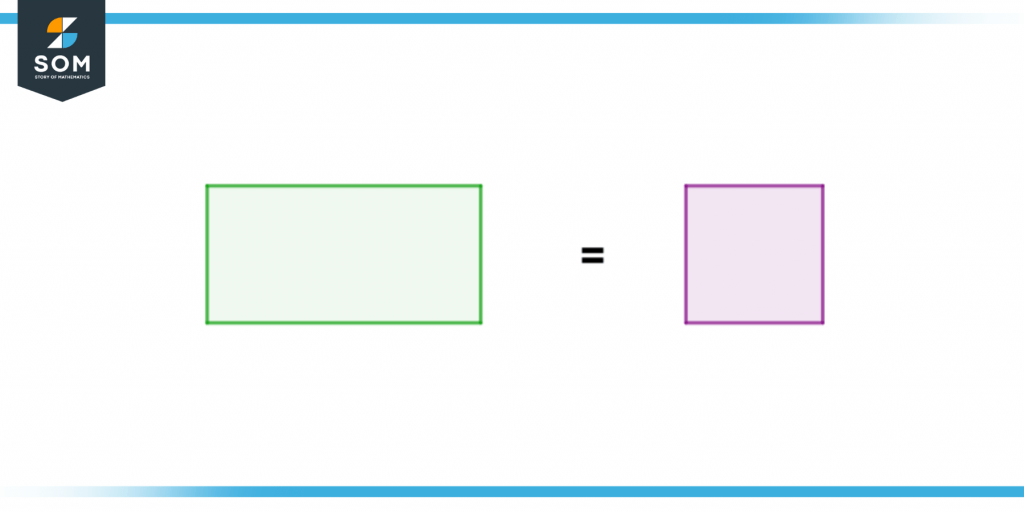
Figure 7 – Equality shows the existence of the axiom

As we can see that since both square and rectangle were equal to the triangle so this means that they are equal to each other

Solved Examples of Axioms

Example 1

Proof 2 lines to be parallel to each other.

Solution

We can prove that 2 lines are parallel to each other by using an axiom that has been given to us. 

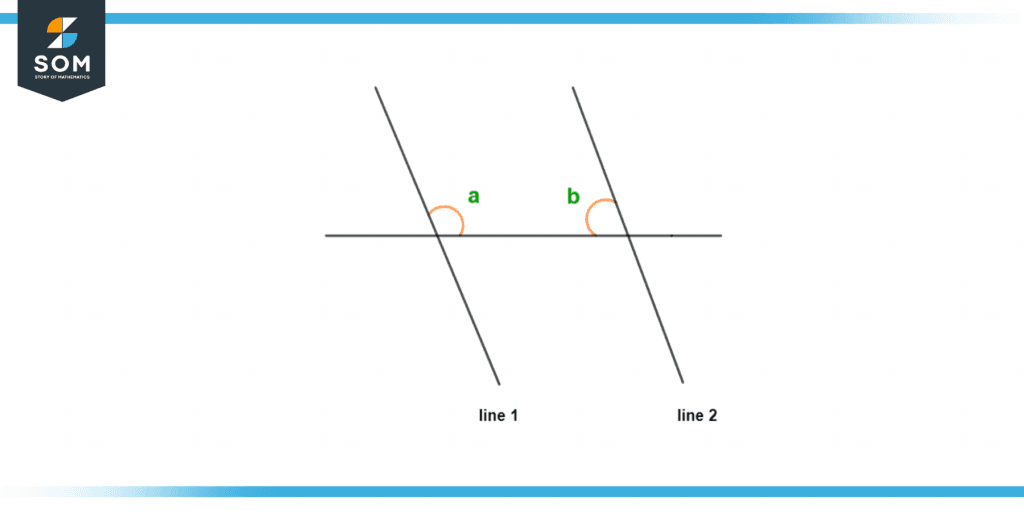
Figure 8 – Two lines intersecting a line at a certain angle

Let us consider these two lines which are intersecting with another line at a certain angle. For line 1 we have angle a and for line 2 we have angle b. As we have an axiom that states:

If a + b = 180°, then both line 1 and line 2 are parallel to each other.

Example 2

State the difference between axiom and theorem

Solution

1. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven.
2. An axiom serves as the base for a theorem to be proved.
3. A theorem may be challenged whereas an axiom is taken as a universal truth.
4. Axioms may be categorized as both logical and non-logical.

Example 3

Proof the following theorem using axioms

AB + A’C = (A + C) (A’ + B)

Solution

We will start by solving the RHS to prove LHS.

RHS = (A + C) (A’ + B) = AA’ + A’C + AB + CB

Now, using AA’ = 0:

AA’ + A’C + AB + CB = 0 + A’C + AB + BC

= A’C + AB + BC(A + A’)

= AB + ABC + A’C + A’BC

Now using ABC + A’BC = 0:

= AB + A’C = LHS

Hence Proved RHS = LHS.

Images/mathematical drawings are created with GeoGebra.

Axes Definition < Glossary Index > Axis Graph Definition