Base (Geometry)|Definition & Meaning

Geometry and Its Importance in Mathematics 

Geometry is one of the most fundamental branches of mathematics. It deals with the spatial properties of shape. With roots at least as far back as the periods of Pythagoras, Euclidean, and other ancient Greek “natural philosophers,” geometry is an original branch of mathematics and is actually the most ancient of all sciences. Geometry was initially studied to comprehend the physical universe in which we exist, and this tradition is still present today.

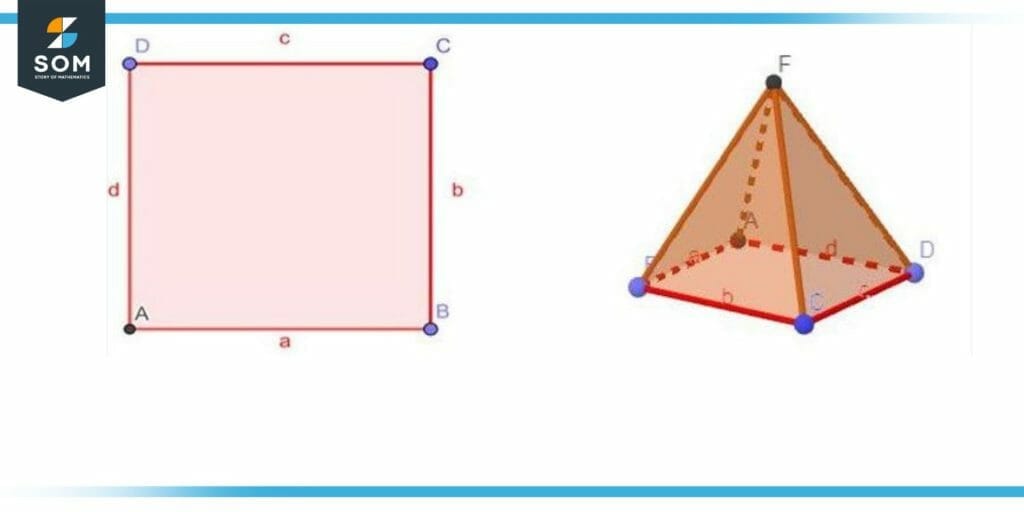
Figure 1 – The two-dimensional base of a three-dimensional shape (a pyramid in this case).

It is one of the oldest fields of mathematics and gets its name from Greek terms that mean “Earth measuring.“It developed in reaction to real-world issues like those in surveying. It was eventually understood that geometry need not be restricted to the study of hard 3-dimensional objects and flat surfaces (plane geometry and solid geometry), but rather that even the most abstract ideas and concepts may be expressed and developed in geometric terms.

There are different types of geometry: Euclidean, non-euclidean, differential, analytical, and projective geometry.  Many geometrical shapes in 3D are created using a regular 2 Dimension shape. The 2D shape which is used is known as the base of that 3 Dimension figure. In 2D figure base is a line segment, whereas, in 3D, the figure base is a 2 Dimension shape.

Figure 1 illustrates a 2-dimensional figure and 3-dimensional figure in which  line segment AB is the base of the square illustrates a  the plane ABCD is the base of the pyramid. Shapes are also categorized according to how uniform or regular they are. A regular form, such as a square, circle, etc., is typically symmetrical. Asymmetrical forms are irregular shapes.

They are also known as organic forms or free form shapes. For instance, a tree’s form is erratic or organic. The 2-dimensional forms in plane geometry are flat and closed shapes like circles, squares, rectangles, and rhombuses, among others. The 3-dimensional forms in solid geometry are the cube, cuboid, cone, sphere, and cylinder. All of these forms are visible to us in daily life. Figure 3 and figure 4 illustrate the example of 2-dimensional and 3-dimensional shapes respectively.

In geometry, the base is the side of a polygon or the face of a polyhedron, specifically the one oriented perpendicular to the direction in which the height is measured, or what is considered the “floor” in the figure. Bases are defined as the bottom of the figure but they are not limited to being the bottom of the figure.

Bases are often termed as the elevation perpendicular to the base in both 2-D and 3-D. Bases are used to calculate the area, volume, and perimeter of different shapes. Different formulas involving the base of shapes are given below.

Area of Triangle = $\dfrac{1}{2}$ x base x height

Area of Rectangle =2 x (base + height)

Area of Rectangle = base x height

There may be one or several bases on a solid object. Most geometric shapes such as a prism, for instance, have two bases. The top of one base is at the bottom of the other. They run parallel to one another. As one of the essential ideas in geometry, the concept of the base is crucial to understand. This will make it simpler for higher courses to understand difficult geometrical ideas. However, some geometric shapes are also created utilizing other shapes.

A pyramid would have one rectangle and four triangles. The rectangle is referred to as the shape’s base in that situation. A circle or an ellipse serves as the basis of a cylinder. Figure 4 illustrates the concept of geometric shapes with more than one base.

Representation of Bases of Different 2-D Shapes

In figure 2 the black line segment illustrates the base of the shapes.

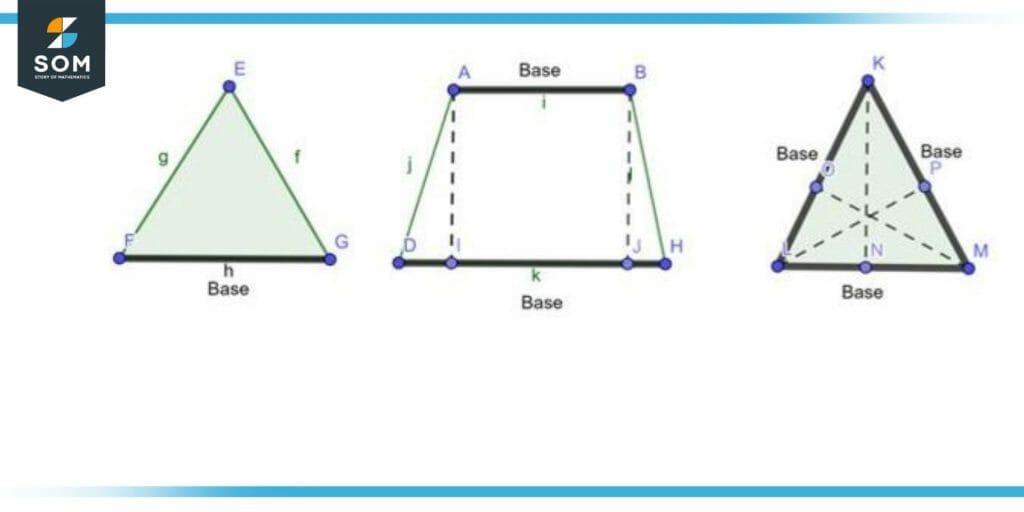
Figure 2 – Base of two Dimensional shape

Representation of Bases of Different Bases of 3D Shapes

In figure 3 the black area illustrates the base of the shapes.

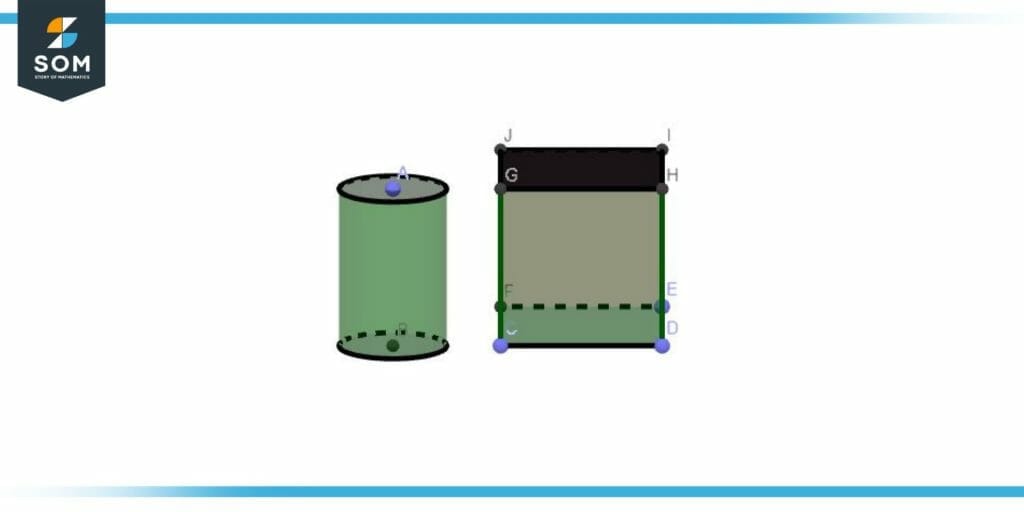
Figure 3 – Bases for Three dimension shapes

Extended Bases and Their Importance

Extended bases are used in special cases such as obtuse triangles. In an obtuse triangle, the extended base has termed the extension of the edge. In the case of acute angles, the elevation from the apex of the acute angle lies outside the triangle and intersects the extended opposite base perpendicularly. Figure 4 illustrates the concept of extended bases.

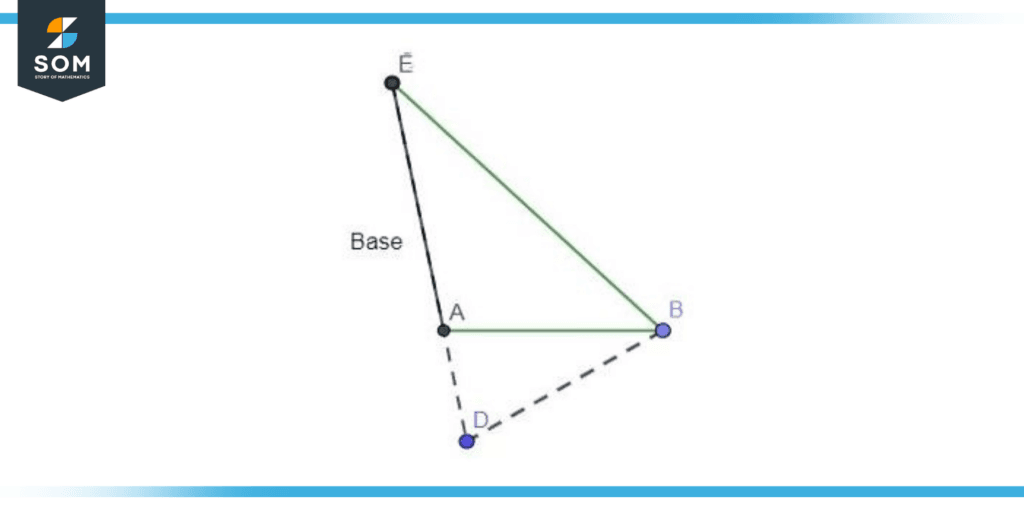
Figure 4 – Extended base of an obtuse triangle

Solved Examples Involving Bases of Geometrical Shapes

Example 1

What is the length of the base of the triangle if the area of the triangle is 6 cm sq and the height of the triangle is 4 cm.

Solution

Area of Triangle = $\dfrac{1}{2}$ x base x height

 6  =  $\dfrac{1}{2}$x 4 x base

  Base = $\dfrac{12}{4}$

  Base = 3 cm 

Example 2

Find the base of the obtuse-angled triangle with an area of 14 cm sq and height of 7 cm.

Solution

Area of Triangle = $\dfrac{1}{2}$ x base x height

  14  =  $\dfrac{1}{2}$x 7 x base

  Base = $\dfrac{14×2}{7}$

 Base = 4 cm 

Example 3

Find the base (a) of a given trapezium when the area is 15 m sq .

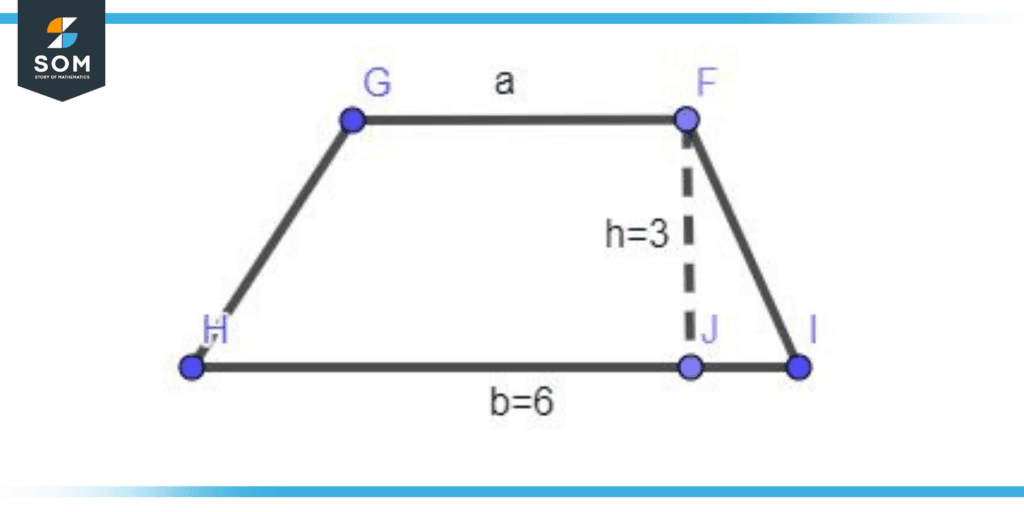
Figure 5 – Trapezium

Solution

Area of Trapezium = $\dfrac{1}{2}$ x (a+b) x height

 14  =  $\dfrac{1}{2}$x (a+6) x height

 a+6 = $\dfrac{15×2}{3}$

 Base = 4 m 

Example 4

What is the length of the base of the square if the perimeter of the square is 16 cm?

Solution

Perimeter of Square = 4 x base

 16  =   4 x base

 Base = 16/4

 Base = 4 cm

All images/mathematical drawings were created with GeoGebra.

Balance Scales Definition < Glossary Index > Base Numbers Definition