JUMP TO TOPIC
Base Numbers|Definition & Meaning
Definition 1
The base number is defined as the number multiplied by itself multiple times and can be written with an exponent. Different numbers multiplying cannot have a base number as it is only a single number and requires self-multiplication.
Definition 2
A base number is also defined as the number of specific or unique digits that are present in a numeral system. The digits are placed in a positional manner that defines the particular value of the digit in the numeral system.
Figure 1 shows the base number 6 multiplied 3 times to get 216.
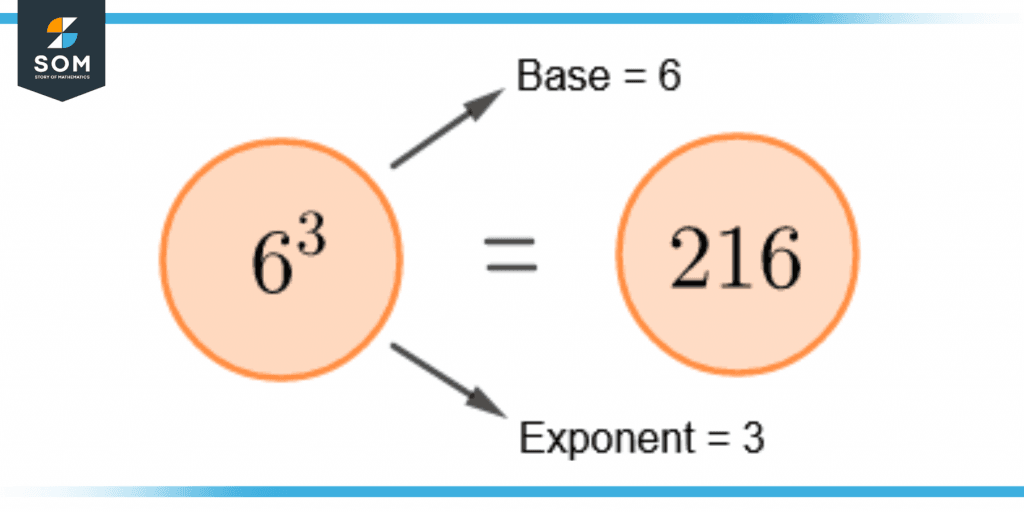
Figure 1 – Demonstration of a Base Number in Multiplication
Base Number in Multiplication
The base number or base in the multiplication operation is the number multiplied in such a way that it can be written with an exponent. The exponent plays a key role while defining the base number.
An exponent is a number that defines the number of times a number is multiplied by itself. It is also known as the power or index of the base number.
Without a base number, there is no meaning of exponent. The exponent is written in superscript to the base number which is multiplied several times.
For example, in $3^2$, 3 is the base number. The number 2 indicates that the base number is multiplied twice, hence the exponent is 2. Also, $3^2$ can also be written with the multiplication operator as 3 × 3.
Consider a multiplication of 4 × 4 × 4 × 4 × 4. As 4 is multiplied five times by itself, so 4 is the base number and 5 is the exponent. This multiplication can also be written as $4^5$. This is demonstrated in figure 2.
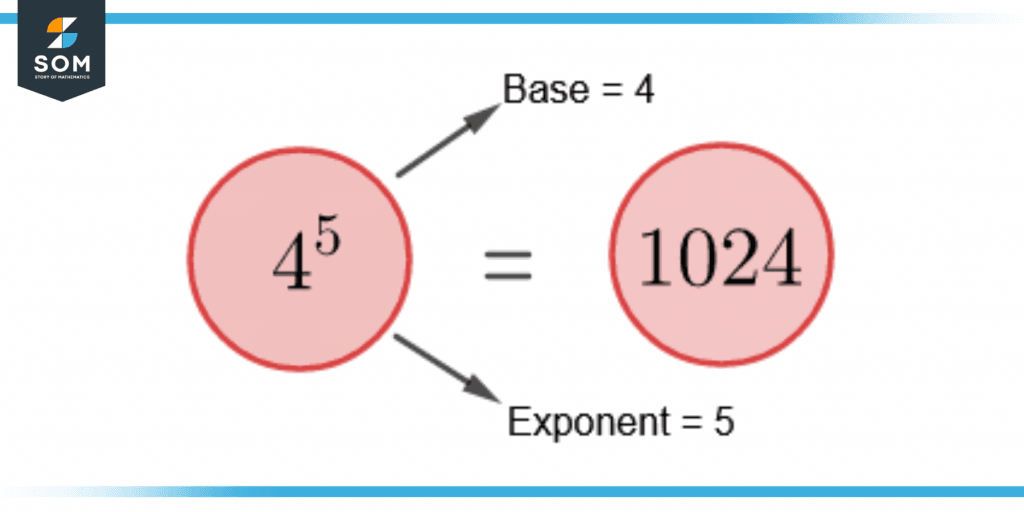
Figure 2 – Demonstration of Base and Exponent
Base Number in Numeral Systems
A base number of a number system defines the number of values unique to a particular numeral system. The set of values has different numerical meanings for different number systems.
The base of a number system is also known as the radix. The base number is written in subscripts to the specific number of a numeral system.
The following four numeral systems have different base numbers according to the number of specific digits or symbols present in that system.
Decimal Number System
The Latin word “Decimus” gives the origin to the word decimal meaning “tenth”.
The decimal number system has the base or radix 10 as it constitutes ten different digits. The unique digits in the decimal number system are from 0 to 9.
All are single-digit numbers and each number has a specific weight and position. This is the most used system in our daily lives.
The conversion of $23_{10}$ from decimal to binary is shown in figure 3.
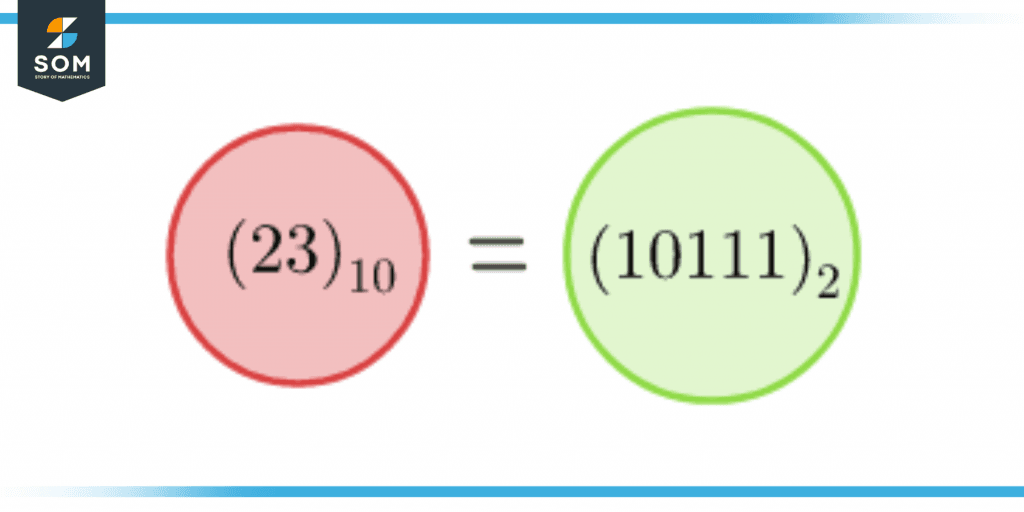
Figure 3 – Conversion from Decimal to Binary Number
Binary Digit System
“Bi” means two. As the name suggests, the binary system consists of two digits 0 and 1, and has the base number 2. The binary system is primarily used in digital logic design such as logic gates.
Binary coding is also used in computers to understand instructions from the user and perform relevant tasks.
For example, ${11110}_2$ is converted to a decimal number shown in figure 4.
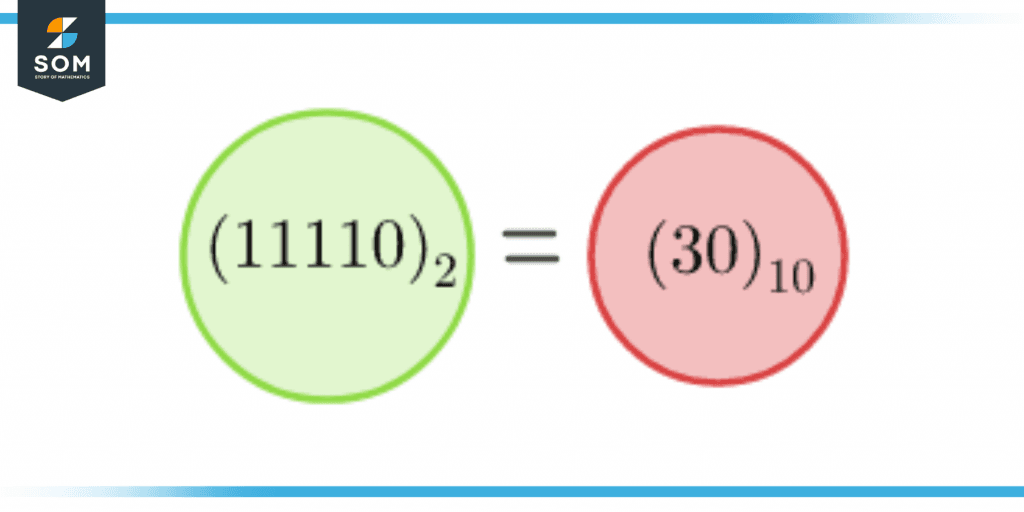
Figure 4 – Conversion from Binary to Decimal Number
Octal Number System
Octal means “eight”. The octal number system has unique digits from 0 to 7 hence it is a base-8 numeral system.
It has fewer digits and is not as common as the decimal number system. Also, it is easy to convert from binary to octal as a octal digit requires only three binary numbers.
For example, ${16}_8$ is converted to a binary number as shown in figure 5.
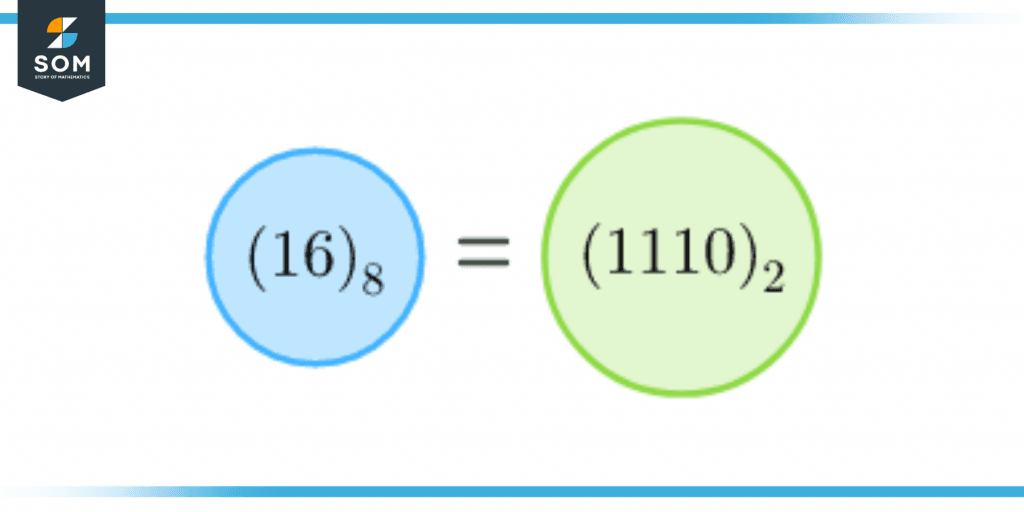
Figure 5 – Conversion from Octal to Binary Number
Hexadecimal Digit System
Hexa means “six”. The hexadecimal number system has the base 16 as it has sixteen different numbers and symbols from 0 to 15.
The two-digit numbers 10, 11, 12, 13, 14, and 15 should be represented by unique symbols to differentiate them from the other numerals. So, they are designated as A, B, C, D, E, and F.
For example, $(41)_{16}$ is converted into decimal as shown in figure 6.
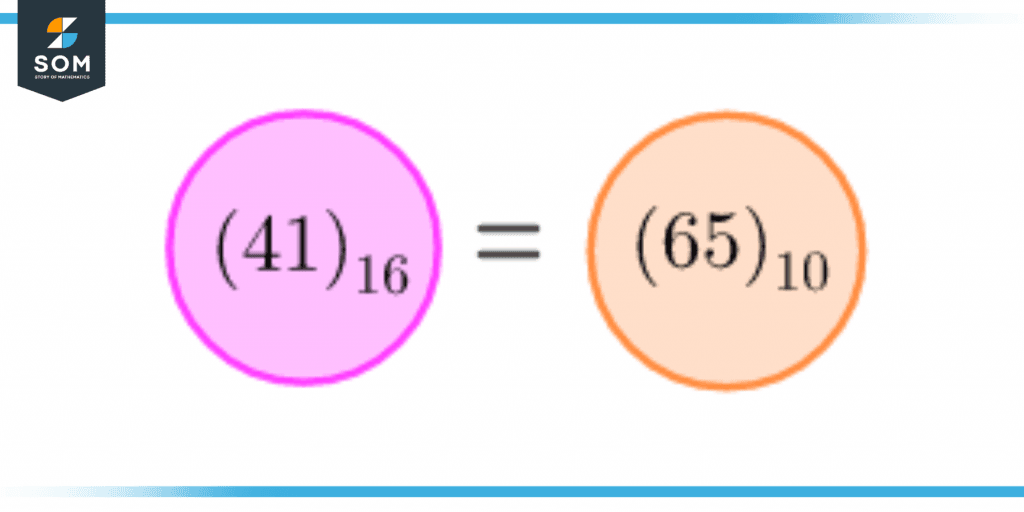
Figure 6 – Conversion from Hexadecimal to Decimal Number
Calculating a Base Number
The base number of a certain number can be identified given the equivalent number in some other numeral system.
For example, 35 is a number whose base number is unknown. But it is given that 35 is equal to $(23)_{10}$. So, how to calculate the base number of 35? Let the unknown base of 35 be b.
First, we need to subtract the one’s place of the base b number which is 5 number from 23 which is given. So 23 – 5 = 18.
Then, we need to divide 18 by the tens place of the base b number which is 3. So, 18 ÷ 3 = 6. So, the base of the number 35 is 6.
The result can be checked by multiplying the tens place of the number that is 3 by 6 and then adding the result with 5. So, {3(6)} + 5 = 23. Hence, $(23)_{10}$ = $(35)_{6}$.
Solved Examples Demonstrating Base Numbers
Example 1
What is the base number in 7 × 7 × 7 × 7 × 7 × 7? Also, write the multiplication in exponent form, find the index and simplify.
Solution
As 7 is multiplied by itself six times, it can be written as $7^{6}$. Here, 7 is the base number and 6 is the exponent or index. The simplification of this multiplication results in 117,649.
Example 2
Convert $(58)_{10}$ into a binary number.
Solution
To convert 58 to a binary number, it is divided by 2 repeatedly and the remainder is written beside the quotient.
When the final quotient is 1 or 0, the binary number is the last quotient and the remainders. This process is shown in figure 7.

Figure 7 – Procedure to Convert Decimal to Binary Number
So the binary number for $(58)_{10}$ is $(111010)_{2}$.
All the images are created using GeoGebra.
