JUMP TO TOPIC
Bearing|Definition & Meaning
Definition
Bearings can be defined as the angles used to measure direction, with the north being taken as a point of reference.
What Are Bearings?
Bearings are a source to express the angle between two things. Bearings must be computed and expressed according to a set of criteria.
- Measurements must always be taken from the North point. Thus, the north direction should be known before measuring bearings.
- Always use three-figure bearings in your responses (thus, 60 degrees would be expressed as 060 degrees).
- Ensure measuring bearings in a clockwise direction.
What Are Compass Bearings and True Bearings?
Compass bearings employ the four positions on a compass in order to determine the position of one object relative to another. These four positions are divided into sixteen different positions across the compass, which are spaced 22.5° apart from one another. For example, the north-northeast (NNE) direction can be reached by starting at the north arrow and moving 22.5 degrees clockwise. 22.5 more degrees later, we arrive in the northeast (NE). This keeps happening as we circle the compass until we get back to the starting point.
The name of the direction invariably begins with north or south, as in northeast or southwest, when it is at a 45° angle between two pure directions.
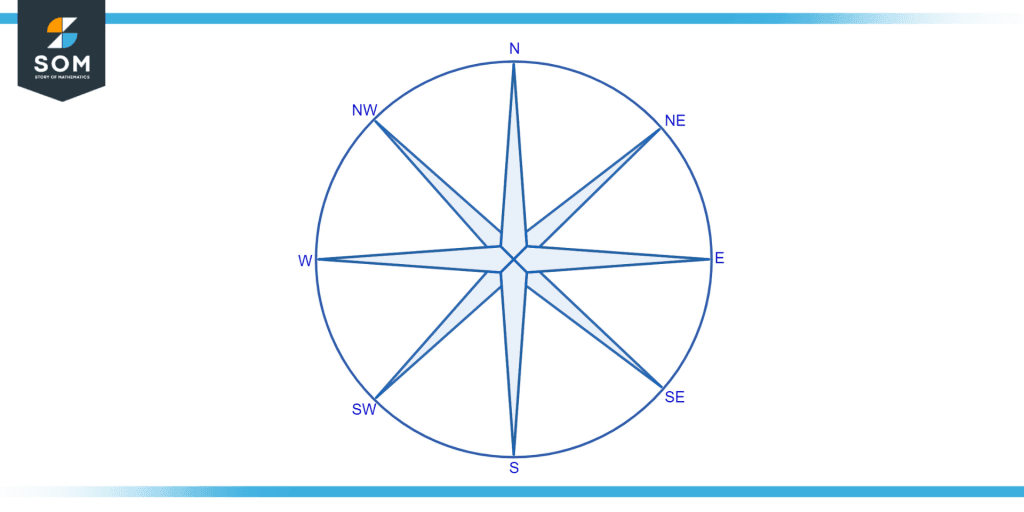
Figure 1: Illustration of a Compass Bearing
True bearings take into account the number of degrees an object measure clockwise from the north—for example, 120°. To locate an item, True Bearing is extremely useful in air traffic control and surveying. Let us say we wish to measure the true bearing of an object at point A from another point B. In order to determine the true bearing, we place point B on the compass’ center. After that, we move clockwise, starting from the north point till we reach line AB. The true bearing of point B from point A is at this angle.
Measuring Bearings
Let us now discuss how can we determine bearings between two points using a protractor in a stepwise manner.
- Determine the location from where you are taking the bearing and plot the north line if one has not already been plotted.
- With the use of the protractor, put the scale’s zero on the north line. Calculate the necessary angle clockwise, and then write a note on your page at the required angle.
- Mark a line from the starting spot that points in the bearing’s direction. Use this scale properly if you are creating a scale drawing and are aware of the distance needed to find a point.
Now let’s employ the above-mentioned method to measure the bearing of the point in the below diagrams:
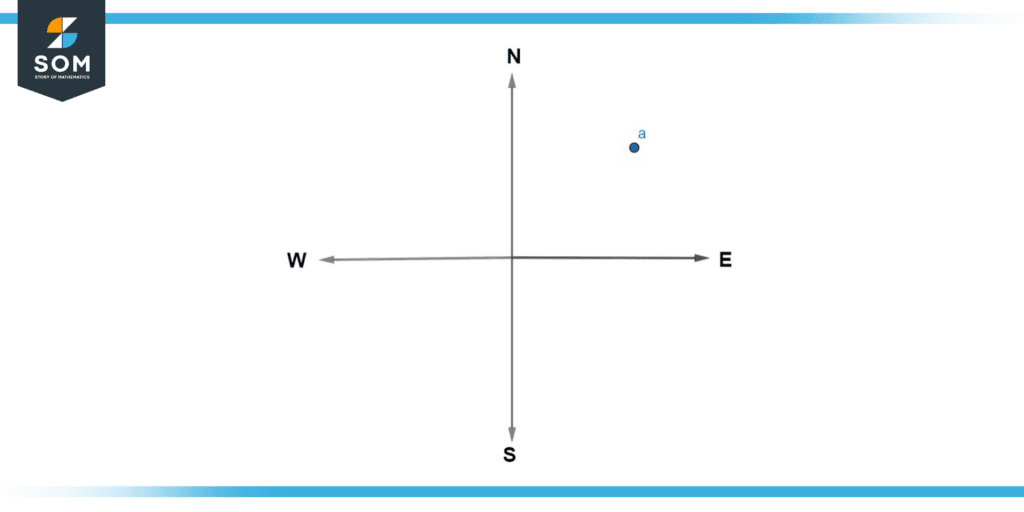
Figure 2: Illustration of Example (a)
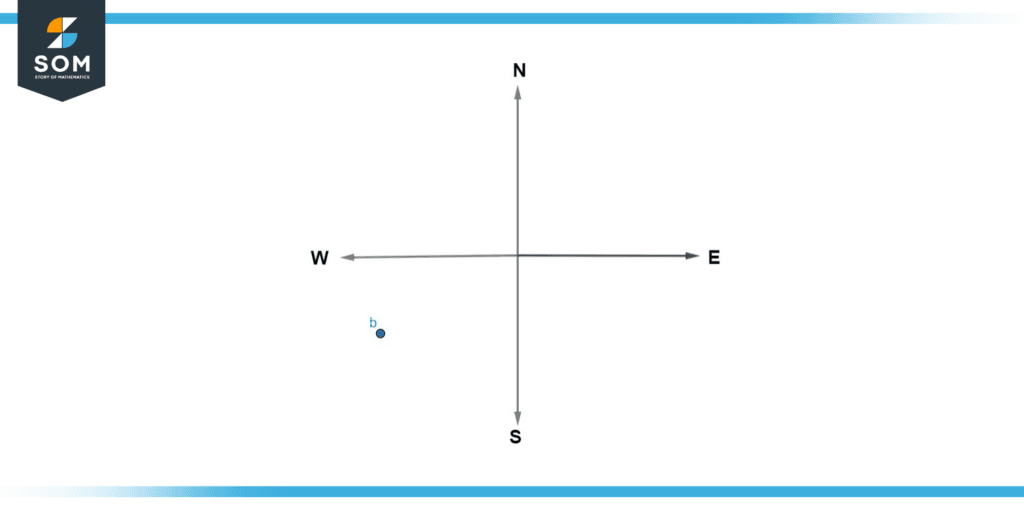
Figure 3: Illustration of Example (b)
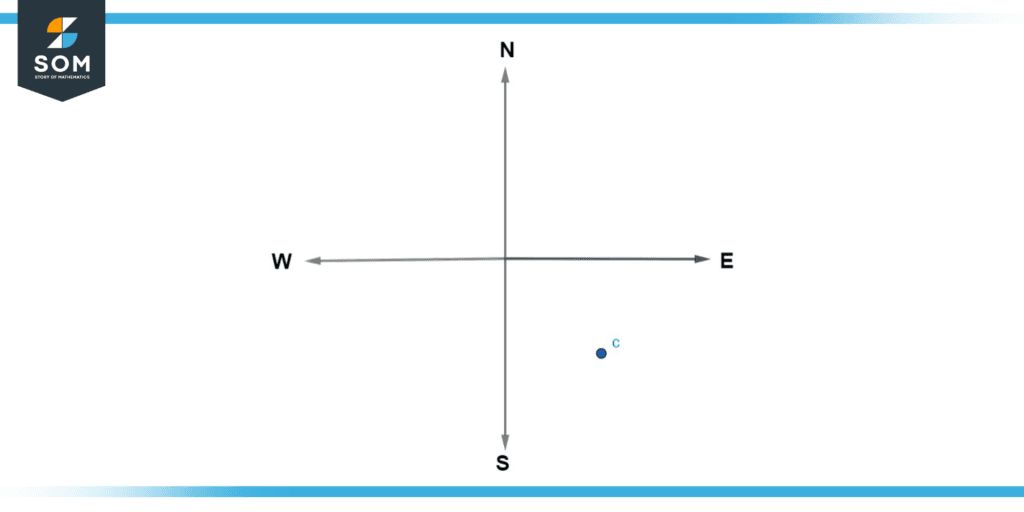
Figure 4: Illustration of Example (c)
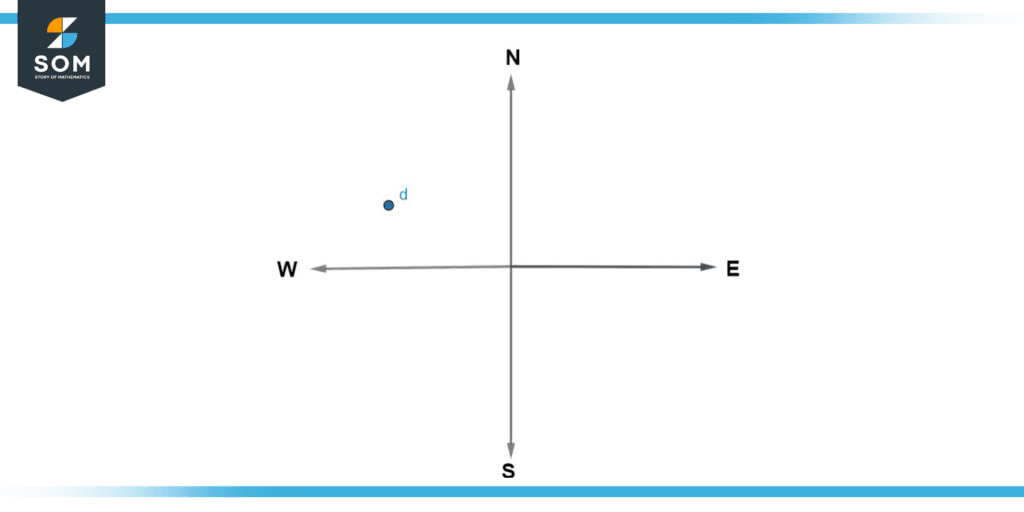
Figure 5: Illustration of Example (d)
Point “a”
Draw a line joining Point “a” and the centre of the compass. Place the protractor at the centre of the compass and plot the angle in the clockwise direction between the north line and the line of point “a”.
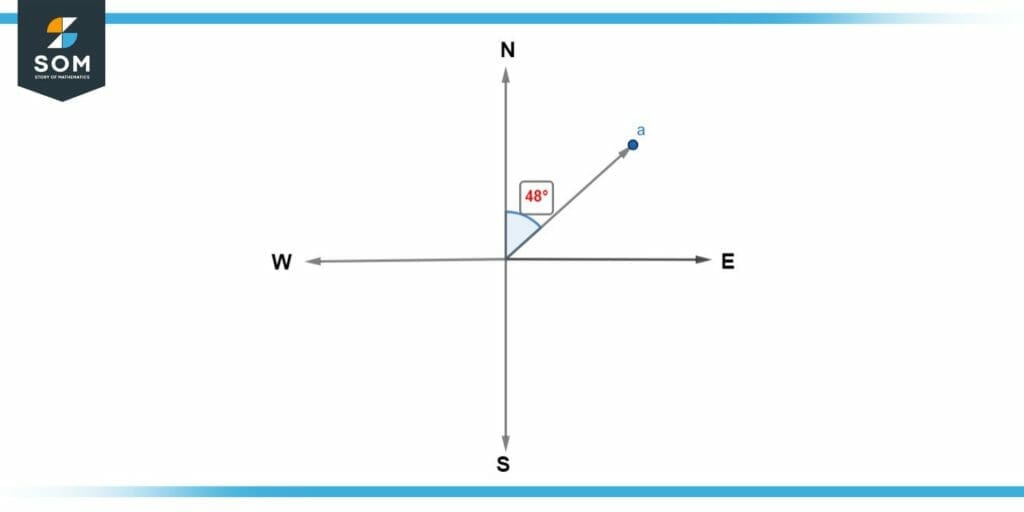
Figure 6: Solution of Example (a)
Thus, in this manner, we found that the bearing of “a” is 48°.
Point “b”
Begin by joining point “b” with the centre of the compass. Just like in the previous example, place the protractor at the centre of the compass and plot the angle in a clockwise direction between line “b” and the south line as shown in the picture below.
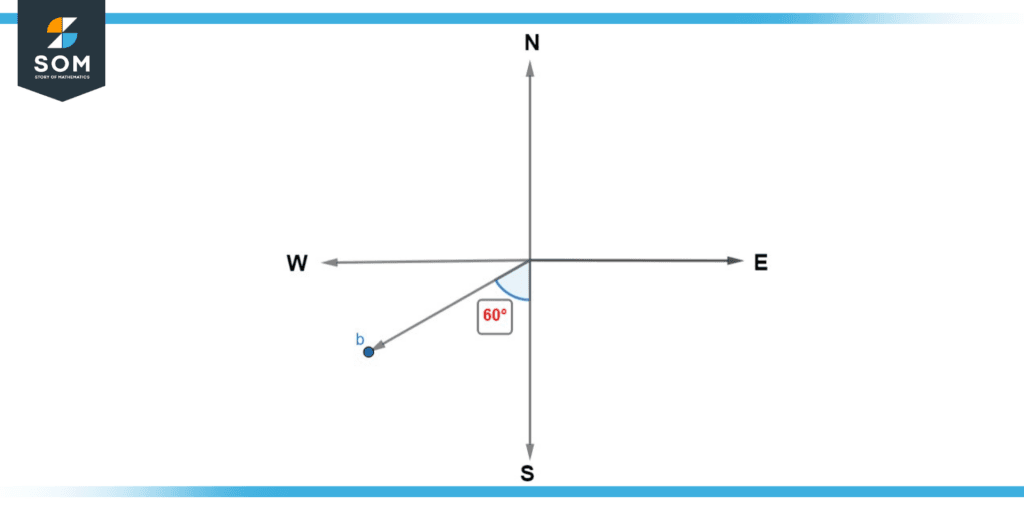
Figure 7: Solution of Example (b)
As we know that point S refers to 180°. We can also see in the above diagram that the desired angle is 60° greater than 180°. Thus, the angle we plotted between the north line and the line that is joining point “b” with the centre of the compass can be calculated as 60o + 180 o = 240o.
Hence, we found that the bearing of point “b” is 240°.
Point “c”
Just like the above examples, draw a line joining Point “c” with the centre of the compass. Place the protractor at the centre of the compass and plot the angle in the clockwise direction between the east line and the line of point c”.
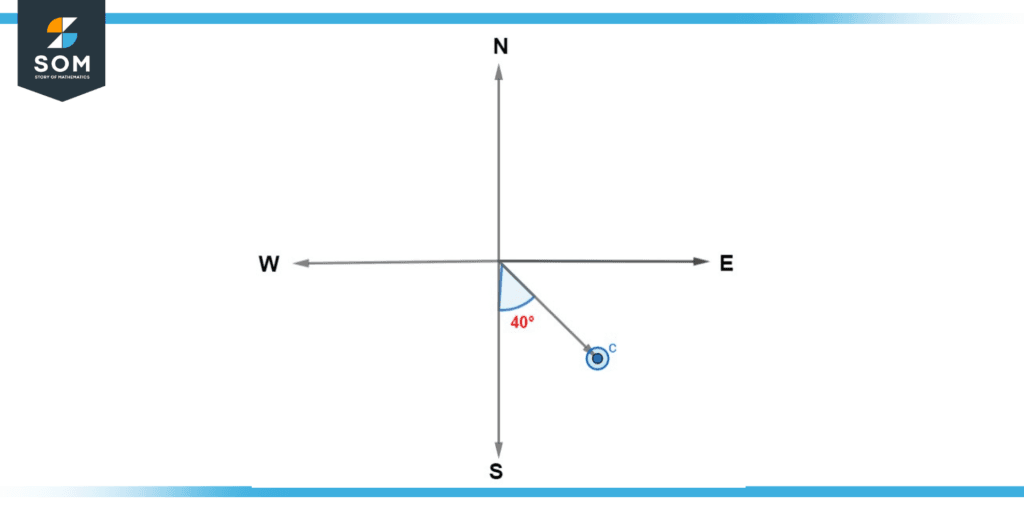
Figure 8: Solution of Example (c)
As mentioned above, point S refers to 180°. Furthermore, it can clearly be seen in the above diagram that the desired angle is 40° smaller than 180°. Hence, the angle we plotted in a clockwise direction between the north line and the line that is joining point “b” with the centre of the compass can be calculated as 180o – 40o = 140o.
Thus, in this manner, we found that the bearing of point “c” is 140°.
Point “d”
Similarly, in this example too, draw a line joining Point “d” with the centre of the compass. Place the protractor at the centre of the compass and plot the angle in the clockwise direction between the west line and the line of point “d”.
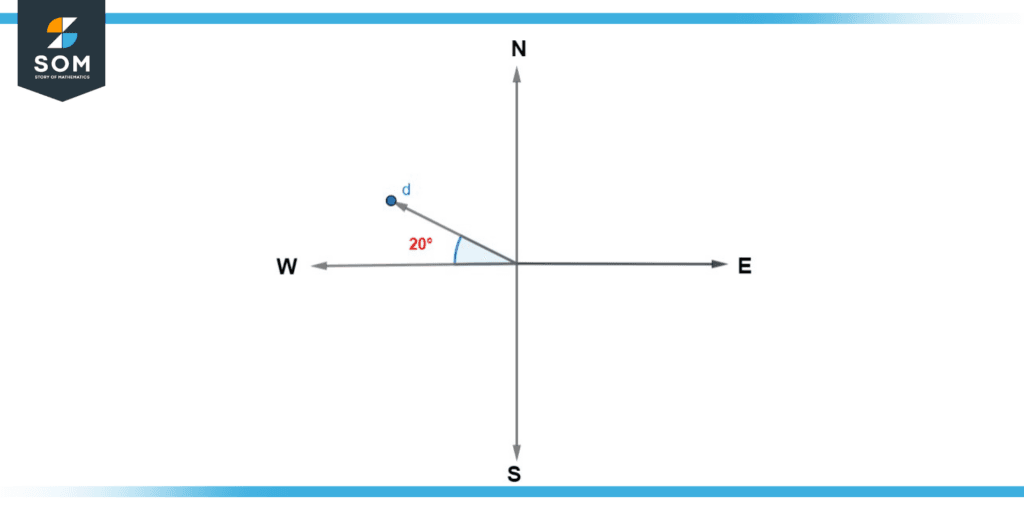
Figure 9: Solution of Example (d)
Now we know that point “W” in the above diagram refers to 270°. Also, we can clearly see in the above diagram that the desired angle is 20° greater than 270°. Therefore, the angle we plotted in a clockwise direction between the north line and the line that is joining point “b” with the centre of the compass can be calculated as 270o + 20o = 290o.
Hence, in this manner, we found that the bearing of point “d” is 290°.
A Few Examples of Finding Bearings
Example 1
What is the true bearing of a person travelling in the following compass bearings?
- South?
- North-East?
- West?
- North-North-East
Solution
- The true bearing of the South line on the compass is 180o.
- The true bearing of the North-East direction on the compass is 045o.
- The true bearing of the West line on the compass is 270o.
- The true bearing of the North-North-East direction on the compass is 5o.
Example 2
Find out the compass bearing of the true bearings given below.
- 135°
- 315°
- 225°
- 5°
Solution
- The compass bearing of the true bearing 135° is South-East.
- The compass bearing of the true bearing 315° is North-West.
- The compass bearing of the true bearing 225° is South-West.
- The compass bearing of the true bearing 157.5° is South-South-East o.
Images/mathematical drawings are created with GeoGebra.
