JUMP TO TOPIC
Benchmark Angles|Definition & Meaning
Definition
Benchmark angles are such angles that are used as a reference or standard to estimate other angles such as acute and obtuse angles closer to them. These angles have exact values of trigonometric ratios which makes the calculations easier with chances of fewer errors.
Figure 1 shows a demonstration of benchmark angles.
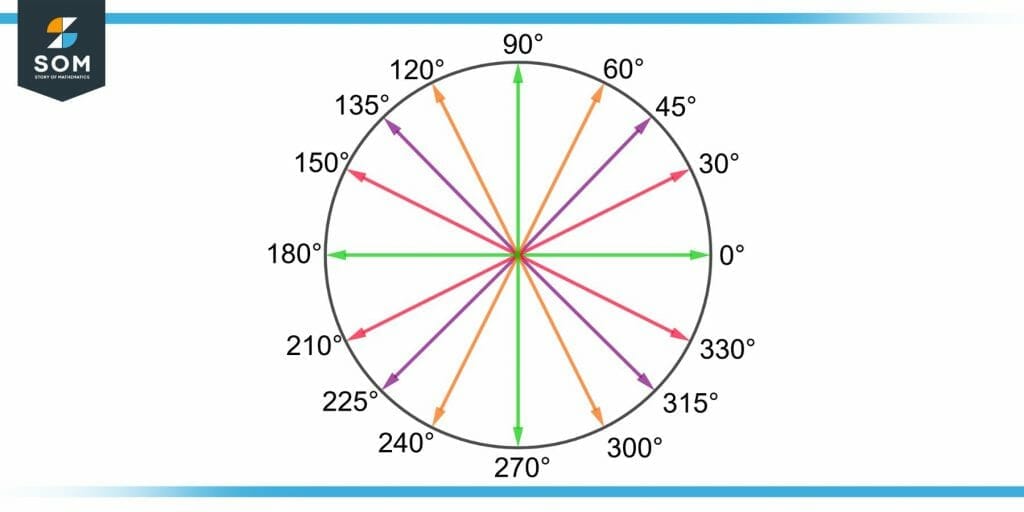
Figure 1 – Demonstration of Benchmark Angles
Introduction to the Terminology
The word “Benchmark” refers to a known standard that sets its values to be analyzed, compared, and measured against other values that are not commonly used.
An angle consists of two rays whose endpoints are joined at a point known as the vertex.
Types of Benchmark Angles
Benchmark angles play an essential role in trigonometry and can be divided into four major types. These are the quadrantal angles, the 30°, 45°, and 60° angles.
All the other benchmark angles are the reference angles of 30°, 45°, and 60° angles. These types of Benchmark angles are explained below.
Quadrantal Angles
Quadrantal angles are the angles whose one ray lies on the coordinate axes which are the x and y axes. They lie on the boundaries of the four quadrants.
These are 0°, 90°, 180°, and 270° with one ray lying on +x-axis, +y-axis, -x-axis, and -y-axis respectively. In radians, the quadrantal angles are 0, π/2, π, and 3π/2 rad.
The angles such as 360° co-terminal to 0° and other co-terminal angles are also considered quadrantal angles.
Figure 2 shows the four quadrantal angles.
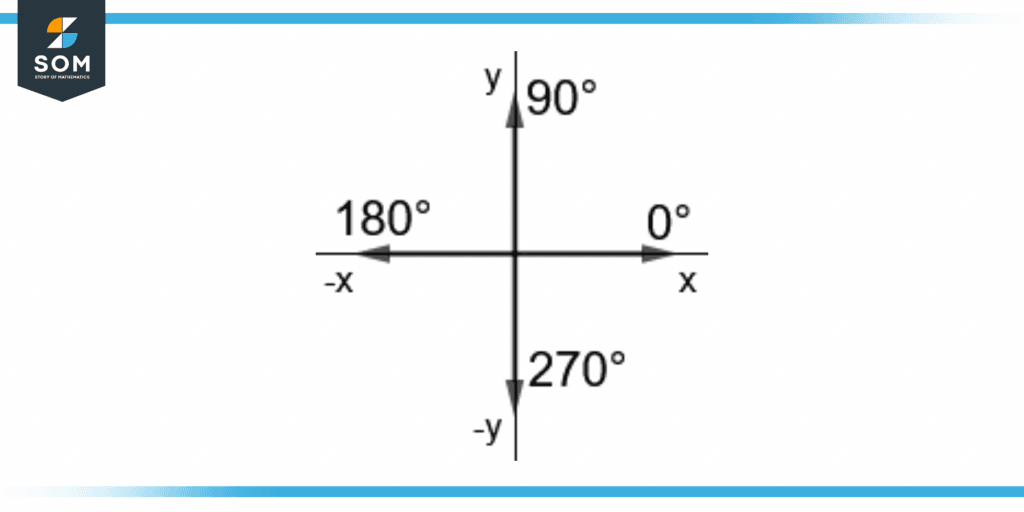
Figure 2 – Quadrantal Angles
The (cosine, sine) values for the quadrantal angles 0°, 90°, 180°, and 270° are (1,0), (0,1), (-1,0), and (0,-1) respectively.
30° Angle and Its Reference Angles
The 30° angle is a benchmark angle and is commonly used as a reference. It is equal to π/3 radians. It is an acute angle and lies in the first quadrant.
The reference angles of 30° are 150°, 210°, and 330° in the second, third and fourth quadrants.
In radians, these angles are equal to 5π/6, 7π/6, and 11π/6 rad respectively. These are obtained from the half (180°) or full (360°) rotation along a circle.
They can be written as follows:
150° = 180° – 30°
210° = 180° + 30°
330° = 360° – 30°
Benchmark angle of 30° and its reference angles are shown in figure 3.
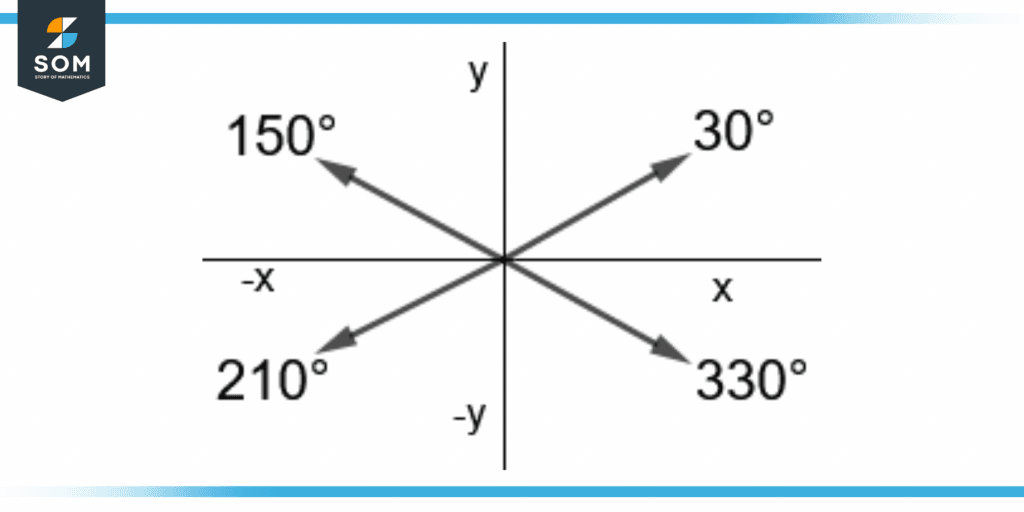
Figure 3 – 30° Angle With Its Reference Angles
45° Angle and Its Reference Angles
The 45° angle is acute and is also a benchmark angle. It is equal to π/4 radians and lies in the first quadrant.
The 45° angle has reference angles of 135°, 225°, and 315° in the second, third and fourth quadrants.
These are obtained by subtracting 45° from 180°, adding 45° to 180°, and subtracting 45° from 360°.
These reference angles can be written with the 45° angles as follows:
135° = 180° – 45°
225° = 180° + 45°
315° = 360° – 45°
The reference angles of 45° in radians are 3π/4, 5π/4, and 7π/4 rad. They are all the multiples of π/4 which is 45° in radians. These are shown in figure 4.
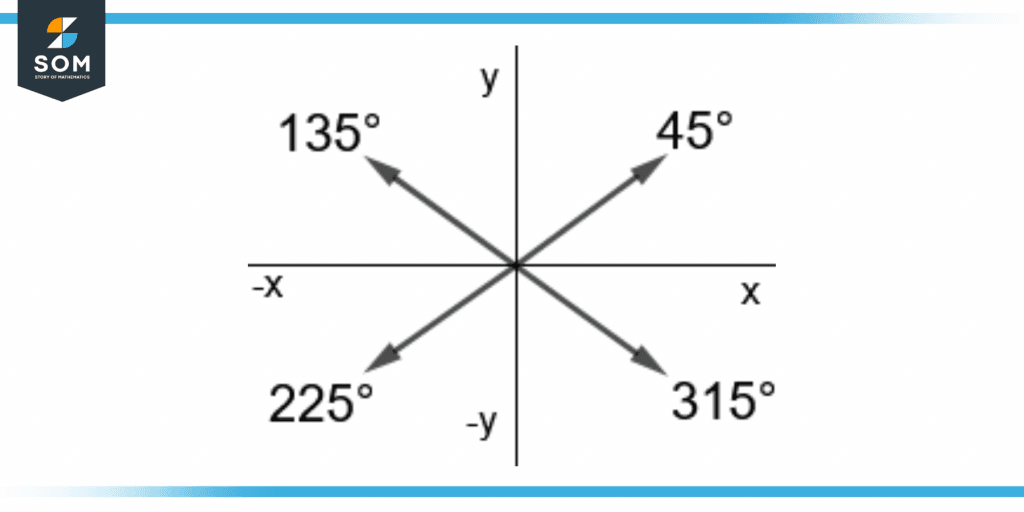
Figure 4 – 45° With Its Reference Angles
60° Angle and Its Reference Angles
The 60° angle is a benchmark angle and is commonly used in trigonometric calculations. It is equal to π/3 radians found in the first quadrant.
The reference angles of 60° degrees are 120°, 240°, and 300° degrees. They are also benchmark angles as they are used as a standard in different trigonometric problems.
They are equal to 2π/3, 4π/3, and 5π/3 radians. All have a common multiple of π/3 radians. The reference angles can be written with 60° degrees added or subtracted as follows:
120° = 180° – 60°
240° = 180° + 60°
300° = 360° – 60°
Figure 5 shows the angle of 60° along with its reference angles.
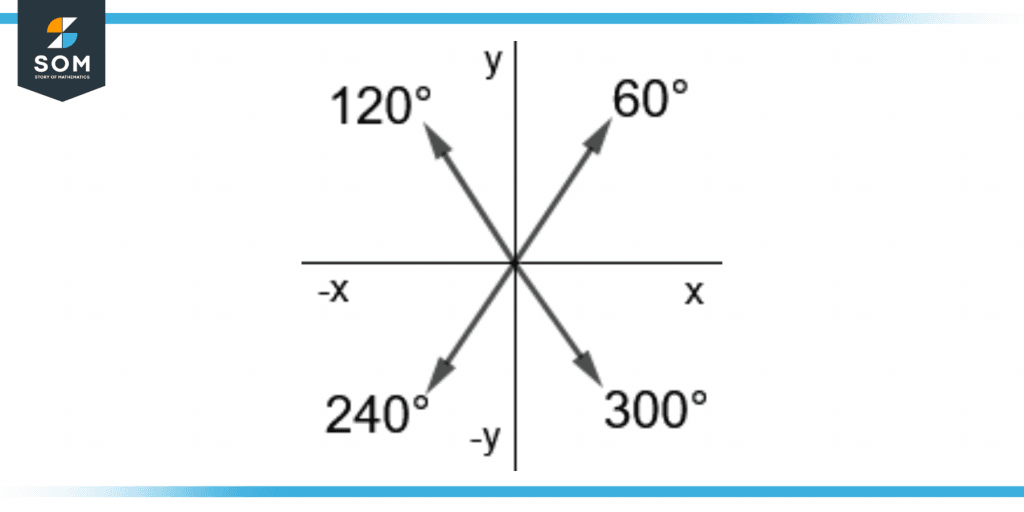
Figure 5 – 60° With Its Reference Angles
Use of Benchmark Angles
The benchmark angles are used in the approximation of acute angles and obtuse angles. This is done through the quadrantal benchmark angles which are 0° and 90°.
Approximating Acute Angles
Acute angles are such angles that lie between 0° and 90°. The benchmark angles 30°, 45°, and 60° are also acute angles. Any acute angle other than the benchmark angles can be approximated using the two quadrant angles 0° and 90°.
At first, the unknown angle is compared with the two quadrantal angles in such a way as to find which quadrantal angle is nearest to the unknown angle.
If the angle is near 0°, the angle can be estimated to be 15°. This is reasonable as it is near to 0° than to 90°. Figure 6 shows the approximated 15° angle lying near 0°.
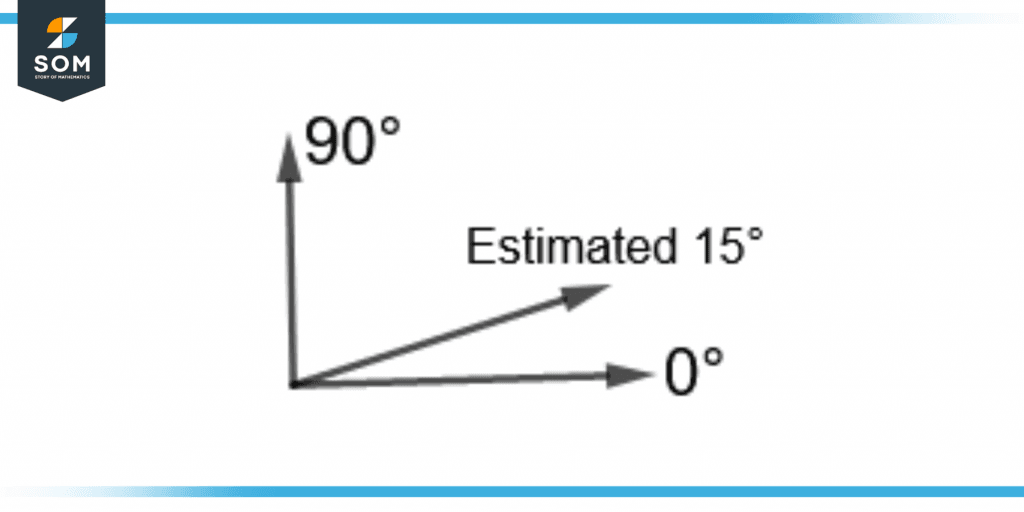
Figure 6 – Estimating 15° Through the 0° Benchmark Angle
Similarly, if the acute angle is closer to 90°, the angle can be estimated to be 85° as shown in figure 7.
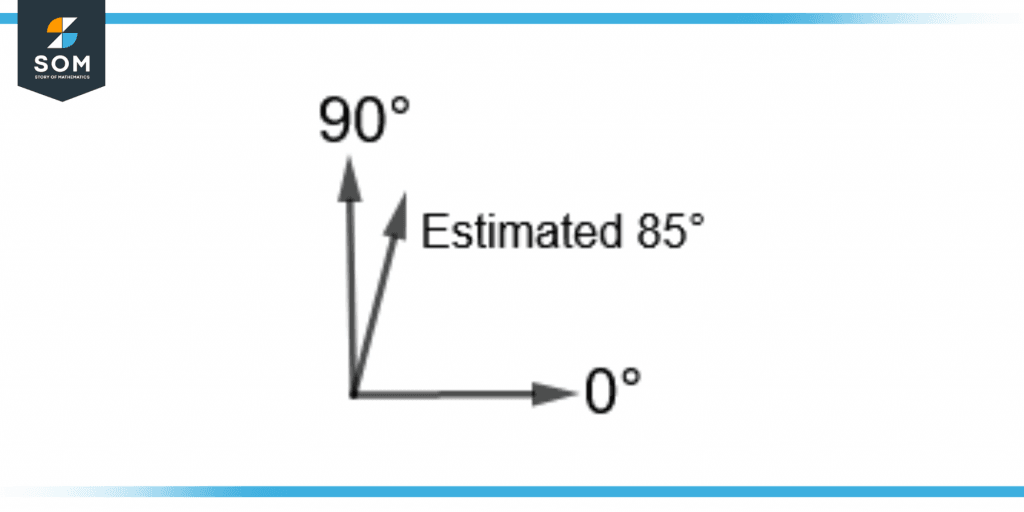
Figure 7 – Estimating 85° Through the 90° Benchmark Angle
Approximating Obtuse Angles
Obtuse angles are the angles present between 90° and 180°. The obtuse angles can be estimated by checking the closeness of the given angle to the two quadrantal angles, 90° and 180°.
For example, if the angle is closer to 90° and is obtuse, the estimated angle will be 100°. This is shown in figure 8.
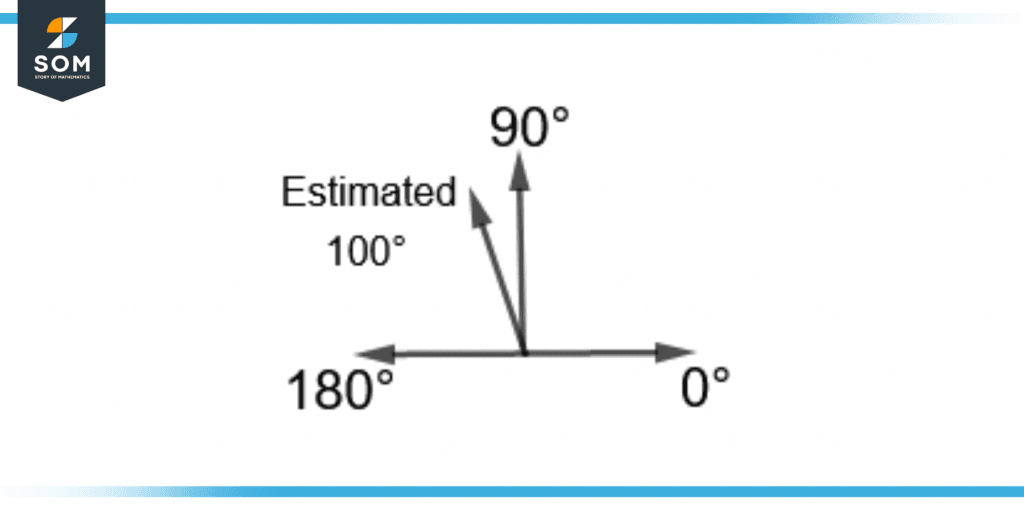
Figure 8 – Estimating 100° Through the 90° Benchmark Angle
These approximations help determine how large or small an angle is from the benchmark angles.
Using Benchmark Angles in a Problem
What is cos(A + B) if A and B are the benchmark angles where A = 30° and B = 60°? Also, prove the trigonometric property:
cos(A + B) = cos(A).cos(B) – sin(A).sin(B)
Solution
At first, putting the benchmark angles in cos(A + B) gives the result as follows:
cos(A + B) = cos(30° + 60°) = cos(90°) = 0
Now, putting the values on the right-hand side of the equation gives:
R.H.S = cos(A).cos(B) – sin(A).sin(B)
R.H.S = cos(30°).cos(60°) – sin(30°).sin(60°)
\[ R.H.S = \Big\{ \frac{ \sqrt{3} }{2} \Big\} . \Big\{ \frac{1}{2} \Big\} \ – \ \Big\{ \frac{1}{2} \Big\} .\Big\{ \frac{ \sqrt{3} }{2}\Big\} \]
\[ R.H.S = \Big\{ \frac{ \sqrt{3} }{4} \Big\} \ – \ \Big\{ \frac{ \sqrt{3} }{4} \Big\} \]
R.H.S = 0
As we can see that:
L.H.S = cos(A + B) = 0
L.H.S = R.H.S
Hence proved.
All the images are created using GeoGebra.
