Bias|Definition & Meaning

Bias is a word in statistics, that describes the direction of the measurement procedure. It means that it assesses the over or devaluation of the value of the population parameter. Consider an instance, you have the formula to estimate the mean of the population and you manage to find the measurement using the formula, which is the true examination of the population. Now, by utilizing the biased estimator, it is straightforward to see the difference between the actual value and the statistically predicted value of the population parameter. 

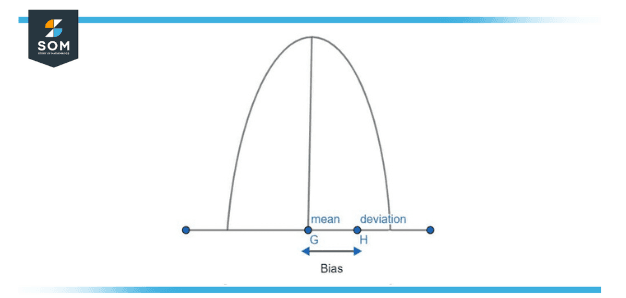
Figure 1 – Difference between the expected value and estimated value

There are many types of Bias in Statistics and are classified into two parts, that are The Measurement Bias and The Non-Representative Sampling Bias. Below we will discuss the classification of bias and its various kinds.

Understanding Bias

Bias in statistics is the discrepancy between the expected value of an estimator and its estimated value. Figure 1 for instance has a population mean value at point G. That means the expected value of the estimator is at point G. Now you take a sample from the population and compute its mean value and find out that your estimator has estimated the sample mean at point H. Actual value is G but your estimator has estimated H. so the difference between the actual value G and the estimated value H is bias. In simple terms, Bias is the deviation from the mean value.

Think of archery and consider that your bow is sighted inaccurately. High bias does not indicate you’re hitting all over the area but may provoke an excellent archer to strike below the bullseye all the spell. As in the below figure, the archer’s hits were accurate but because of high bias, he could not connect the yellow region.

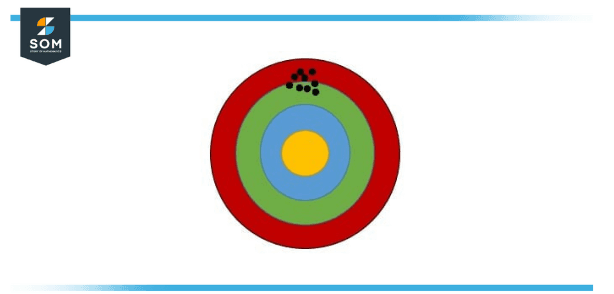
Figure 2 – High Bias Example

The below figure shows the sampling bias which refers to a biased sample induced by non-random sampling. To show an example, suppose that there are seven people in a chamber and you question if they like apples or bananas. If you only observe the three females and infer that most people like apples, you’d have demonstrated sampling bias because you have not observed any male preference.

Figure 3 – Bias Sampling Error Example

Measurement Bias

Measurement bias takes place for the whole duration when holding out a survey, and the causes for its impacts because of the following;

1. The Error Takes Place Solely When Recording Data.

When registering any data, we obtain errors because of the malfunction of the tools used for reading data,  or, also due to the weak handling of the instruments by the data collection individuals.

2. Leading Questions for the survey.

Preparations of the questioning that are needed for the survey might be placed in a way that is interviewer-friendly,  responses will be according to the interests of the interviewer, and queries that will be responded to which are desired by the interviewer/researcher. There must be more preferences for them to get a decent report.

3. False Responses from Respondents.

Circumstances can arise when numerous responders misinterpret the questions and provide an incorrect answers. In the care of older respondents, when they are envisioned to fill the survey responses by remembering their earlier experiences, this may cause further misconception and this could bring incorrect inputs due to weakly record keeping

Non-Representative Bias

This happens when a survey model represents the population incorrectly, which is due to operating involuntarily with only an exact split of the population, and here the representative becomes unrepresentative of the entire population. The main types of selection bias are:

Undercoverage Bias happens when some respondents of the instance population are not wholly illustrated. The reasoning behind such a bias is the comfort of sampling, that takes place when the information is collected from an easily available source. An instance can be the local supermarket.

Non-response Bias happens when the people who are identified to designate a survey are reluctant or unable to take place in the survey. In this matter, the respondents have an upper hand over the survey’s outcome.

Voluntary response bias happens when members who bring samples are self-selected volunteers. These Answers give a faulty and wrong illustration of the general population who are in acceptance of strong opinions.

Survivorship Bias directs to that type of survey that calls for the survival of a long procedure for being measured as a complete response that offers a rise in biased sampling.

Bias as an Estimator

The bias of an estimator (bias function) in statistics,  is the distinction between this estimator’s predicted value and the true value of the parameter being evaluated. The unbiased estimator is an estimator for finding rules with zero bias. In statistics, bias is an accurate property of an estimator. Bias is a separate idea from consistency. Uniform estimators join in probability to the actual value of the parameter but may be unbiased or biased.

All others being equal, an unbiased estimator is preferable over a biased estimator, although, in reality, biased estimators with slight biases are often used. When a biased estimator is utilized, the bounds of the bias are computed. A biased estimator may be operated for various causes, or because an unbiased estimator doesn’t exist without additional inferences about a population or because an estimator is complex to estimate, or because a biased estimator might be unbiased with regard to different measurements of the main tendency, or because a biased estimator offers a lower value of little loss function resembled with unbiased estimators or because in some scenarios being unbiased is too robust a condition, and the singular unbiased estimators are not applicable.

Solving Problem – Bias

Example 1

Source of bias in which the population chooses to answer and commonly only people with very firm opinions answer.

A. Response Bias

B. Undercoverage

C. Convenience Sampling

D. Voluntary Response

Solution

Answer:

D. Voluntary Response

Example 2