Binomial|Definition & Meaning

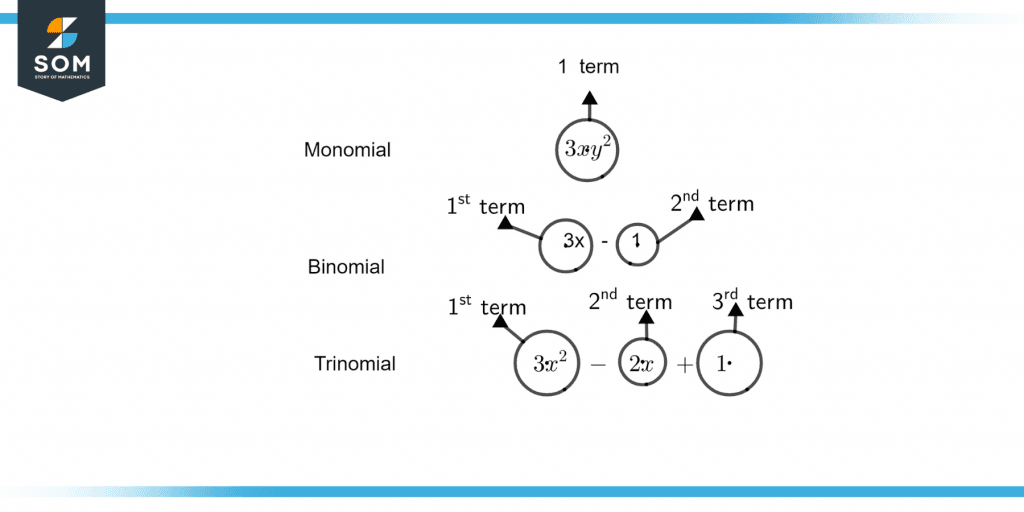
Figure 1 – Difference between monomial, binomial, and trinomial

Figure 1 illustrates the difference between Monomial, Binomial and Trinomial. 

A polynomial called a binomial has just terms. As an illustration, x + 2 is a binomial, where x and 2 are two distinct words. Additionally, in this case, x’s exponent, coefficient, and constant are all equal to 1. A binomial is an algebraic statement with two terms that comprises a variable, a coefficient, exponents, and a constant.

Using variables and coefficients, polynomials are algebraic expressions. The word “indeterminates” is sometimes used to describe variables. For polynomial expressions, addition, subtraction, multiplication, and positive integer exponents are all mathematical operations that are possible. However, division by variables is not one of them.

Since the Greek words “polynomial” and “nominal” both imply “terms,” the phrase “many terms” may be translated from the word polynomial. Any number of terms, but not infinite ones, can be found in a polynomial.

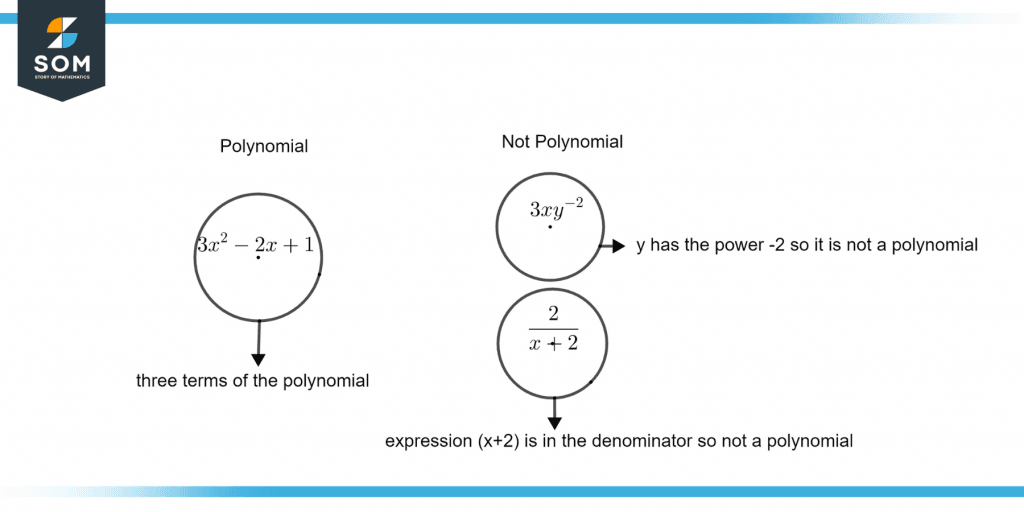
Figure 2 – Difference between polynomial and non-polynomial expression

Figure 2 illustrates the difference between Polynomial and non-polynomial expressions.

Binomial is the name for an algebraic expression with only two terms. It is a polynomial with two terms. It is sometimes referred to as the sum or difference of two or more monomials. It is a polynomial’s most basic form.

A binomial can be written as a single indeterminate as follows: ax^m + bxⁿ. Where m and n are non-negative distinct integers and a and b are the numbers. X can be a variable or indefinite.

Binomials are stated in the same way in Laurent polynomials; the main distinction is that m and n may have negative exponents. Consequently, we may express it as ax^-m + bx^-n.

Mathematical Operations on Binomials

There can be many mathematical operations that can be performed on Binomial like Factorization, addition, subtraction, multiplication, raising to the nth power, and conversion to lower-order binomials.

Factorization of Binomials

A binomial can be factored and written as the sum of the other two. For instance, (x + y)(x – y) may be used to represent x² – y².

Addition of Binomials

Only when two binomials contain similar words may they be added. This implies that the variable and exponent should be the same. For instance, Let’s think about two equations. 9x³ + 6y and 10x³ + 4y. Adding the two solutions to the equation (10x³ + 4y) and (9x³ + 6y). The resulting equation is thus = 19x³ + 10y.

Subtraction of Binomials

When and only when it includes like words, the addition operation of two binomials and their subtraction are analogous. Examples include 12x³ + 4y and 9x³ + 10y. When the aforementioned polynomials are subtracted, the result is (12x³ + 4y) – (9x³ + 10y) = 12x³ + 4y – 9x³ – 10y. The resulting equation is thus = 3x³ – 6y.

Multiplication of Binomials

Using the distributive property, two binomials are multiplied, resulting in four terms. The FOIL approach is how it’s often known. Since each term of the first factor is multiplied by the second factor in this technique, multiplication is accomplished. Thus, a trinomial is used to represent the result of multiplying two two-term polynomials.

Raising to the n’th Power

When a binomial is raised to the nth power, it may be written as: (x + y)ⁿ.

Conversion to Lower-order Binomials

Any higher-order binomial may be factored down to a lower-order one, such as cubes can be factored down to the products of squares and another monomial.

Binomial Theorem

The term “binomial theorem” or “binomial expansion” refers to the algebraic expansion of a binomial’s powers in elementary mathematics. The theory states that the polynomial (x + y)ⁿ may be expanded into a sum comprising terms of the type ax^by^c, where the exponents b and c are non-negative integers with b + c = n and the coefficient an of each term is a particular positive integer dependent on n and b.

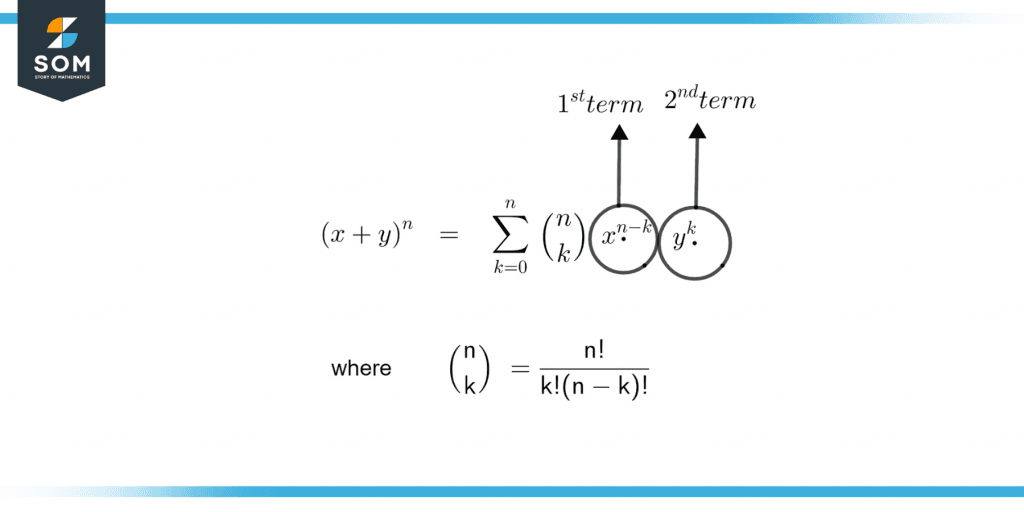
Figure 3 – Binomial expansion

Figure 3 illustrates the formula for Binomial Expansion.

At least since the Greek mathematician Euclid noted the particular case of the binomial theorem with exponent 2 in the fourth century BC, specific instances of the binomial theorem have been known. There is evidence that the cube binomial theorem was understood in India by the sixth century AD.

The number of ways you can choose k items from a total set of n without replacing them is expressed as binomial coefficients, which are combinatorial numbers of importance to ancient Indian mathematicians. The Chandastra by the Indian poet Pingala (about 200 BC), which includes a technique for its resolution, is the first recorded mention of this combinatorial problem.

According to our understanding, Al-book, Karaji’s, which was cited by Al-Samaw’al in his “al-Bahir,” contains the earliest statement of the binomial theorem as well as the table of binomial coefficients.

Using an early form of mathematical induction, Al-Karaji explained the triangular arrangement of the binomial coefficients and offered a mathematical proof for both Pascal’s triangle and the binomial theorem.

Omar Khayyam was a mathematician and poet from Persia, and it’s likely that he was aware of the formula to higher levels even if much of his mathematical writings had been destroyed. The 13th-century mathematical writings of Yang Hui and Chu Shih-Chieh provide information on binomial expansions of tiny degrees.

Although such works are now also widely available, Yang Hui claims that Jia Xian wrote the approach in a far older document from the 11th century.

Some Examples of Binomials

Example 1

Solve the following for the value of x:

a) 3x – 9

b) x² – 2x + 1

c) x² – 6x + 9

Solution

a) In order to evaluate the value of x for the polynomial, we will put this equation equal to zero, i.e.:

3x – 9 = 0

3x = 9

x = 9/3

x = 3

b) In order to evaluate the value of x for the polynomial, we will put this equation equal to zero, i.e., then we will factorize:

x² – 2x + 1

x² – x – x + 1

Now we will take x and 1 common from the equation:

x(x – 1) – 1(x – 1)

(x – 1)(x – 1)

x = 1

c) In order to evaluate the value of x for the polynomial, we will put this equation equal to zero, i.e., then we will factorize:

x² – 6x + 9

x² – 3x – 3x + 9

Now we will take x and 3 common from the equation:

x(x – 3) – 3(x – 3)

(x – 3)(x – 3)

x = 3

Example 2

Add the following polynomials

3a + 2b + 6c , 2a + 3b and a + 3b + 2c

Solution

In order to add the polynomials, we will add all the like terms, such as the terms with ‘a’ as a coefficient, the terms with b, and so on:

3a + 2b + 6c + 2a + 3b + a + 3b + 2c

3a + 2a + a + 2b + 3b + 6c + 2c

6a + 5b + 8c

All images were created using GeoGebra.

Bias Definition < Glossary Index > Bisect Definition