Bisect|Definition & Meaning

Consider the line segment $\mathsf{\overline{AB}}$ of length 20 cm. Cutting the line segment at its midpoint J guarantees that the split parts $\mathsf{\overline{AJ}}$ and $\mathsf{\overline{JB}}$ will have the same length of 20/2 = 10 cm. We illustrate this fact in the following figure: 

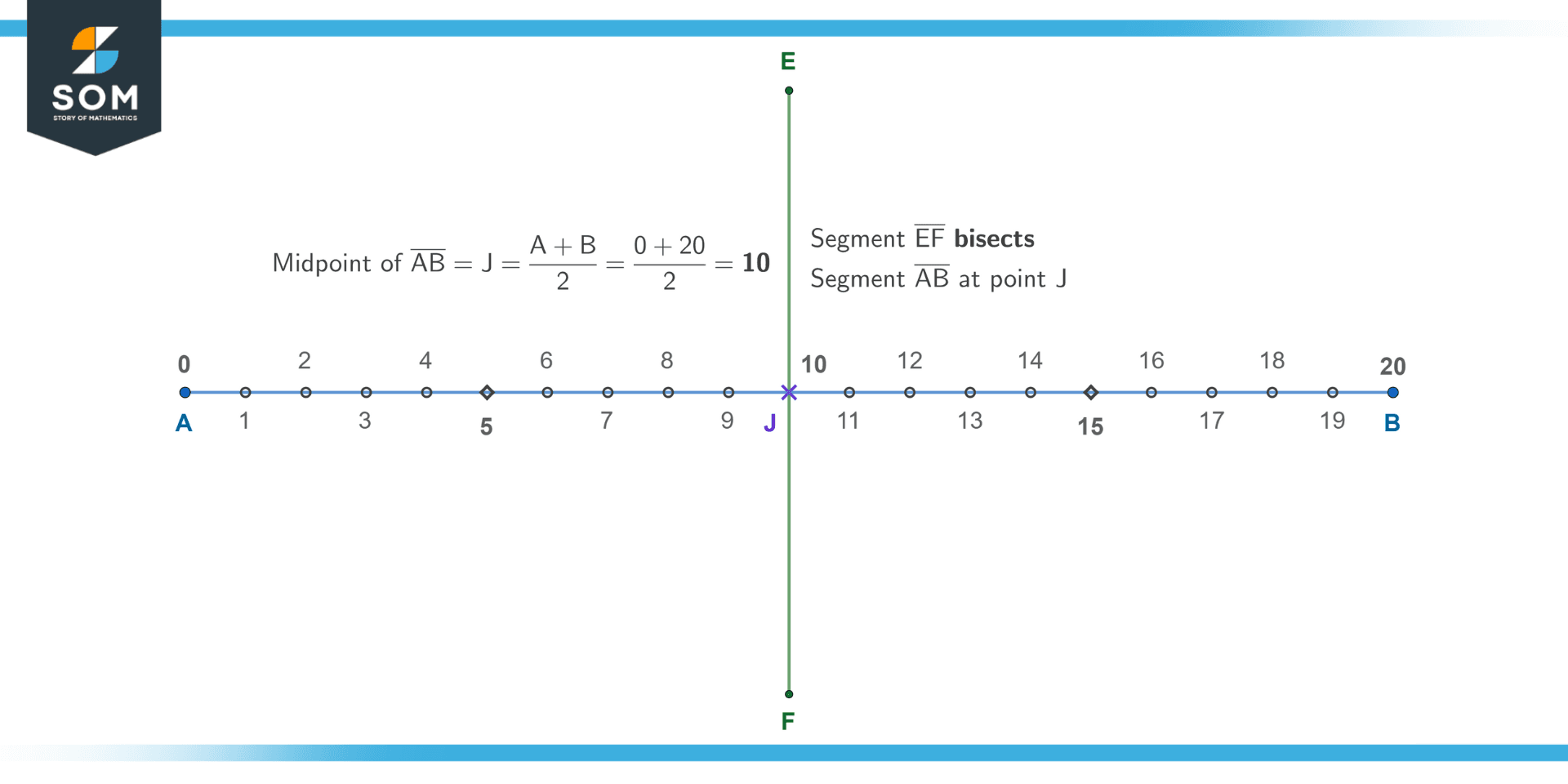
Figure 1 – Bisecting a line segment with another one passing through its midpoint.

Note how bisection is essentially a division by 2. For example, if an angle of 30 degrees is bisected, the two split angles are 30/2 = 15 degrees each. Similarly, if a line segment of 10 cm is bisected, the two pieces have a length of 10/2 = 5 cm each.

Conditions for Bisection

The only necessary condition for a bisection is that the two split parts are of equal length or magnitude. You can bisect angles, lines, planes, curves, etc., with other geometrical shapes and objects. The bisecting shape or object is called the bisector. 

Notice that this is contrary to an intersection, which only requires two geometrical objects to cut into each other at some common point called the vertex. Therefore, every bisection is an intersection (by definition), but every intersection is not a bisection. The following figure illustrates this difference:

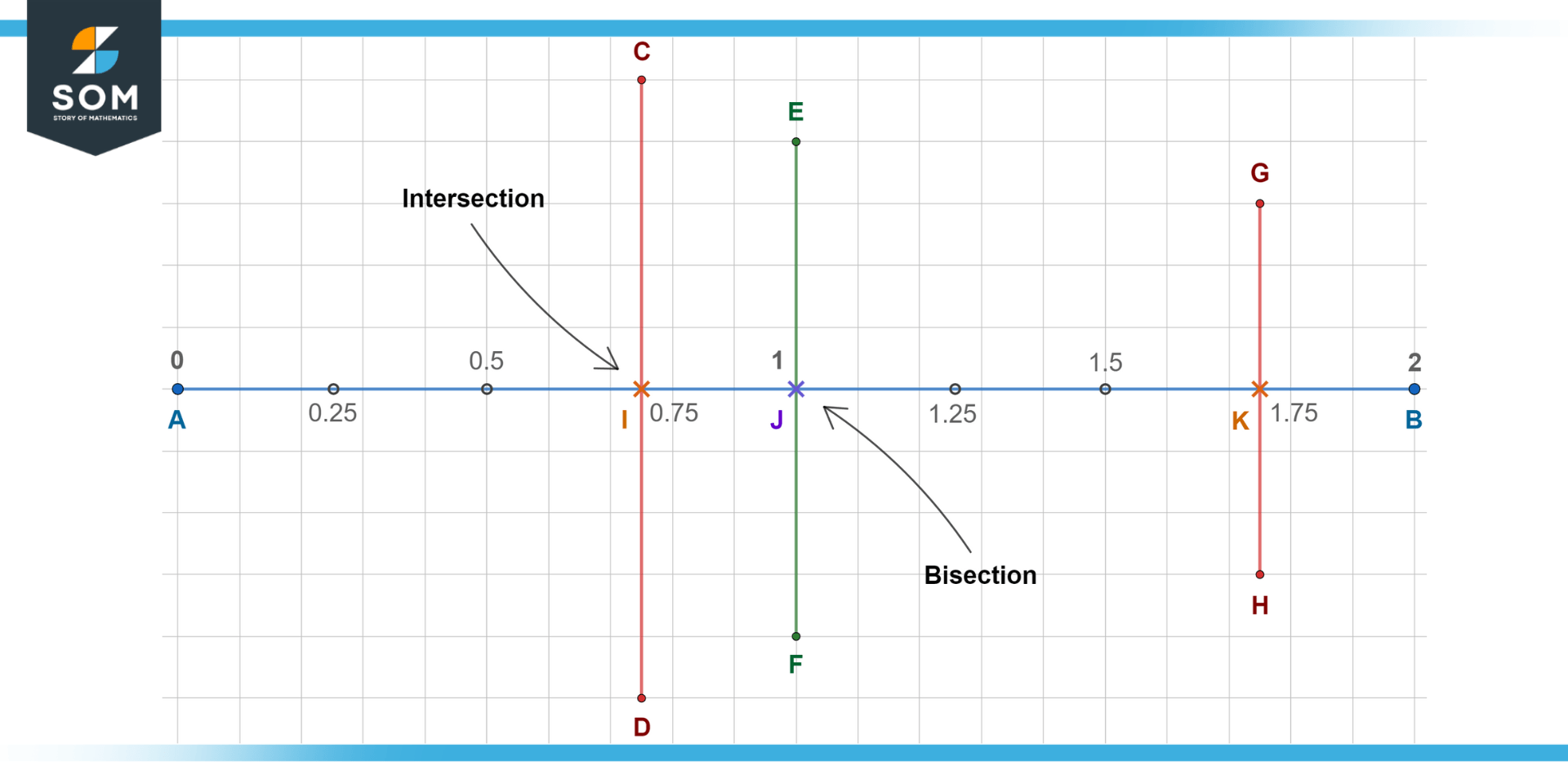
Figure 2 – Highlighting the difference between an intersecting and bisecting line segment.

Here, segment $\mathsf{\overline{AB}}$ is intersected by segments $\mathsf{\overline{CD}}$, $\mathsf{\overline{EF}}$, and $\mathsf{\overline{GH}}$. However, only $\mathsf{\boldsymbol{\overline{EF}}}$ is the bisector, while the others are not (i.e., they do not split the segment $\mathsf{\overline{AB}}$ into equal parts).

Bisecting Lines and Segments

For a line segment with two finite endpoints, any object intersecting its midpoint is a bisector of that line segment. You can see this in Figure 1 from the definition.

If the bisector cuts into the line segment at a right angle, it is called a perpendicular bisector. It is also possible for a line segment to have multiple bisectors. For example, see the figure below:

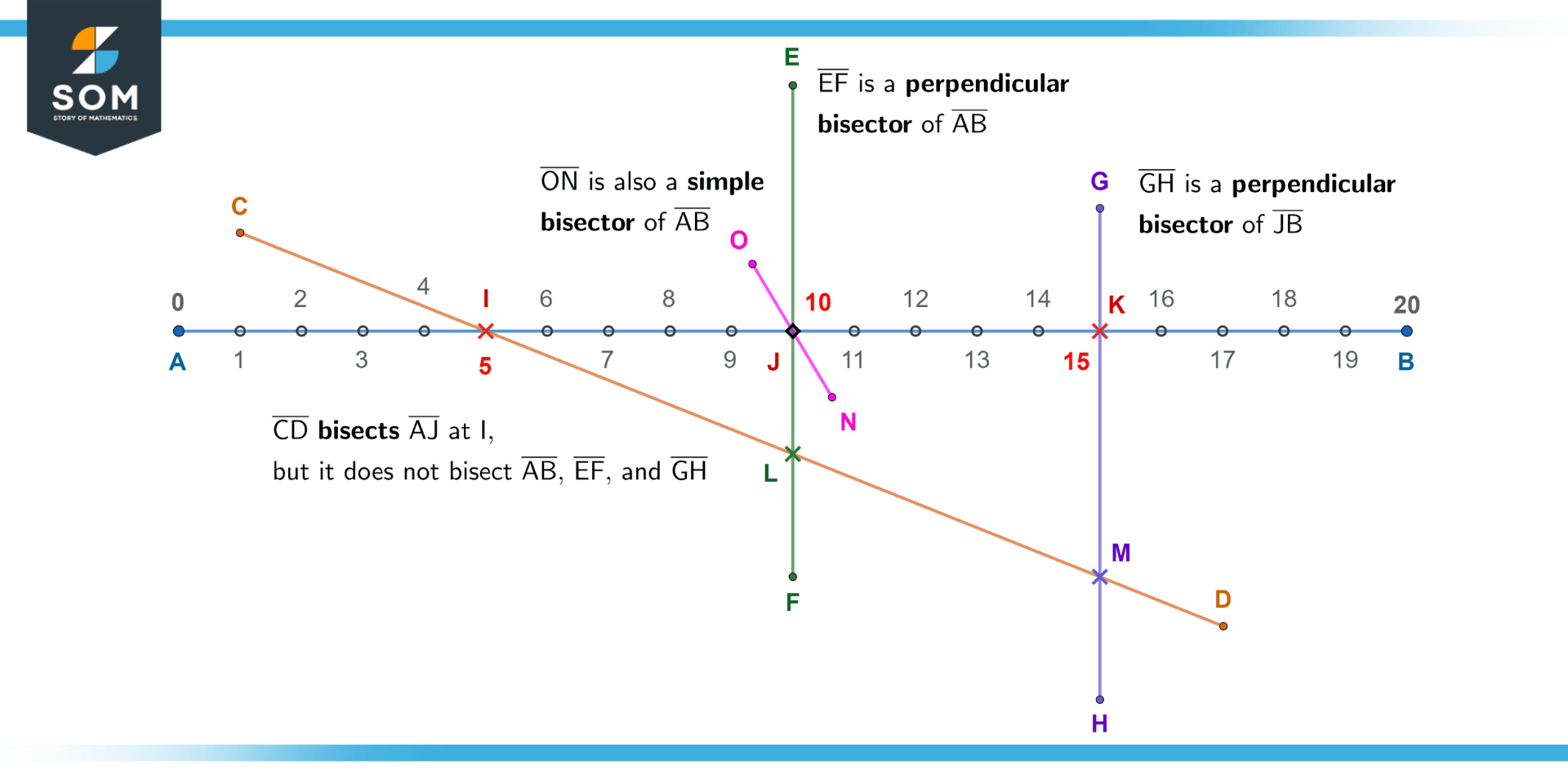
Figure 3 – A line segment can have multiple bisectors, and it is also possible that a segment bisects only a part of a segment.

Here, segments $\mathsf{\overline{EF}}$ and $\mathsf{\overline{ON}}$ are both bisecting the segment $\mathsf{\overline{AB}}$. However, note that $\mathsf{\overline{EF}}$ is a perpendicular bisector, while $\mathsf{\overline{ON}}$ is not.

Further, while $\mathsf{\overline{CD}}$ does not bisect $\mathsf{\overline{AB}}$, it bisects the (bisected) part $\mathsf{\overline{AJ}}$ at midpoint I.

Bisecting Angles

We illustrate an angle bisector in the following figure:

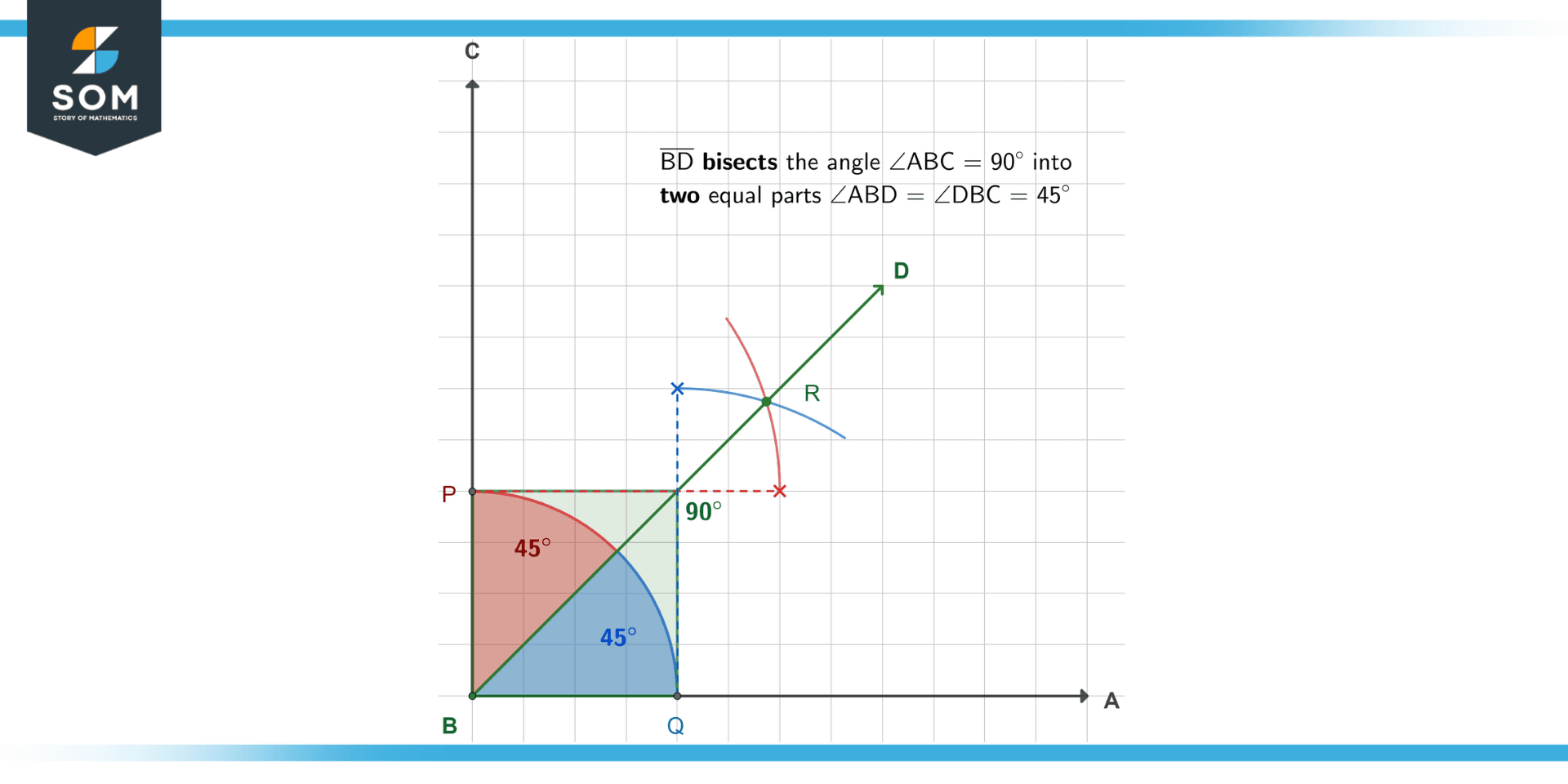
Figure 4 – Angle bisection using the compass method.

Here, the angle of 90 degrees between the two rays $\mathsf{\overrightarrow{BC}}$ and $\mathsf{\overrightarrow{BA}}$ is colored green. The ray $\mathsf{\overrightarrow{BD}}$ (or you can also use a segment) bisects this angle $\mathsf{\angle{ABC}}$ into two halves ($\mathsf{\angle{ABD}}$ and $\mathsf{\angle{DBC}}$) of 45 degrees each, respectively colored blue and red. 

To bisect an angle between two given rays, you have two methods. 

The first is to use a protractor to measure the angle between the rays. Then, with the protractor’s center placed at the vertex, mark the angle half of the measured one. Finally, join the vertex and the marked point. This line bisects the angle!

The second method does not require measuring angles. Yet, it guarantees that the resulting line bisects the angle. Figure 4 visualizes this method.

You will need a compass and ruler: fix the compass on the vertex, open it up to a convenient radius, and draw an arc that cuts both rays. Let us call these intersection points P and Q. 

Now, fix the compass on either P or Q and open it up however you want; it does not matter here. Then, draw an arc roughly sandwiched in between the two rays. Now, without changing the compass opening, fix it on the other point (Q or P) and draw an arc that intersects the one from the previous step. Let us call this intersection R.

Join the vertex of the rays and R to form a line that bisects the angle!

Why Is Bisecting Important?

Bisection forms the basis of several geometrical concepts and theorems. For example, it is a core requirement for understanding the concept of median, centroid, and circumcenter. All of these involve bisection in some way.

A median refers to a line segment joining a vertex of a triangle to the midpoint of the opposite side. As such, a median is a bisector of that opposite side. The point of intersection of all the medians is the centroid of a triangle, which is very important as it defines the center of mass of that triangle (if it is uniform).

The circumcenter is a bit more complex. It defines the point where, if you place a compass and extend it to any one of the triangle’s vertices and draw a circle, it would pass through all the three vertices of the triangle. The resulting circle is called the circumcircle, and the circumcenter is therefore its center.

Interestingly, the circumcenter is constructed by finding the point where the perpendicular bisectors of all three sides of a triangle intersect.

Additionally, bisectors of polygons like the Rhombus and conic sections like the parabola impart various properties to these shapes, leading to many interesting facts and theorems which greatly simplify their analysis.

Bisection also has complex applications: the construction of repeated lattice structures (e.g., Weigner-Seitz) in chemistry, the formation of the excircle and Thales’ circle, and Voronoi diagrams. 

An Example of Finding Bisectors

Continually bisect the given line segment $\mathsf{\overline{XZ}}$ into four equal parts. Assume all lengths are in centimeters (cm).

Solution

From the figure, we can see that the midpoint P of the segment $\mathsf{\overline{XZ}}$ is:

P = (5 + 10) / 2 = 7.5

Therefore, we first draw a perpendicular bisector through $\mathsf{\overline{XZ}}$ on point P. Now we have two equal segments $\mathsf{\overline{XP}}$ and $\mathsf{\overline{PZ}}$ with length 2.5 cm (since 7.5 – 5 and 10 – 7.5 = 2.5). Let the midpoints of $\mathsf{\overline{XP}}$ and $\mathsf{\overline{PZ}}$ be Q and R, then:

Q = (5 + 7.5) / 2 =  6.25

R = (7.5 + 10) / 2 = 8.75

We draw two perpendicular bisectors through Q and R. 

The segment $\mathsf{\overline{XZ}}$ is thus divided into four equal parts $\mathsf{\overline{XQ}}$ (6.25 – 5 = 1.25 cm), $\mathsf{\overline{QP}}$ (7.5 – 6.25 = 1.25 cm), $\mathsf{\overline{PR}}$ (8.75 – 7.5 = 1.25 cm), and $\mathsf{\overline{RZ}}$ (10 – 8.75 = 1.25 cm).

The resulting figure looks like this:

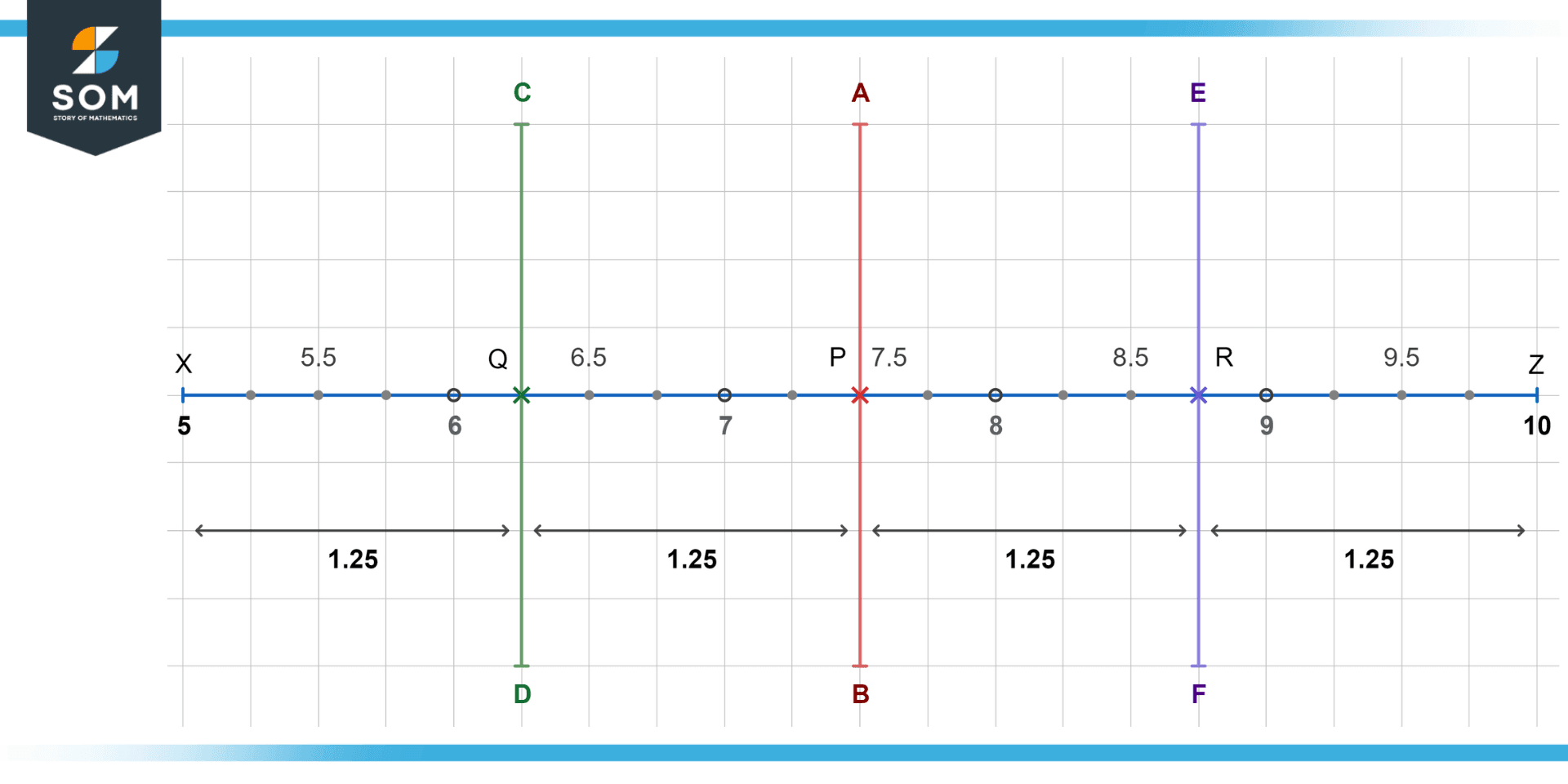
Figure 5 – Bisecting a line into four equal parts.

All mathematical drawings and images were created with GeoGebra.

Binomial Definition < Glossary Index > Bisector Definiton