JUMP TO TOPIC
Bisector|Definition & Meaning
Definition
In geometry, a bisector is any shape or line that cuts a line segment, an angle, or a curve into two equal parts. This can be explained by bisecting a line segment using a bisector, where a line cuts a line segment AB into two equal pieces. It means that the line segment is bisected, that is, split into two equal parts. A similar case can be considered where an angle is bisected using a line segment.
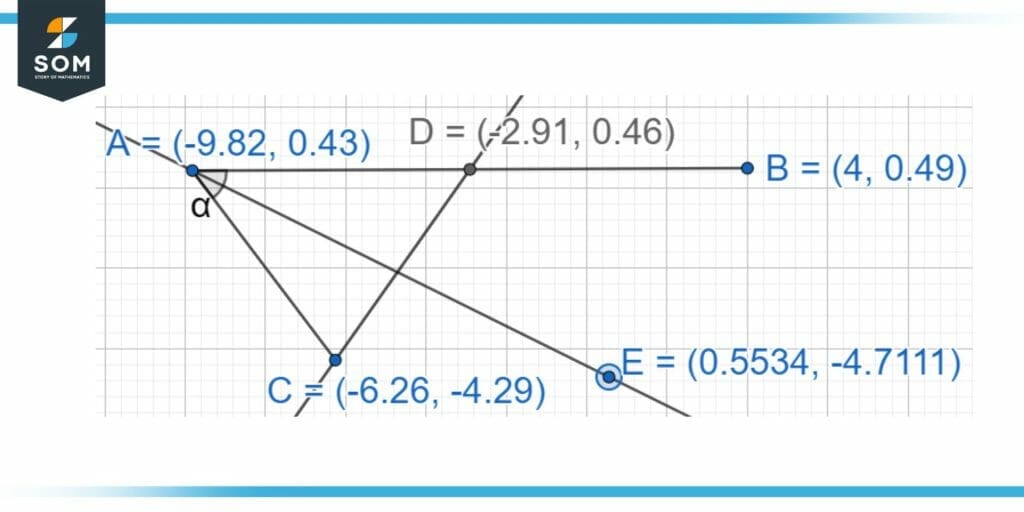
Figure 1: Line AB is bisected by a bisector crossing through line CD and the ∠BAC is bisected by an angle bisector passing through line AE.
Furthermore, a bisector can also be in the form of a 3-D plane. This plane cuts another 3-D plane into two equal and symmetrical parts. There are multiple types of bisectors in geometry.
A bisector can cut a line segment at any angle to the line segment given that it divides the line into two equal parts. A bisector that is perpendicular to the line segment that is getting bisected is called a perpendicular bisector.
A line that slices an angle formed by two adjacent lines equally is known as an angle bisector. This signifies that the angle is formed by two intersecting lines or by three points A, B, and C, with the angle formed by two line segments, split in half by an angle bisector DB, where D is a point on the graph.
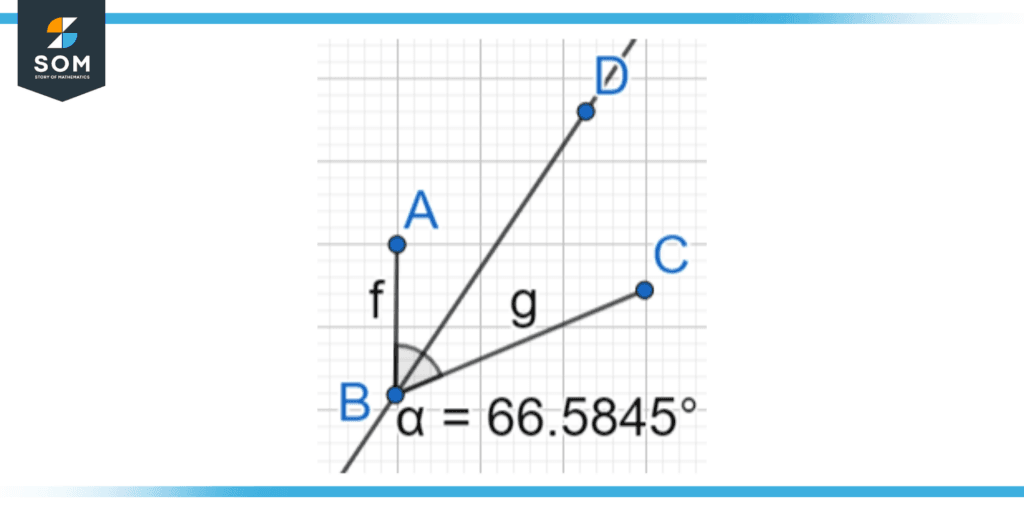
Figure 2: An Angle bisector used to cut ∠ABC = 66.5845 into half.
Different Cases of Application of a Bisector and Their Construction
Let us consider we are given a line AB that is 10 centimeters long. If we use a bisector at any angle across this line AB, it will intersect the line at a midpoint M and divide the line segment into two lines namely line AM and MB. These two lines will be half of the original length which is 5 cm. Hence, a bisector is very helpful in dividing a line segment into equal parts.
In another case, let us say we have two adjacent line segments AB and BC making an angle of 80°. This ∠ABC can be cut into half as per our requirements by drawing an angle bisector. This can be done by drawing two arcs from the same distance on the line segment from the origin point B into the middle of the two line segments.
The intersecting point between these two arcs will decide the point D and the line segment BD will be our angle bisector. This can be easily done with the help of a compass.
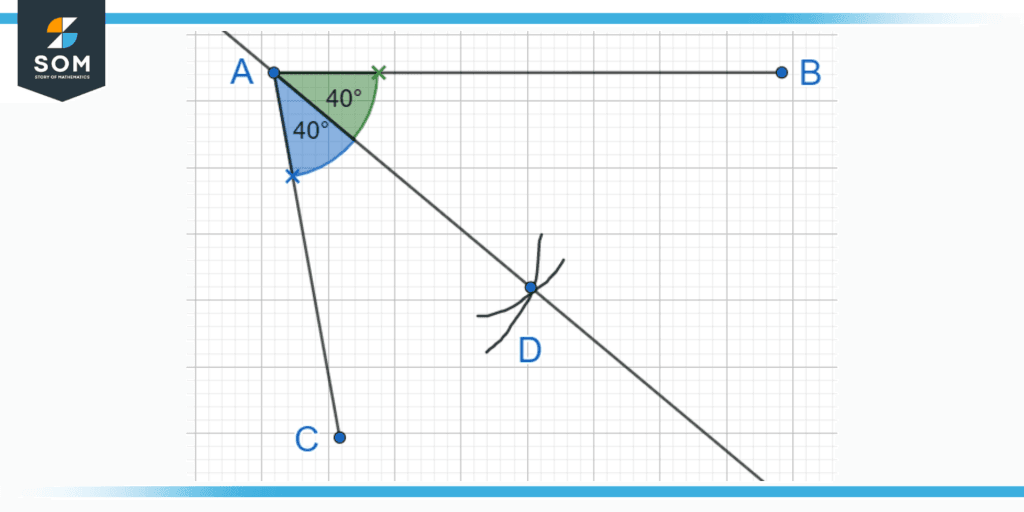
Figure 3: The angle bisector BD cutting the ∠ABC = 80° into two angles of 40°.
Furthermore, a perpendicular bisector can also be easily constructed using a compass and a ruler. Firstly, you need to draw two arcs of a specific radius using a compass on each side of the line segment with the center being the end of the line segment. The same arcs are then drawn again from the other side of the line segment is the center of the arc.
The arcs intersect at two points, one on each side of the line segment. Then all you need is to draw a straight line through the two points. The resulting line is the perpendicular bisector of the corresponding line segment.
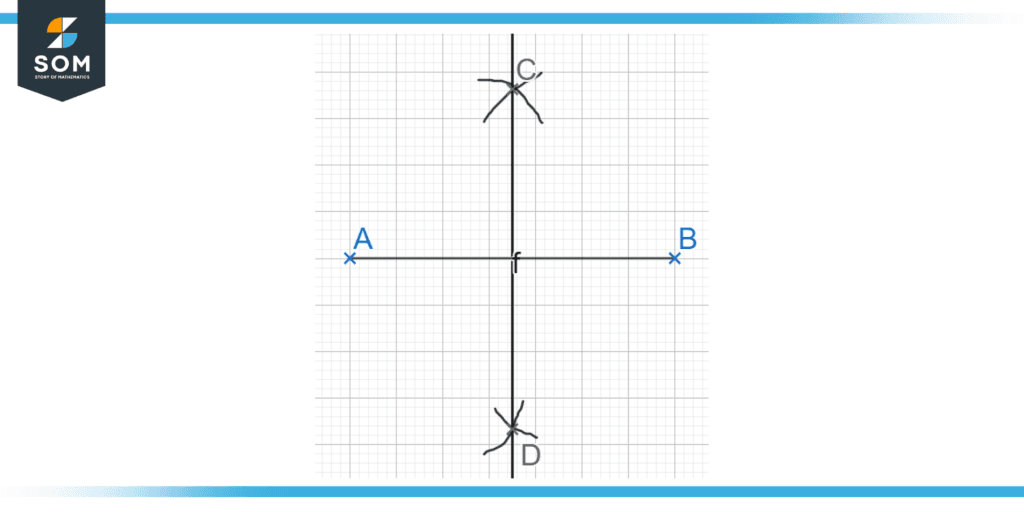
Figure 4: A perpendicular bisector CD constructed for Line AB with the use of a compass and a ruler.
Significance of a Bisector in Geometry and Advanced Real-Life Applications
A bisector is of utter importance in many geometrical theorems and is fundamental to many concepts in geometry. Most commonly, triangular properties can be easily found by finding its centroid, median, incenter, and circumcenter and bisectors play an important part in finding these properties.
The section connecting a vertex to the middle of the other side is known as a triangle’s median. A median is hence a bisector of that opposing side. The centroid of a triangle is the place where all of the medians connect, and this is particularly significant since it establishes the triangle’s center of mass, given that the triangle is uniform.
The circumcenter is the center of the circle (also known as the circumcircle) that goes across the triangle’s three vertices. Furthermore, the circumcenter is also the intersecting point of all three perpendicular bisectors that bisect each side of the triangle.
Moreover, a circle enclosed inside the triangle has a center point that can be found by intersecting all three of the angle bisectors of each vertex of the triangle. This is called the incenter of the triangle.
The centroid, circumcenter, and incenter of the triangle are three of the four common centers of a triangle that are used to define the property of a given triangular figure. They all differ in the type of bisectors used, and their intersection points define that center.
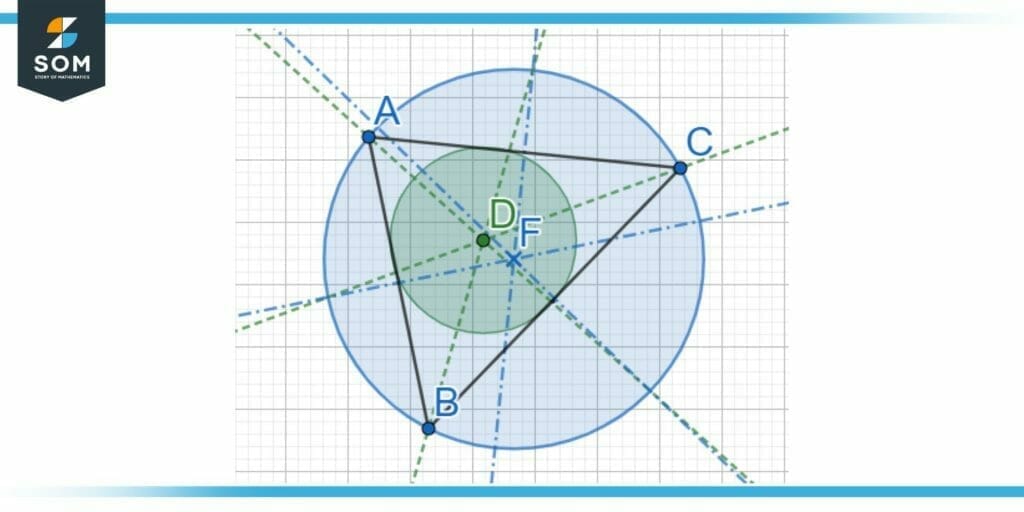
Figure 5: The circumcircle and the incircle of a triangle.
In figure 5 above, the blue circle is the circumcircle that has a circumcentre at point F, which is made by the intersection of perpendicular bisectors. The green circle inside the triangle has a center at the incenter of the triangle at point D, made by the intersection of the angle bisectors of the triangle.
An Example of Calculating a Bisector of a Line Segment
Given is a line AB of length 20 centimeters. Divide this line into four equal pieces by drawing perpendicular bisectors across it.
Solution
The midpoint M of the line AB can be calculated as follows:
\[ M = \frac{(20 + 0) }{2} \]
\[ \mathbf{M = 10 cm}\]
Thus, we will draw a perpendicular line at point M that will be our first bisector, and two line segments AM and MB are formed. We will find the midpoints of these two line segments P and Q to divide them further into two more equal parts.
\[ P = \frac{(10 + 0) }{2} \]
\[ \mathbf{P = 5 cm}\]
\[ Q = \frac{(20 + 10) }{2} \]
\[ \mathbf{Q = 15 cm}\]
Hence, we will now draw a perpendicular line across the points P and Q at the 5 cm and 15 cm mark respectively. Thus we are given a line segment AB that is divided equally into 4 parts.
All mathematical drawings and images were created with GeoGebra.
