Boundary|Definition & Meaning

A boundary allows us to identify the shape of an object or image and is necessary for separating one shape from another. 

Visualizing a Boundary

Figure 1 below shows a rectangle ABCD. The lines between the points ABCD is known as the boundary. With the help of the boundary, we can easily distinguish the shape.

Figure 1 – Boundary of a rectangle.

Figure 2 below shows the points EFG; as in the previous figure, these points are connected with a boundary that gives it its shape. The figure is called a triangle.

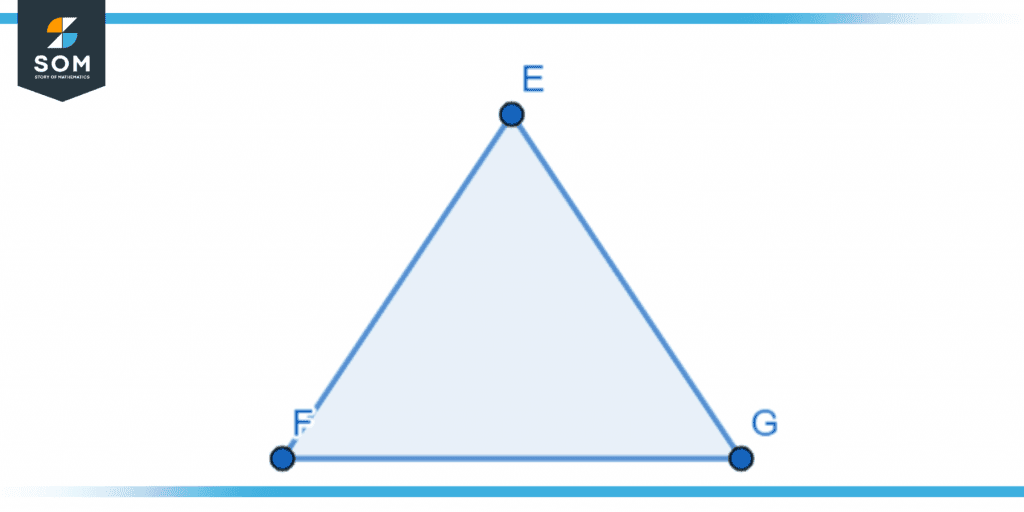
Figure 2 – Boundary of a triangle.

What Is a Perimeter?

The perimeter of any two-dimensional geometric shape is the length of its outline or boundary. Depending on the dimensions, the perimeters of different figures can be equal in size. Consider a triangle made of a wire that is 12 cm long. If all the sides are the same length, the same wire can be used to create a square.

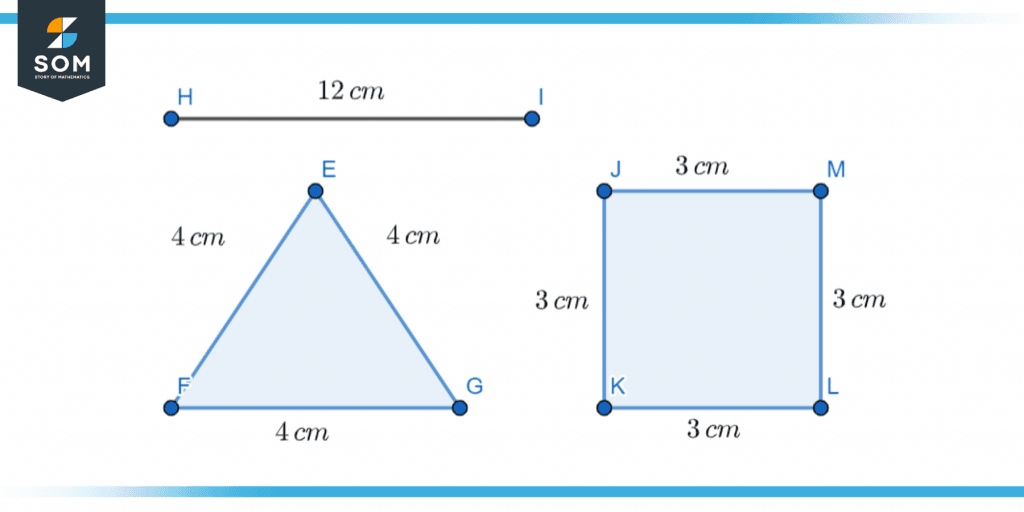
Figure 3 – Boundary of shapes.

Now that we know the perimeter of a geometric shape refers to its outer boundary, how would one determine its value? Let us look at an example. To prevent his cattle from straying off the farm, Jake wants to erect a fence around it. He is curious about the amount of wire required to fence his farm. His farm has a rectangular shape, which means:

• The farm has four sides.
• The length of the opposing sides is equal.
• Each angle is 90 degrees.

Now to find out the perimeter of his farm, Jack only needs to measure all four sides and add them together to get the perimeter of his farm.

Units of a Perimeter

The length that the shape’s perimeter covers are known as the perimeter. Therefore, the perimeter’s units will be the same as its length units. Perimeter is one-dimensional, as we can say. As a result, it can be measured in meters, kilometers, centimeters, etc. Inches, feet, yards, and miles are some additional perimeter measurement units that are recognized on a global scale.

The Formula of a Perimeter

The formula for calculating a perimeter changes according to our provided shape. The general formula for calculating a perimeter is as follows:

Perimeter = Sum of all borders

However, different formulas exist for various shapes. Below we can look at some of the commonly used formulas to calculate a perimeter:

• Square: The perimeter of the square = 4 x L, where L is the length of one boundary
• Rectangle: The perimeter of the rectangle = 2 x (L + B), where L and B are the Length and Breath of the rectangle.
• Triangle: The perimeter of a triangle = l + m + n, where l, m, and n are the lengths of a triangle.
• Circle: The perimeter of a Circle = $2 \pi r$, where $\pi$ is a constant and r is the circle’s radius.

Area of a Shape

The area of a 2-dimensional figure is the amount of space it takes up. In other words, it refers to the number of unit squares covering the surface of a shape enclosed by a boundary. The length and width of a shape are used to calculate its area. The units used to measure length are unidimensional and include meters (m), centimeters (cm), inches (in), etc. 

However, a shape’s area can only be measured in two dimensions. It is measured in square units, for example, meters or (m²), square centimeters or (cm²), square inches or (in²), and so on. The majority of the objects or shapes have edges and corners. These edges’ length and width are considered when calculating the area of a specific shape.

Calculating the Area of a Rectangle

The area is the space inside the boundary of a shape. The following figure shows a rectangle with a length of 5cm and a width of 3 cm. This formula can calculate the area of the rectangle: Area of Rectangle = l x w, where l is the length of the rectangle and w is the width.

Figure 4 – Perimeter of a rectangle.

Using the formula given, we can find the area of the rectangle. The area calculated is 3 cm x 5 cm = 15 cm.

Calculating the Area of a Circle

The shape of a circle is curved. The amount of space within a circle’s boundary is known as its area. The formula: $\pi$r², where r is the circle’s radius, and $\pi$ is a mathematical constant with a value roughly 3.14 or 22/7, is used to determine the area of a circle.

Looking at the figure below, we can see that the circle’s radius is 10cm.

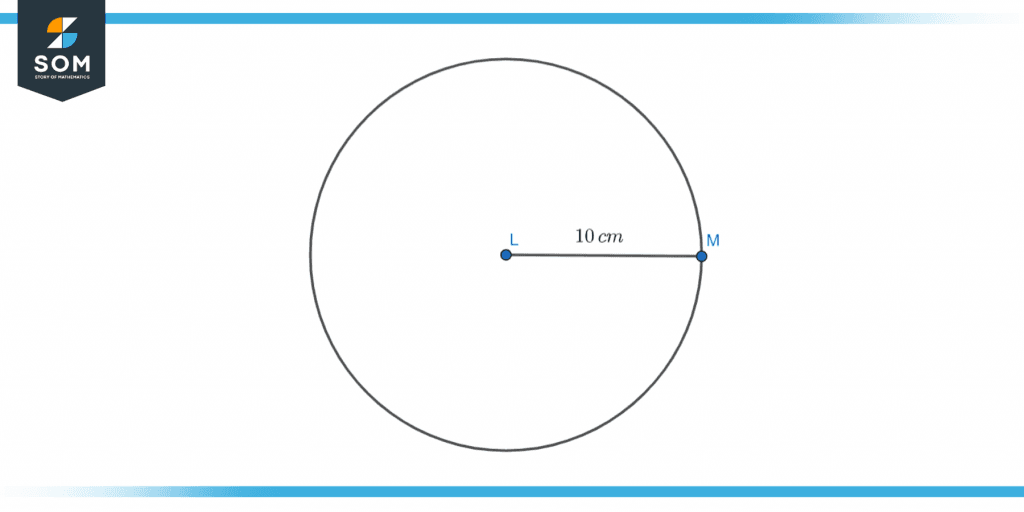
Figure 6 – Radius of a circle.

We can use the formula above to find the area of the circle. The area is calculated as shown below:

Area of Circle = $\pi$r²

Area of Circle = $\pi$ x (10 cm)²

Area of Circle = 100 x $\pi$ cm² $\approx$ 314.16 cm²

Example of Boundary

The following example on boundaries will help you understand the concept more easily.

In the following figures, distinguish the rectangular shape and find its perimeter. 

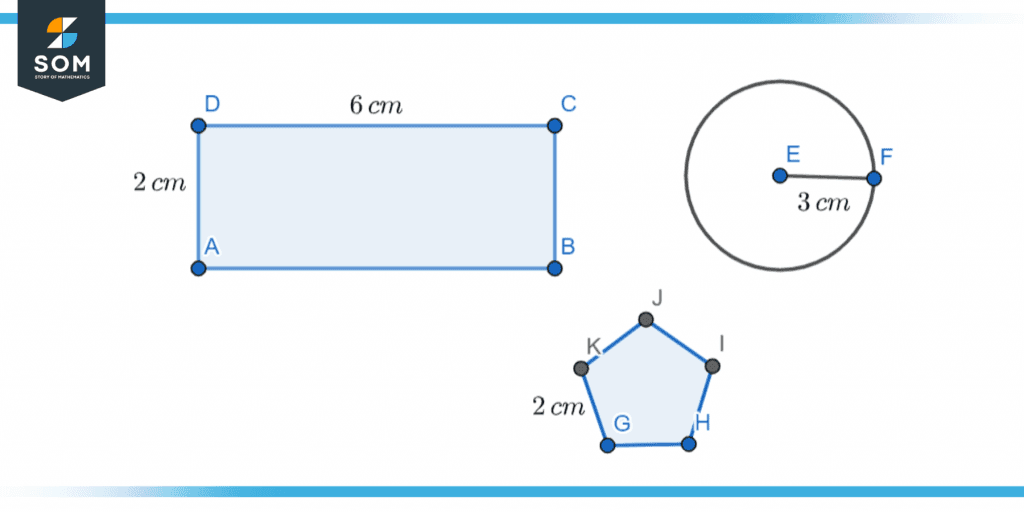
Figure 6 – Representation of boundaries.

Solution

We must find the rectangle from the given shapes in the first step. After closer inspection of the shapes, we can conclude that the shape ABCD is a rectangle. Now to calculate the perimeter of the rectangle, we use the following formula:

Perimeter of rectangle = 2(l x w)

Now we know the length of the rectangle is 6cm and the width is 2cm, we put these values in the formula.

Perimeter of rectangle = 2(6 cm + 2 cm)

After solving this formula, we get 18 cm².

All images/tables are created using GeoGebra.

Bivariate Data Definition < Glossary Index > Bounds Definition