Cancel|Definition & Meaning

When we talk about the cancel operation or the process of cancellation from the perspective of mathematics, we can’t really find much material for its proper formal introduction. This article will shed light on this important process in line with textbook methods. We will see how this process is important and how it may appear in different roles and different types of problems.

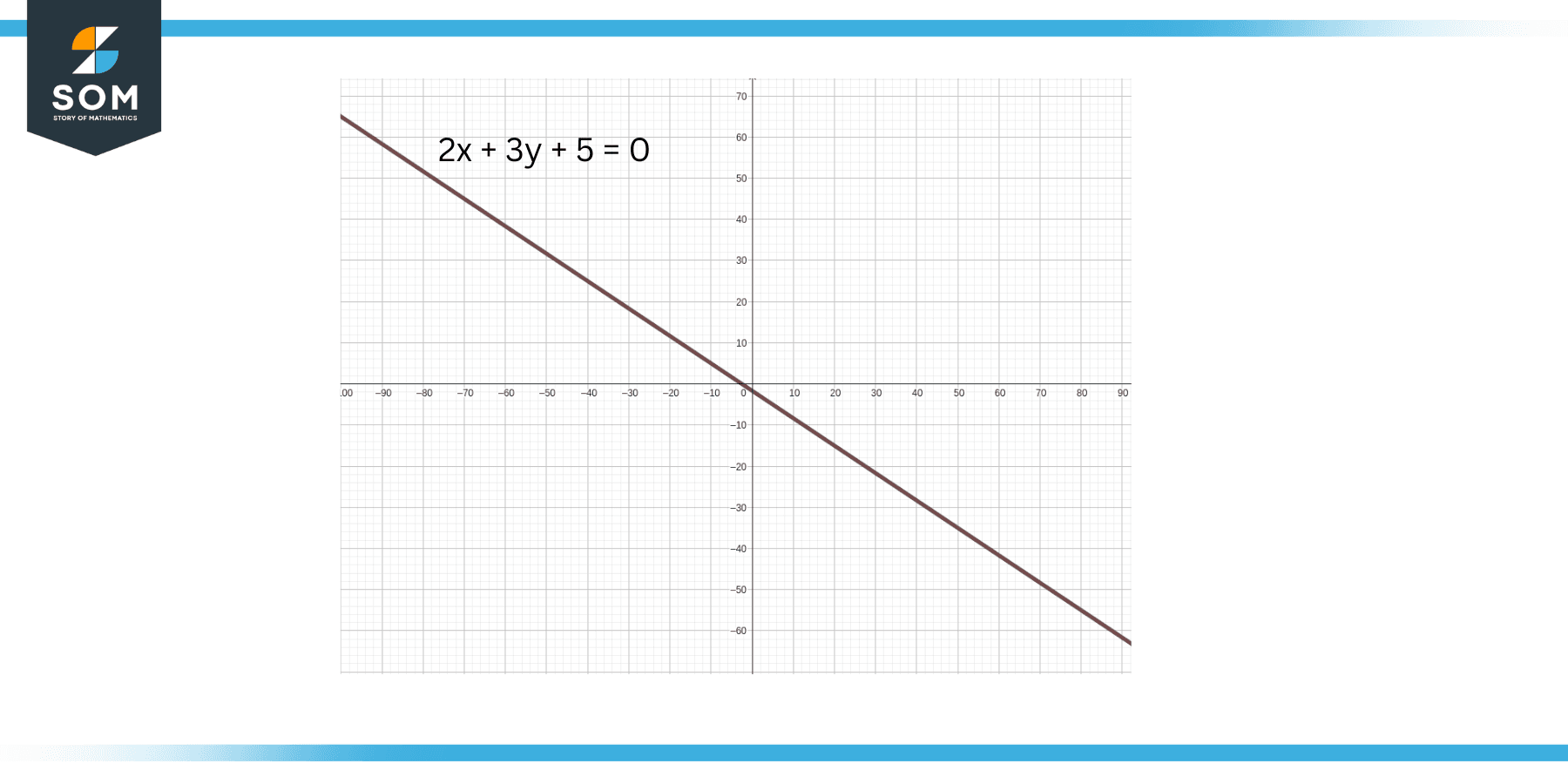
Figure 1: Graph of the Line 2x + 3y + 5 = 0 

The simplest process of cancellation may be based on addition or subtraction operations. However the operation is not limited to these arithmetic phenomena only. Rather the cancellation process may be applied to any other complex or implicit function as long as the inverse operator is defined.

In the following paragraphs, we explain the concept in more detail.

Examples of Cancellation Process

There is a special type of cancellation process called the anomalous cancellation. Anomalous cancellation is such a process in which given a fraction of the form p/q, we may write it in the form of ac/bd such that a = b which further reduces the expression to c/d. Now c/d is a simpler expression that may look different yet the mathematical meaning remains the same.

For example, consider the case of following fraction:

30/70

This expression may be written as:

30/70 = (3/10) / (7/10) = 3/7

Now, the fraction 3/7 is a much simpler expression, but it has the same meaning in terms of mathematics.

Visual Intuition of Cancel Operation

To understand the cancel operation we need to consider an example. Let us say that you have an equation of a line defined as follows:

2x + 3y + 5 = 0

Keep in mind that it is derived from the standard line equation ( ax + by + c = 0 ). The figure 1 plots this line in a 2D XY plane. Now let us multiply this equation with a scalar, say 10, for example, and see how the line is affected. The above equation will change as follows:

10 (2x + 3y + 5) = 10(0)

20x + 30y + 50 = 0

Following figure plots this new line in 2D XY plane:

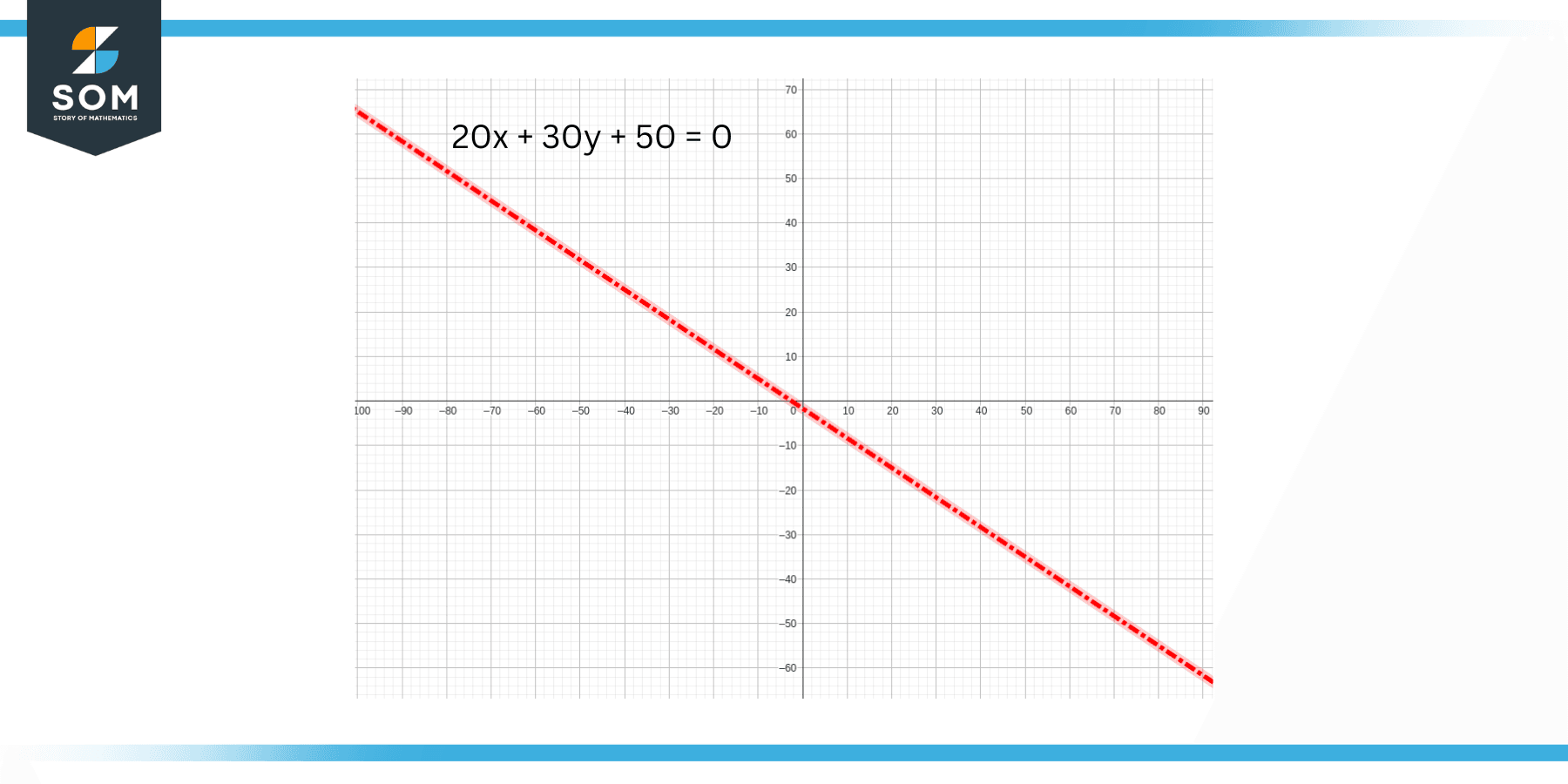
Figure 2: Graph of the Line 20x + 30y + 50 = 0

If you compare figures 1 and 2, you can clearly see that there is no difference in the actual line and its graph. Both equations represent the same line in the physical world. This means that the factor we multiplied with the original equation had no effect on the mathematical meaning of the equation or expression.

If we converse the statement, we can conclude that starting from the polynomial 20x + 30y + 50 = 0, we can find a factor that is common on the left-hand side, and it can be canceled out without any change in the mathematical meaning of the expression.

Consider another example of a parabola. Suppose you are given the following equation of a parabola:

y  + 10x + 7 = x² + 8x + 4

The following figure plots this equation in the 2D plane:

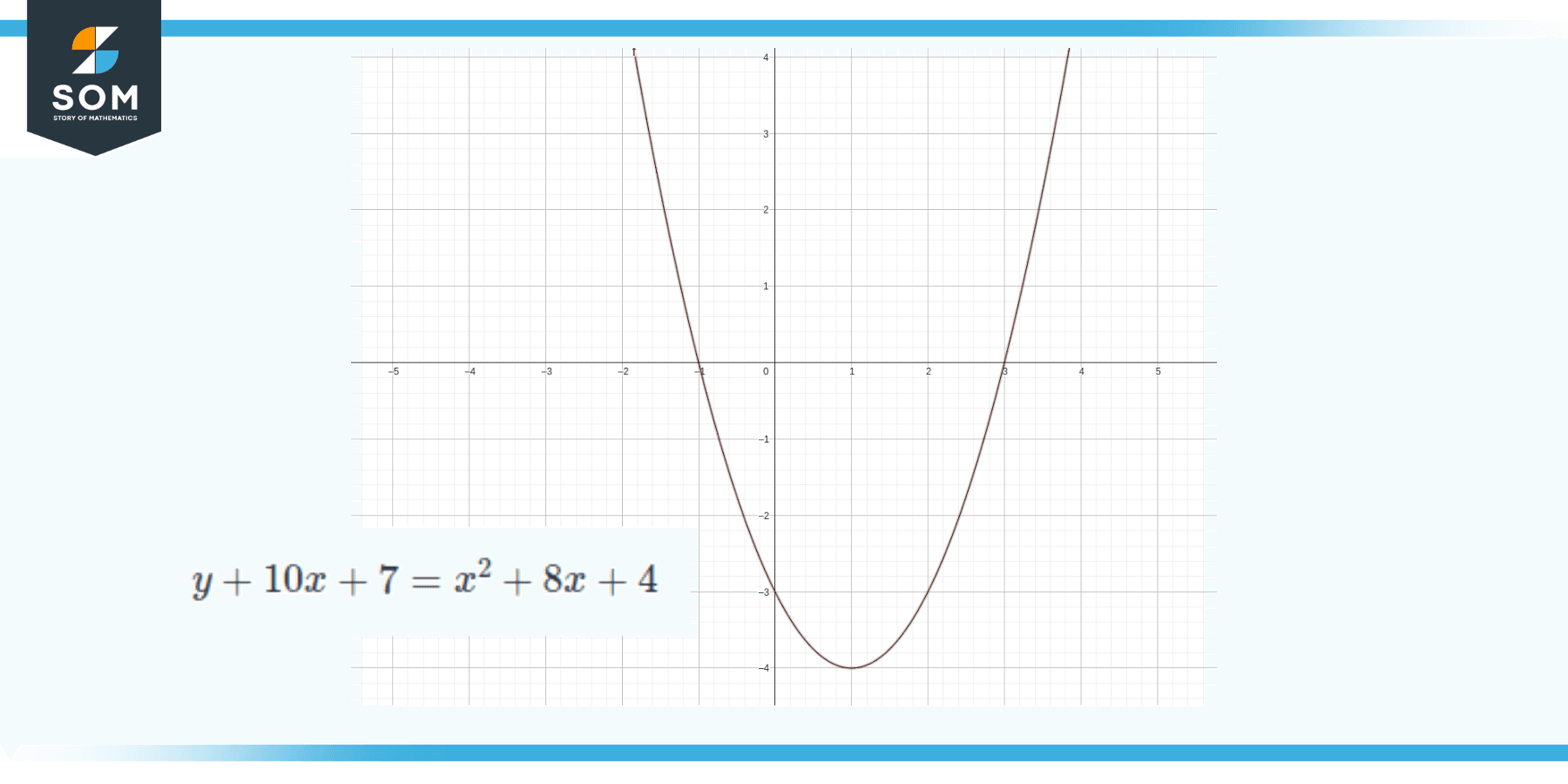
Figure 3: Graph of the Parabola y + 10x + 7 = x² + 8x + 4

Now at first glance, the equation looks nothing like a parabola and seems quite complex. If you look closely, it can be seen that the two of three expressions on the left hand side can be canceled out from the right hand side if we just split the right hand side like so:

y  + (2x + 8x) + (3 + 4) = x² + 8x + 4

y  + 2x + 8x + 3 + 4 = x² + 8x + 4

Now it is very clear that the terms 8x and 4 are on both sides of the equation and can be canceled out, which reduces the equation to the following:

y  + 2x + 3 = x²

Rearranging the equation yields:

y  = x² – 2x – 3

Which is a quadratic equation that looks much more simpler and similar to a parabola equation. The following figure plots the above expression along with the expression plotted in figure 3.

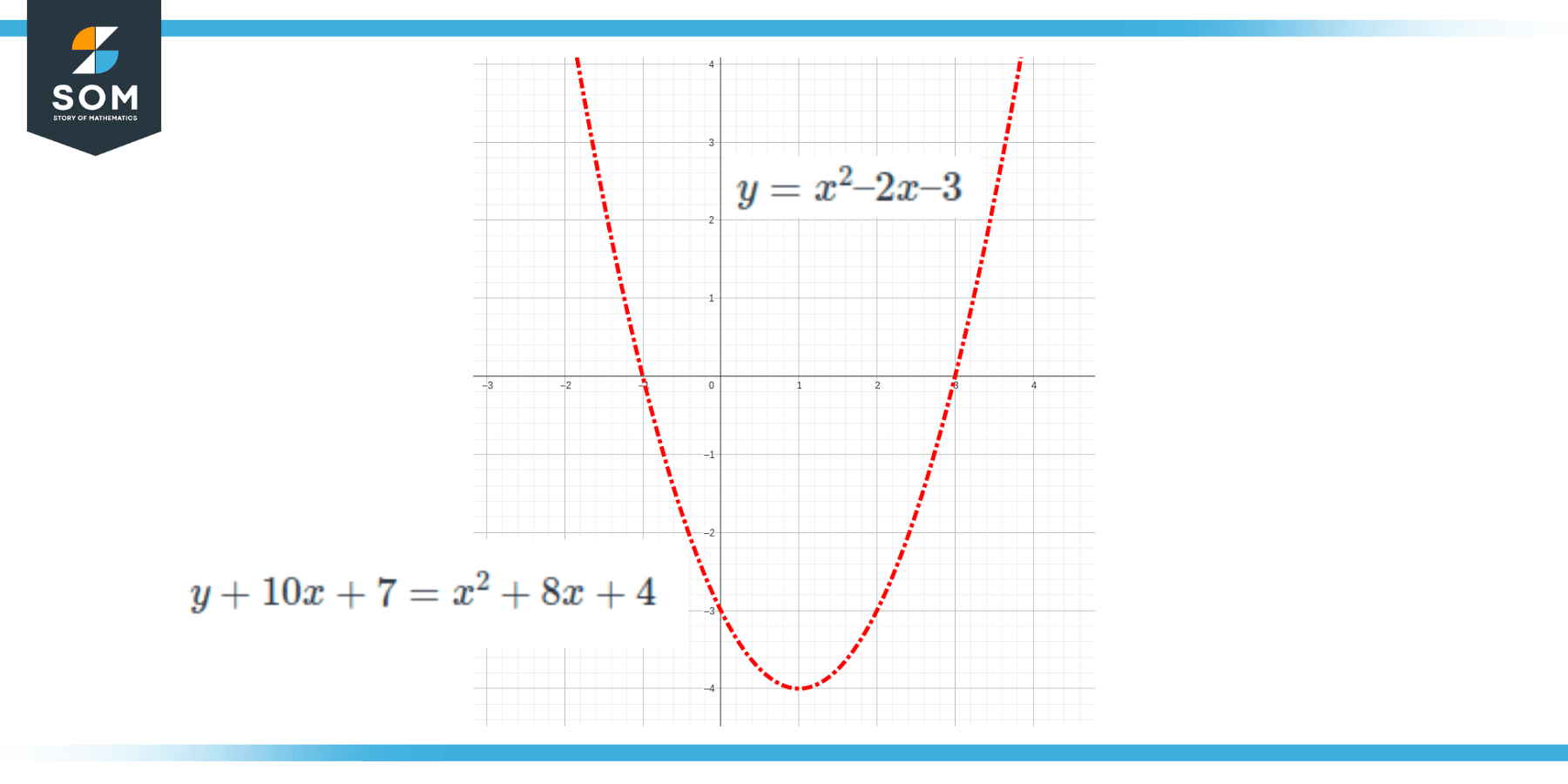
Figure 4: Graph of the Parabola y = x² – 2x – 3

It is clear the the simpler expression of figure 4 and the more complex form of figure 3 are mathematically the same. These examples clarify the meaning and significance of the cancellation process. There are also quite a few simpler examples that we will solve in the following section of the article.

Numerical Problems of Cancelation

Simplify the following expressions using the cancellation or anomalous cancellation:

(a) y + 15 x = 10 x + 5

(b) 144/108

(c) (55 * y) / 10  + 2 x = 55 / 10

Solution

Part (a) – Given that:

y + 15x = 10x + 5

Splitting 15x into two terms as the sum of 10x and 5x:

y + 10x + 5x = 10x + 5

Canceling out the 10x term on both sides:

y + 5x = 5

which is the simplest expression.

Part (b) – We are given that:

144/108

Factorizing both the denominator and the numerator, we end up with the following:

(12)(12) / (12)(9)

Canceling out the factor 12 as it exists in both numerator and denominator:

 12 / 9

Further factorizing the fraction, we get:

(4)(3) / (3)(3)

Canceling out the factor of 3 in the numerator and denominator:

4 / 3

which is the simplest expression.

Part (c) – We have the expression:

(55 * y) / 10  + 2 x = 55 / 10

Factorizing both the denominator and the numerator on both sides:

(11)(5)(y) / (2)(5) + 2 x = (11)(5) / (2)(5)

Canceling out the factor of 5 as it exists in both the numerator and denominator:

(11 * y) / 2 + 2 x = 11 / 2

which is the simplest expression.

All mathematical drawings and images were created with GeoGebra.

Byte Definition < Glossary Index > Capacity Definition