Capacity|Definition & Meaning

Air or liquid is filled within hollow objects, giving the containers their shape. In a container, its capacity is determined by the amount of air and water accumulated inside. Although there are many similarities between volume and capacity, we can still distinguish between them. The capacity of a container refers to the amount of solid, liquid, or gas it can contain, as well as its weight.  

Illustration of Capacity

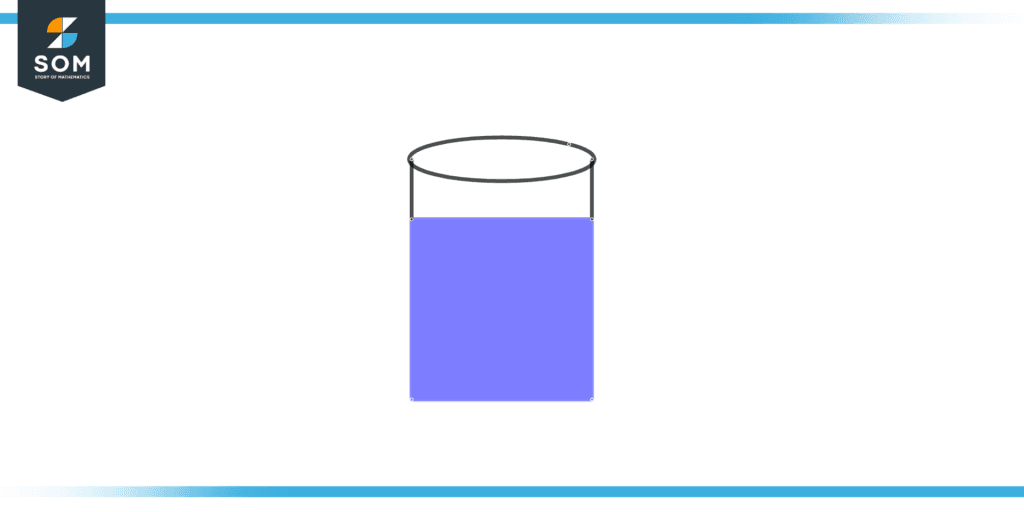
Figure 1 – Capacity of a Jar

Above, we can see that the jar is partially filled with water. The capacity of the jar indicates the amount of water it can hold. Alternatively, the formula of the volume of a jar /cylinder can be used to find the jar’s capacity.

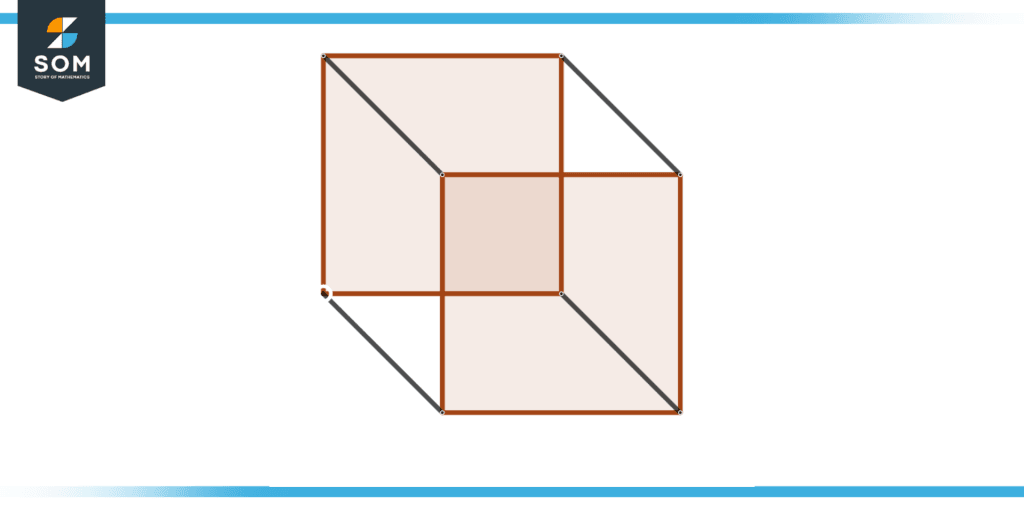
Figure 2 – Capacity of Water Tub

In the figure shown above, we can see a square water tub whose capacity might be around 4 to 5 liters.

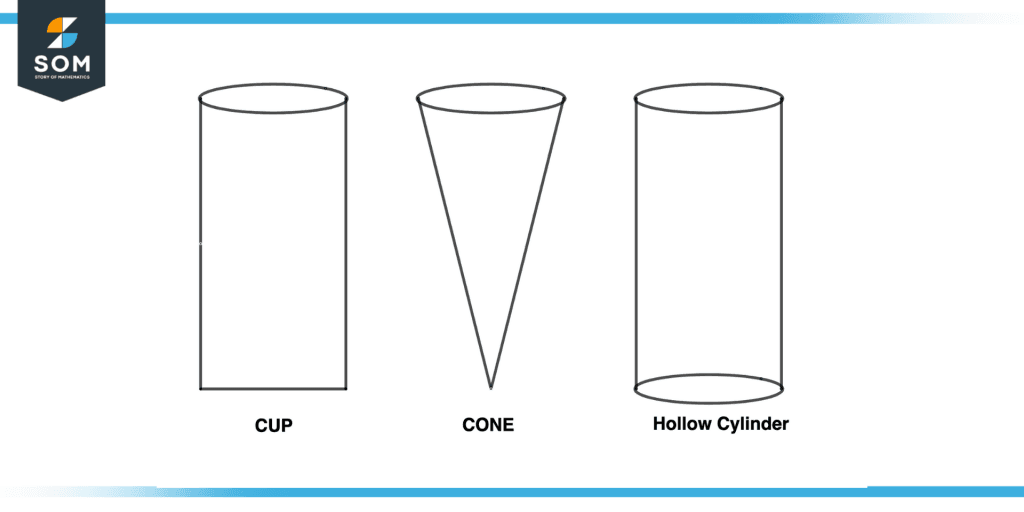
Figure 3 – Objects Having Capacity

The above figure shows the various objects having capacity, in the cup, there is generally a capacity of 250mL to 500ml, the capacity of a cone varies from application to application but its generally around 30mL and the capacity of the cylinder can also be calculated by the dimensions of the cylinder, it usually ranges around 5L.

Units of Capacity

The standard unit for capacity is Litre or milliliter but other than that also various units for capacity used in daily life include gallon, quart, and a pint. We will discuss them one by one.

Litre

The liter is a metric measurement unit that measures volume and capacity. Containers are measured by their capacity, not their volumes. Volume denotes how much space a liquid occupies, while capacity indicates how much liquid can be contained.

Milliliter

Using milliliters as measurements of liquid capacity, the metric system has been simplified. Liquids of a smaller volume or capacity, such as pharmaceutical solutions, are measured with this unit. In metric systems, milliliters are abbreviated mL. 

Gallon

U.S. customary and imperial systems of measurement define the gallon as a unit of volume and capacity. 

Pint

It is also a unit of capacity and it is equal to around 0.47 liter.

Quart

It is equal to ¼ of a gallon or two pints or 0.94 liter

Conversion Between Units

1 Litre = 1000ml

1 mL = 1/1000L

1 Gallon = 3.785L

1 pint = 0.473L

1 Quart = 0.94L

Capacity and Volume Comparison

There are several differences between capacity and volume that make the two terms different, but usually, they are treated as the same. Volume refers to the area of a particular space containing a total amount of any substance contained within it. An area’s capacity refers to its ability to contain all of the substances that it can hold.

For volume, we have the following facts:

• Objects in three dimensions are measured by their volume, which represents their coverage of space.
• The unit to express volume is a meter cube or centimeter cube.
• The objects that have volume are usually in form of solids like ice, and hollow like hollow cones.

Whereas, for capacity, we have:

• Objects are capable of holding, absorbing, or receiving something that has the capacity (such as solids, gases, or liquids).
• Units to express capacity include Litre, milliliter, gallon, pint, quart, etc.
• Only hollow objects have capacity like cones and cylinders.

Thus, the two terms mean different things, although they are closely related.

Examples of Calculating Capacities

Example 1

Consider a cube water tub and the capacity of the object is 1.75 Litres convert the capacity into (a) milliliter (b) Gallon (c) Pint (d) Quart.

Solution

(a) Litre to mL:

1 Litre = 1000ml

1.75 Litre = 1000 x 1.75 Litre

1.75 Litre = 1750mL

(b) Litre to Gallon (US):

3.785 L = 1 Gallon

1 Litre = 0.2641 Gallon

1.75 Litre = 0.2641 x 1.75 Litre

1.75 Litre = 0.462175 Gallon

(c) Litre to Pint

0.473L = 1 pint

1 Litre = 2.113 pint

1.75 Litre = 2.113 pint x 1.75 Litre

1.75 Litre = 3.698 pint

(d) Litre to Quart

0.956L = 1 Quart

1 Litre = 1.056 Quart

1.75 Litre = 1.75 Litre x 1.056 Quart

1.75 Litre = 1.849 Quart

Example 2

Consider the two aquariums labeled aquarium 1 and aquarium 2. There is a bucket of capacity having 1 Litre. How will you measure the capacity of aquarium 1 and aquarium 2 from the bucket? Explain the hypothetical procedure.

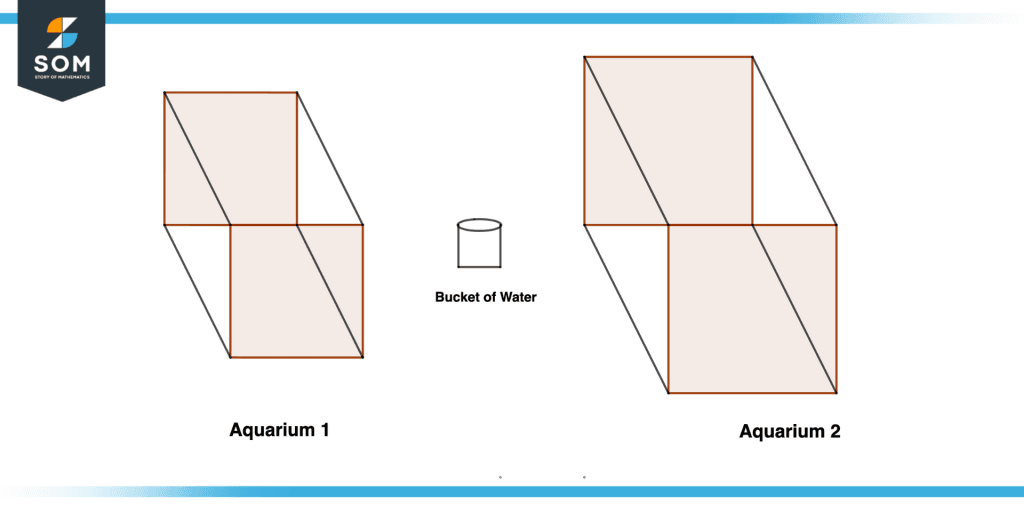
Figure 4 – Capacity of Aquarium

Solution

First, let us find the capacity of Aquarium 1.

We are given a bucket having a 1 litre capacity so we will do a small activity. First, we will fill the bucket with water and pour the bucket until the aquarium is full. So when we kept on pouring the water from the bucket into the aquarium we came to know that it takes 5 buckets to fill the whole aquarium 1 so mathematically.

1 bucket = 1 litre

No of bucket poured to fill the aquarium 1 to full = 5 = Capacity of Aquarium

Capacity of Aquarium 1 = 5 buckets x 1 litre

Capacity of Aquarium 1 = 5 Litres

Now, let us find the capacity of Aquarium 2.

On repeating the above methodology or when we kept on pouring the water from the bucket into aquarium 2 we came to know that it takes 10 buckets to fill the whole aquarium 2 so mathematically.

1 bucket = 1 litre

No of buckets poured to fill the aquarium 2 to full = 10 = Capacity of Aquarium

Capacity of Aquarium 2 = 10 buckets x 1 litre

The capacity of Aquarium 2 = 10 Litres

Example 3

Consider a Flask and spoon. The capacity of the spoon is 10mL and we want to find the capacity of the Flask. Explain the hypothetical procedure.

Figure 5 – Capacity of Flask

Solution

We have a spoon of 10mL and a flask with an unknown capacity so what we will do is we will keep on adding liquid in a 10mL spoon and pour it into the flask, we will continue to perform the activity unless the flask reaches a full quantity. Let’s suppose we put 20 spoons full of liquid into the flask so that it reached its full quantity so mathematically.

1 spoon = 10mL

No of spoon poured to fill the flask = 20

The capacity of the flask = capacity of spoon * no of spoon poured to fill the flask

Capacity of flask = 10ml x 20

Capacity of flask = 200ml

All mathematical drawings and images were created with GeoGebra.

Cancel Definition < Glossary Index > Cartesian Coordinates Definition