JUMP TO TOPIC
Cartesian Coordinates|Definition & Meaning
Definition
The cartesian coordinate system is a system which determine the location of any point in a plane. It could be two dimensional or three dimensional through two coordinate which are x-coordinate and y-coordinate.
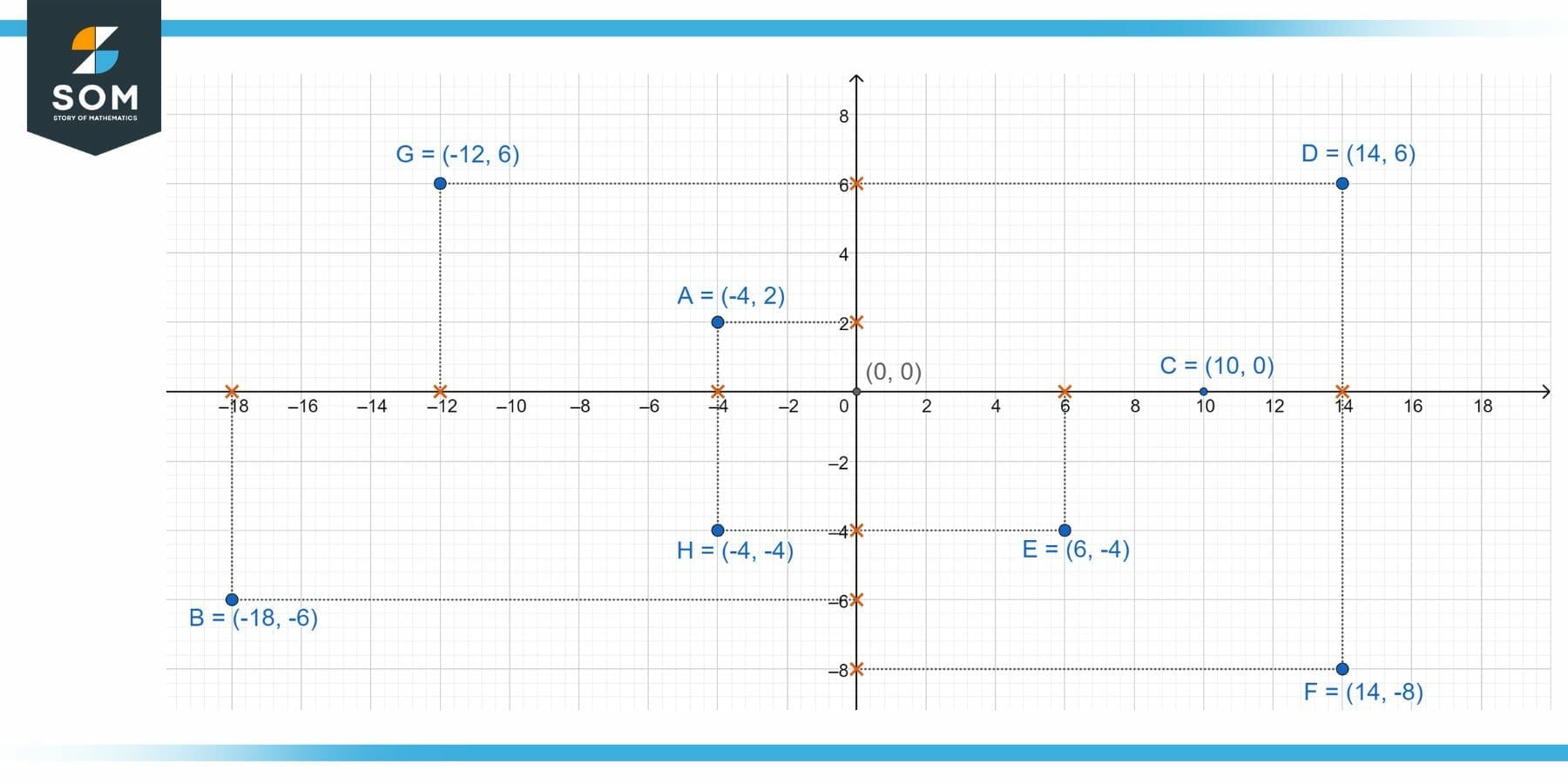
Figure 1 – Various points on a Cartesian plane. Each point has some Cartesian coordinates.
Cartesian Coordinate System
A branch of mathematics known as cartesian coordinate system describes how to represent a point in the n-dimensional coordinate plane in a singular way. The Cartesian coordinate system is indeed not complicated or complex; it was not invented after years of study or thought.
In the 17th century, Rene Descartes, a French mathematician and philosopher , proposed the notion of the cartesian system. Descartes came up with it while resting in his bed and noticing a fly flying around. He attempted to figure out the precise position of the fly by imagining his ceiling as a square and describing the exact location of the fly by estimating the distance that needed to be traversed in the horizontal and vertical directions.
Explanation
The link with algebra and Euclidean geometry and was given by the cartesian coordinate system, which transformed the field of mathematics. The basis of analytical geometry is the cartesian coordinate system, which aids in the depiction of lines, curves, and geometric forms in the n-dimensional plane. Let’s find out more about the terminologies used in the cartesian system.
One can indicate the position of a particular point in the plane or in three dimensions using cartesian coordinates. A pair of integers (in two dimensions) or even a triplet of numbers (in three dimensions) specifying indicated distances from the coordinate axis are known as a point’s Cartesian coordinates, also known as rectangular coordinates.
Cartesian Coordinate and Real Life
Students’ most frequently asked questions throughout Math class are, “Will I ever apply it in my daily life?” Why would we need to understand and how to determine the position of a particular point on a planar surface? The solution is straightforward.
Coordinate systems may be the most often utilized mathematic technique that we learn in school and see or use almost every day. It exists all around us; it is so ingrained in our lives that we no longer perceive it. When we offer someone driving directions, we tell them to go to the right and then to the left; this is exactly what the coordinate system is.
Cartesian coordinates are also vital tools in most applied geometry disciplines, such as astronomy, physics, engineering, and many more. They are the most often used coordinate system in computer-aided geometric design, computer graphics, and other data processing involving geometry.
Examples of Cartesian Coordinates in Plane and Space
Example 1
Plot the cartesian coordinates (-3, 2) and (2, 3) on a 2D graph. Where is the origin? How does the sign of the coordinate affect its placement relative to the origin?
Solution
There are two points shown in the figure below. The first point is A which has coordinates (-3,2) which is locating the point with respect to x and y axis. Here x coordinate is -3 negative sign is showing the left side of x axis from the origin and 3 is representing the magnitude with respect to origin. Like wise 2 is representing y coordinate of the point that is the point is 2 points away in the upper direction from the origin. Same concept goes for point B, here (2,3) are the coordinates of the point and is locating the point in the plane. The point B is at the 2 magnitude and 3 magnitude away from the x and y axis respectively.
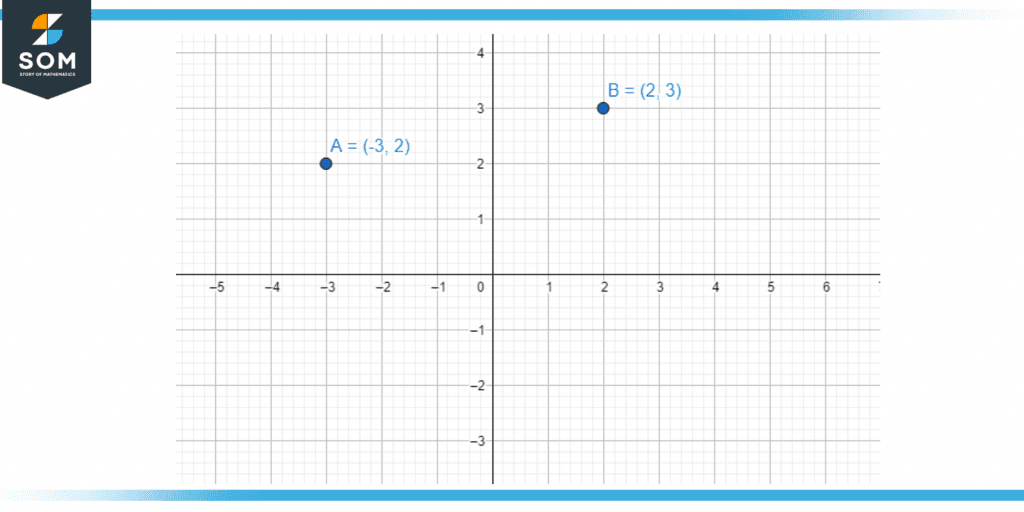
Figure 2 – Points A and B on the two Dimensional plane.
According to the illustration in the figure above, the x and y coordinate axes are used to specify the Cartesian coordinates in the plane. The x and y axes junction serves as the origin, and (x,y) represents a point’s Cartesian coordinates in the plane.
The first integer x, which represents the distance from the origin in the direction of the x-axis, is known as the x-coordinate (or x-component). If x is positive or negative, the x-coordinate indicates how far the y-axis is to the right or left, respectively. The second value y is referred to as the y-coordinate (or y-component) since it represents the signed distance from the origin along the y-axis.
Example 2
Plot the points (-25, -15), (0, 0), and (20, 10) on the Cartesian plane.
Solution
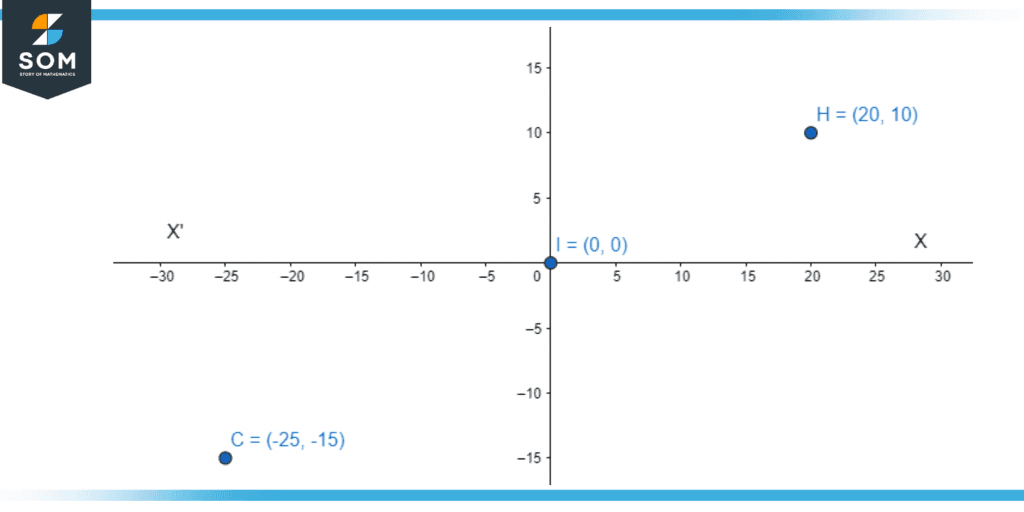
Figure 3 – Cartesian Coordinates on the two-dimensional plane.
The above figure is representing three points on the 2-Dimentional Cartesian Plane. Point I has coordinates (0,0) which means it is at origin, the next point H has coordinates (20,10) which means this point is at the magnitude of 20 and 10 with respect to x and y axis respectively. The third and the last point is C with coordinates (-25,-15) the negative sign sowing the direction of the coordinates and the digits are the magnitude with respect to origin.
We have not talked about them, but these points satisfy a property called collinearity. That is, a single line can pass through all of these points.
Further, the distance between the two points (x1, y1) and (x2, y2) is equivalent to the under root of the sum of the squared values of the difference between their respective x and y coordinates. The following is a formula for calculating the separation between two points, called the distance formula:
\[ \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \]
Example 3
Plot the points (3, 7), (8, 8), and (4, 12) along the axes X, Y, and Z axes respectively.
Solution
The x, y, and z axes, which are all perpendicular to one another and share the same units of length on all three axes, make up the three-dimensional cartesian coordinate system. Similarly, like a two-dimensional coordinate system, these three axes intersect at origin O, dividing the space into eight units called octants.
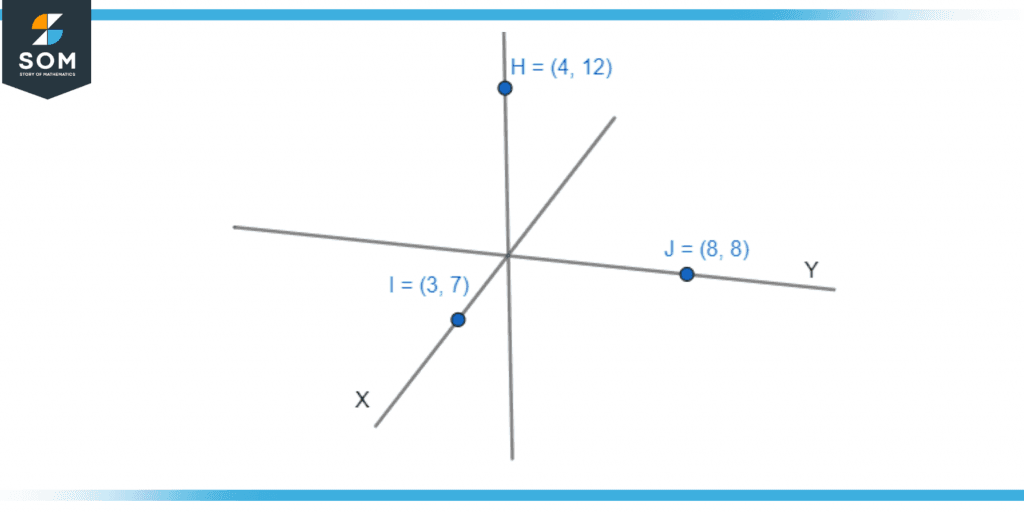
Figure 4 – Cartesian Coordinates in three-dimensional space.
Keep in mind that the cartesian coordinate system can represent several quantities simultaneously using an n-dimensional system. However, the greater dimensions cannot be assumed and shown geometrically. Major uses for the high dimension systems can be found in artificial intelligence and computer programming.
All mathematical drawings and images were created with GeoGebra.
