JUMP TO TOPIC
Center|Definition & Meaning
Definition
A center is generally a point at the center of an object in geometry. Centers may or may not exist depending on the definition of the term taken into consideration. The center is defined as the point where all the isometries that move the object onto itself have a fixed point if we consider geometry as the study of isometry groups.
Circles, spheres, triangles, and line segments have many points inside them, and each point is situated at a different distance from the other points. The center of a geometric object (circle, triangle, line segment) however, is comprised of only one point, which is always the same distance from every other point.
Center of Circle
Circle centers correspond to the points on a circle that are equal distances from one another in other words circle centers are points that are equally distant from their edges.
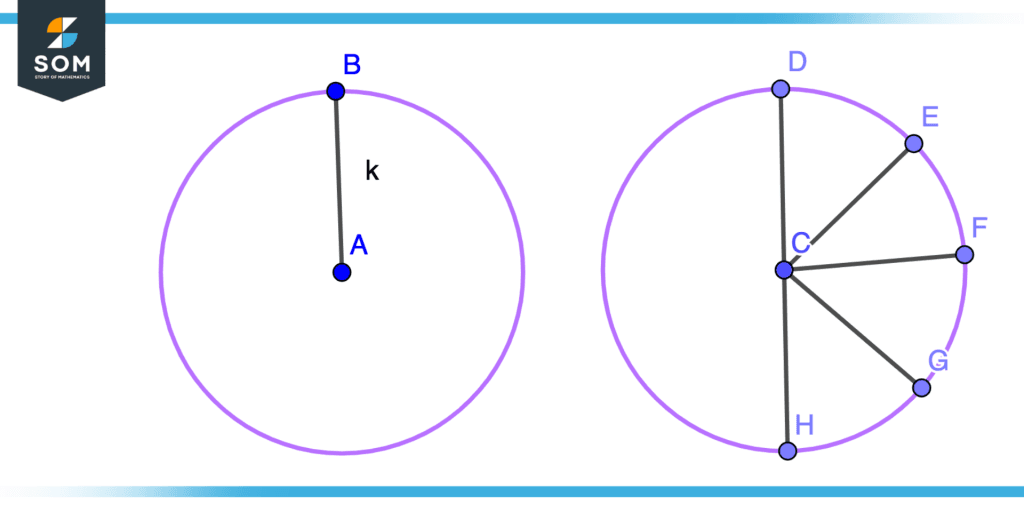
Figure 1 – Center of Circle
Consider the figure above where a circle is drawn the point A is labeled as the center of the circle where AB is the radius with B as a point on the circle. The reason we are calling A the center of the circle is that the distance of all the points in the circle from point A(center) is equidistant.
Consider the right circle in above figure C is labeled as the Center of the circle while D, E, F, G, and H are points on the circle so all of these points will be equidistant that’s what we define above the definition of a circle and referring C as the center of the circle.
CD = CE = CF = CG = CH
The formula for finding the center of circles can be expressed by the general equation for the circle. In a circle, consider (L, M), r, and (X, Y) as the coordinates of the center of the circle, the radius of the circle, and the coordinates of any point on the circle respectively. The center formula of the circle can be written as :
(X – L)² + (Y – M)² =r²
Center of Sphere
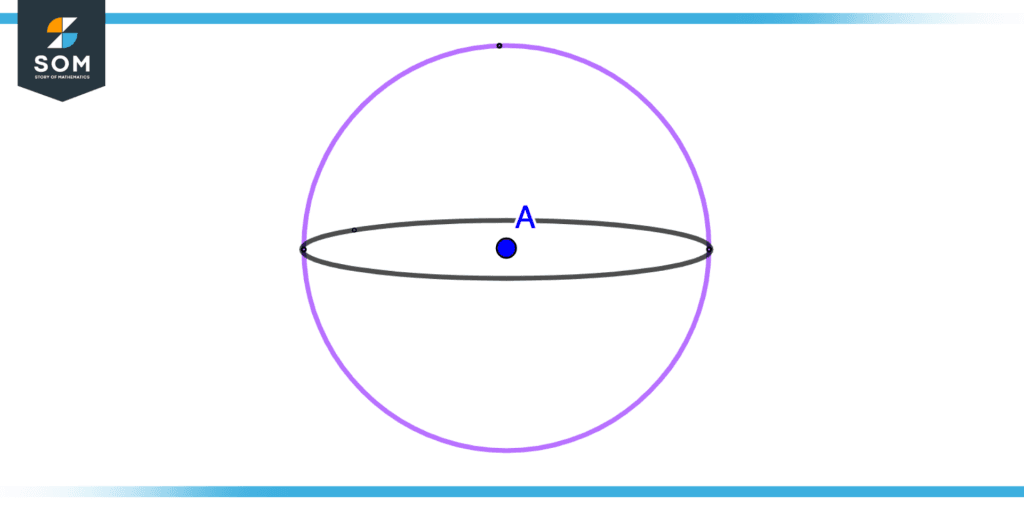
Figure 2 – Center of Sphere
Spheres are three-dimensional space objects formed by points that are equally distant from a point and that point is known as the center of the sphere.
Consider the above figure point A is known as the center of the sphere because that point is equidistant from all the points on the surface of a sphere.
The formula for finding the sphere can be expressed by the general equation for the sphere. In a sphere, consider (L, M, N), r, and (X, Y, Z) as the coordinates of the center of the sphere, the radius of the sphere, and the coordinates of any point on the sphere respectively. The center formula of the sphere can be written as :
(X – L)² + (Y – M)² + (Z – N)² =r²
Center of Triangle
An actual triangle center or triangle center in geometry is a point on a plane that, in some sense, is in the middle of the triangle, similar to the center of a square or circle. There are many distinct points of triangles that are referred to as the center of the triangle as described below. Consider the below figure of an equilateral triangle the center is labeled as H where all three vertices of the triangle pass.
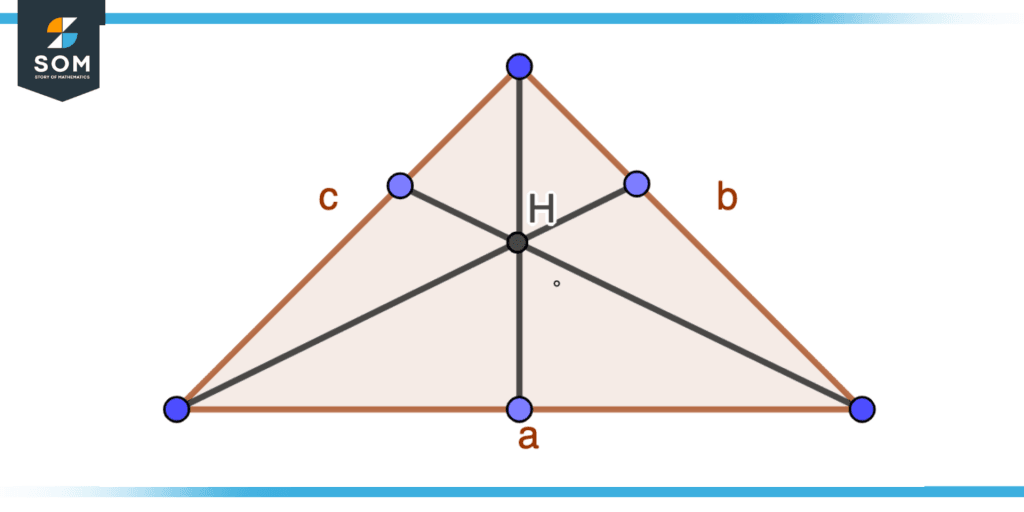
Figure 3 – Center of Triangle
Circumcenter
Consider three vertices of the triangle, the center of the triangle will be the point that passes through all three vertices.
Centroid
Consider a triangle that has a uniform density so the centroid will be the point where the triangle is balanced.
Incentre
Consider a triangle the incentre can be defined as the point where the internal angle bisector meets or the center that is tangent to the three sides of the triangle.
Orthocenter
Consider a triangle the orthocenter can be defined as the point where the altitudes of the triangle intersect.
Center of Polygon
Given a regular polygon, the center of the polygon can be defined as a point (k) that is equidistant from all of the vertices as shown in the figure below.
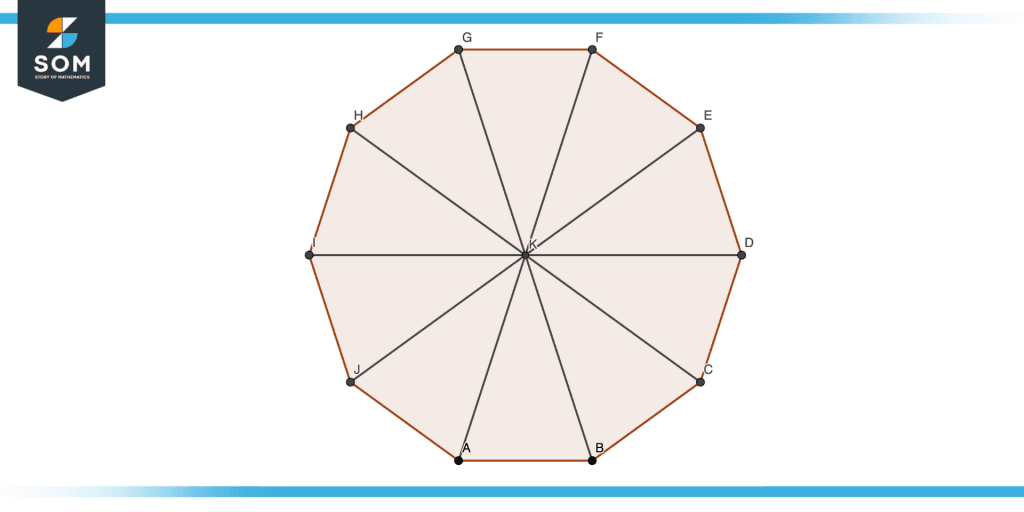
Figure 4 – Center of Polygon
There are other types of polygons like cyclic and tangential polygons we will also discuss their center as well.
Center of Tangential Polygon
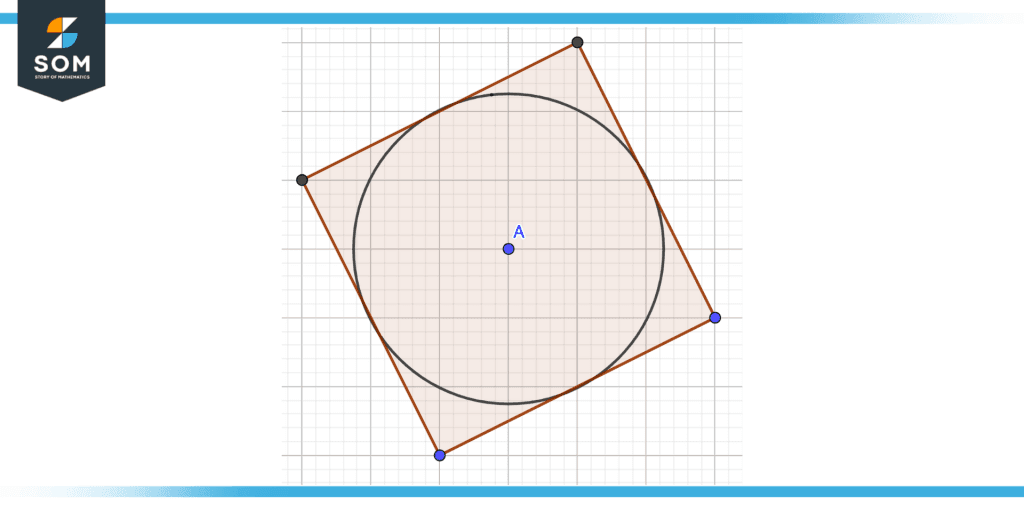
Figure 5 – Center of Tangential Polygon
Consider a tangential polygon that has all of its vertices tangent to a distinct circle that circle is known as an incircle (inscribed circle) and the center of that circle (incenter) is referred to as the center of the tangential polygon. The center of the tangential polygon is A.
Center of Cyclic Polygon
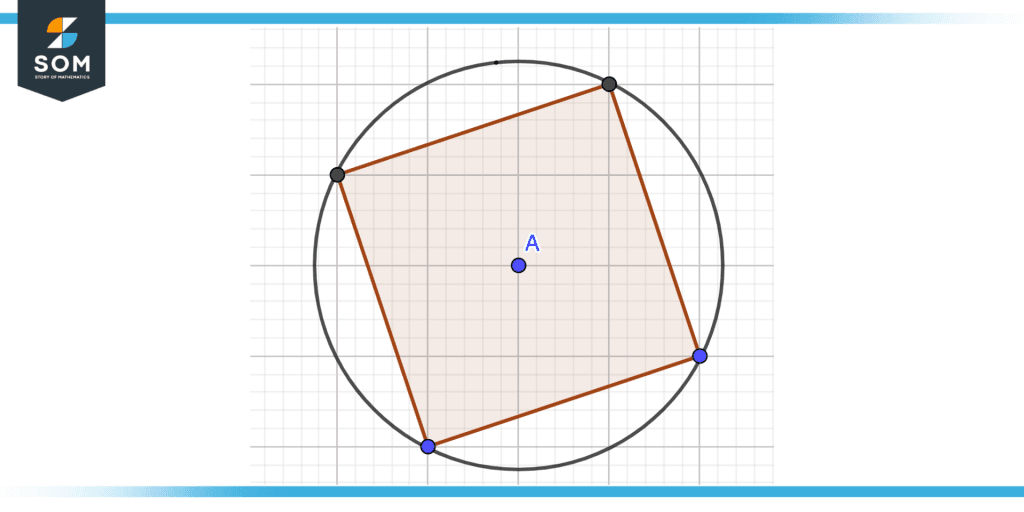
Figure 6 – Center of Cyclic Polygon
Consider a cyclic polygon that has all of its vertices on a distinct circle that circle is known as a circumcircle and the center of that circle (circumcenter) is known as the center of the cyclic polygon as shown in the figure. The center of the cyclic polygon is A.
Center of Line Segment
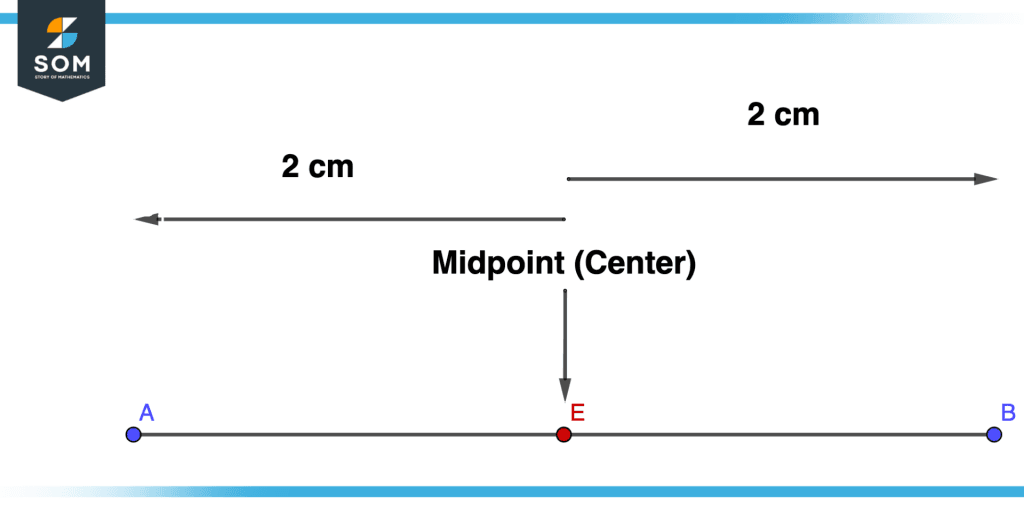
Figure 7 – Center of Line Segment
The Center of a line segment is usually referred to as the midpoint which is basically mid of two points. Let’s suppose two points A and B to find the midpoint we will calculate the distance between the two points and divide that distance into two parts.
For instance, there are two points and the distance between them is 4cm to find the center of the line segment i.e. the midpoint we will divide the distance by 2 and what we get is 2 so the midpoint (center) will on 2cm from A and 2cm from B. This concept is illustrated in the figure below. E is the midpoint of the line segment.
Locating Centers – An Example
Consider the following figure having two problems A and B the data is given in the figure we want to find the center of the circle and the center of the line segment.
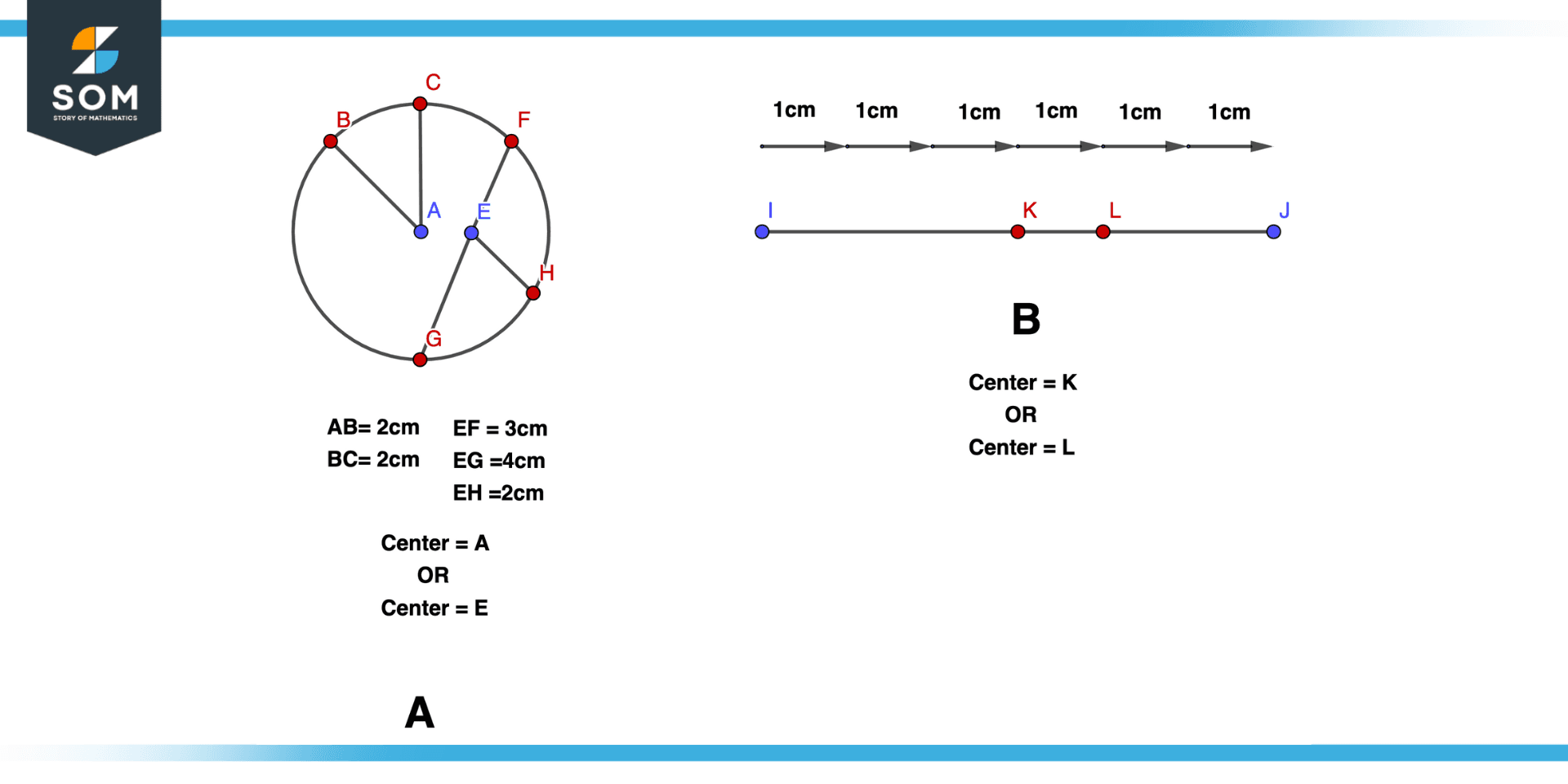
Figure 8 – Example of the Center of a Circle and Line Segment
Solution
First, let us solve for Figure A.
There are two points given A and E, according to the given data
AB=2cm
AC = 2cm
Both the points are equidistant while we are also given that:
EF = 3cm
EG = 2cm
EH = 4cm
Three of the given points are not equidistant, so E is not the circle’s center. Thus, we conclude that A is the center of the circle as it is equidistant from all points on the circle.
Moving on to Figure B, we have two points K and L.
To find the center, we will first find the distance between I and J which turns out to be 6cm. Dividing this distance by 2 gives us 3cm, so we will now look at the point that is 3cm away from I and J. In the case of L, it is 4 cm away from I and 2cm away from J while in the case of K, it is 3cm away from I and 3cm away from J so we will conclude K is the midpoint or center of the line segment.
All mathematical drawings and images were created with GeoGebra.
