Certain|Definition & Meaning

Figure 1 shows a certain event.

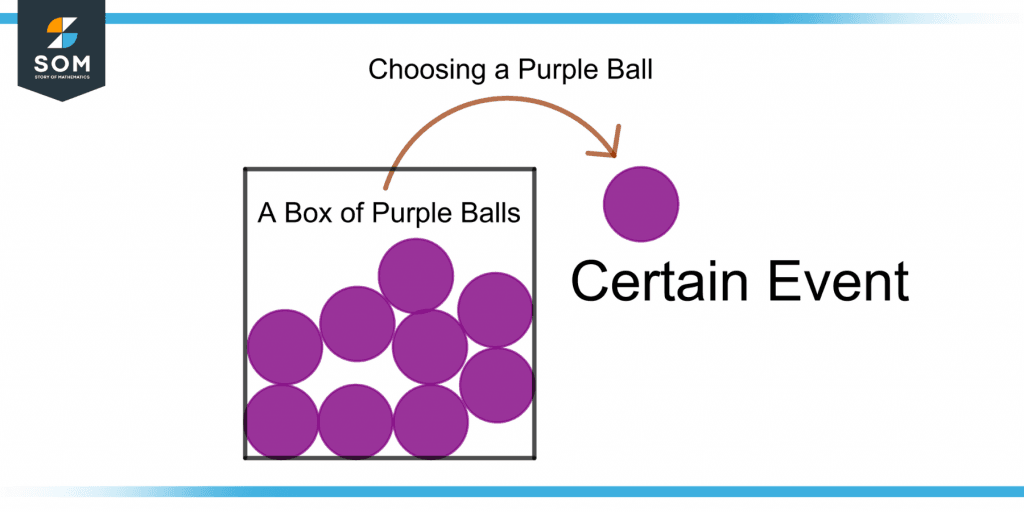
Figure 1 – An Example of a Certain Event

Choosing a purple ball from a box of purple balls is a certain or sure event. 

Probability

Probability is a numerical quantity that defines the degree of how much there is a likelihood of an event taking place.

The probability of a particular outcome is the ratio of the number of favorable outcomes to the total number of outcomes that can occur.

The mathematical formula for probability is given as:

Probability of an Event To Occur = P(E) = n(E) / n(S)

Where,

n(E) = Number of Ways the Event Can Occur

n(S) = Total Number of Events

Figure 2 shows the procedure to find probability.

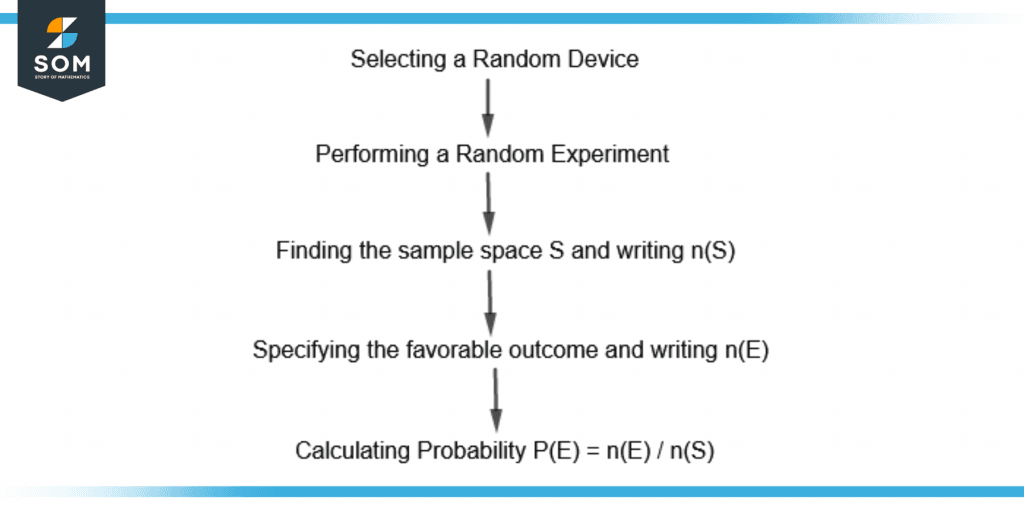
Figure 2 – Flowchart for Finding Probability

Random Device

In probability, random devices are used to produce random outcomes. The experiment can result in all kinds of different events present in the sample space of a random device.

Figure 3 shows the random devices used in probability.

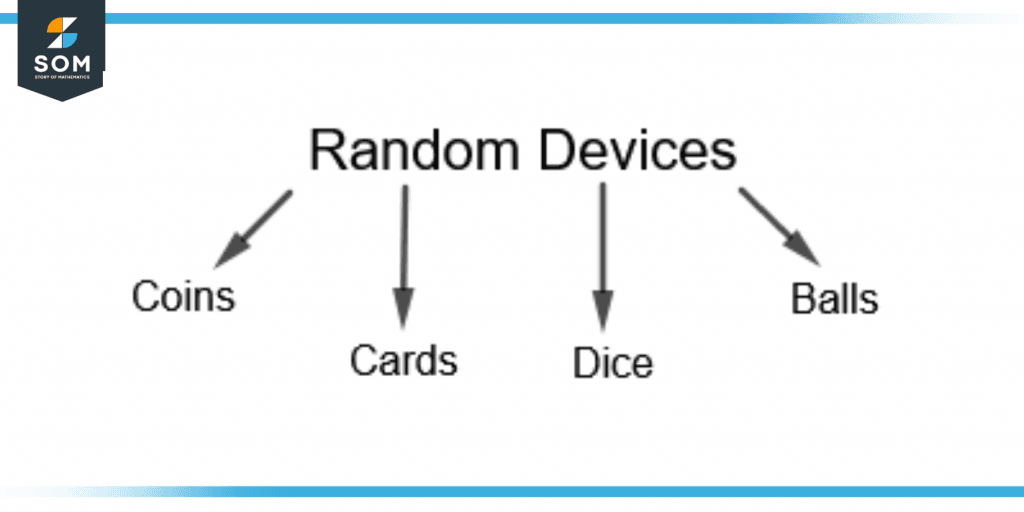
Figure 3 – Random Devices Used in Probability

Sample Space

Sample space is the set of all possibilities which can be obtained from a particular random device.  It is written in curly brackets and denoted by S.

For example, the sample space of a die are the six numbers which can be written as:

S = { 1, 2, 3, 4, 5, 6 }

Event

An event is a favorable outcome required from a random experiment. It is the subset of the sample space and is mostly denoted by E.

For example, the event for the numbers one and two turned up when a die is rolled can be written as:

E = { 1, 2 }

The probability for this event can be obtained by putting the values of n(S) and n(E).

Here,

n(S) = 6, n(E) = 2

Where n(S) is the number of outcomes in the sample space and n(E) is the number of desired outcomes for an event.

So, the probability of the particular event P(E) will be:

P(E) = n(E) / n(S) = 2 / 6 = 1 / 3 = 0.3

Types of Events

The value of probability explains what type the event will be. In mathematics, the probability is measured from 0 to 1 which shows the extent of the chance of an event occurring.

Following are the type of events classified by the measure of probability.

Impossible Event

An event is impossible to occur if its probability is zero. For example, the number seven occurring on a die has n(E) = 0 as the outcome is not included in the sample space.

The probability can be calculated as follows:

P(E) = n(E) / n(S) = 0 / 6 = 0

Unlikely Event

An event is unlikely to happen if its probability is between 0 and 0.5. The chance of an unlikely event occurring is small and increases from 0 to 0.5.

For example, a three occurring on a die has n(E) = 1 and n(S) = 6. The probability P(three) can be calculated as:

P(three) = n(E) / n(S) = 1 / 6 = 0.16

As the probability is less than 0.5 and more close to 0, the event is very unlikely to occur.

Evenly Chanced Events

Events are said to be evenly chanced when they have the same probability values. For example, all the numbers on a die have an equal chance of occurring i.e. 1 / 6 or 0.16.

A coin has the sample space:

S = { Head, Tail }

So,

n(S) = 2

For both, the head n(H)=1 and tail n(T)=1, the probabilities will be equal hence they are equally likely to occur.

P(H) = n(H) / n(S) = 1 / 2 or 0.5

P(T) = n(T) / n(S) = 1 / 2

As shown in figure 4, the evenly chanced events divide the probability scale into two equal parts.

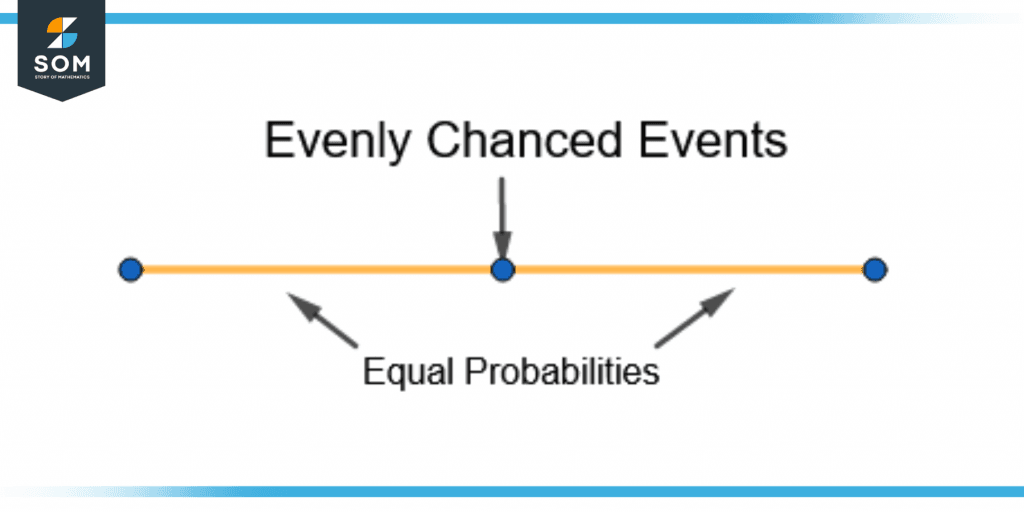
Figure 4 – Evenly Chanced Events on the Probability Scale

Likely Event

A likely event has a probability between 0.5 and 1. It is an event that has a greater chance of occurrence than an unlikely event.

For example, if the favorable outcome is E = { 1,2,3,4,5 } to occur on a die, the number of desired outcomes n(E) and the number of outcomes in the sample space n(S) are:

n(E) = 5

n(S) = 6

The probability for the event P(E) is given as:

P(E) = n(E) / n(S) = 5 / 6 = 0.83

Hence, the numbers 1, 2, 3, 4, and 5 are very likely to occur on the dice.

The likely and unlikely event range is shown on the probability scale in figure 5.

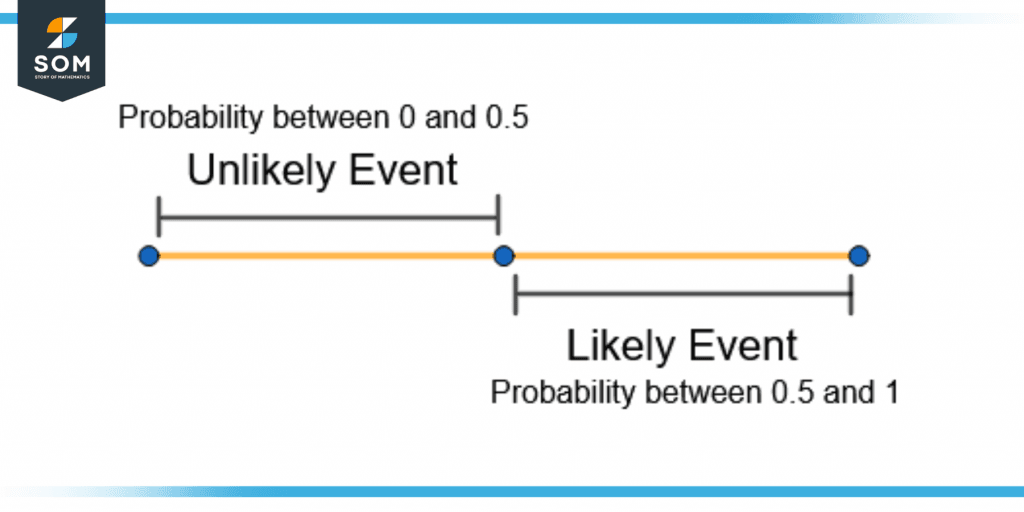
Figure 5 – Likely and Unlikely Events on the Probability Scale

Certain Event

An event is said to be certain if the value of probability is 1. This shows that the event is sure to happen.

An example of a certain event is obtaining a head or tail on a coin. Both n(E) and n(S) will be equal to 2, hence the probability P(E) will be:

P(E) = n(E) / n(S) = 2 / 2 = 1

Figure 6 shows the certain event and the impossible event as the boundaries on the probability scale.

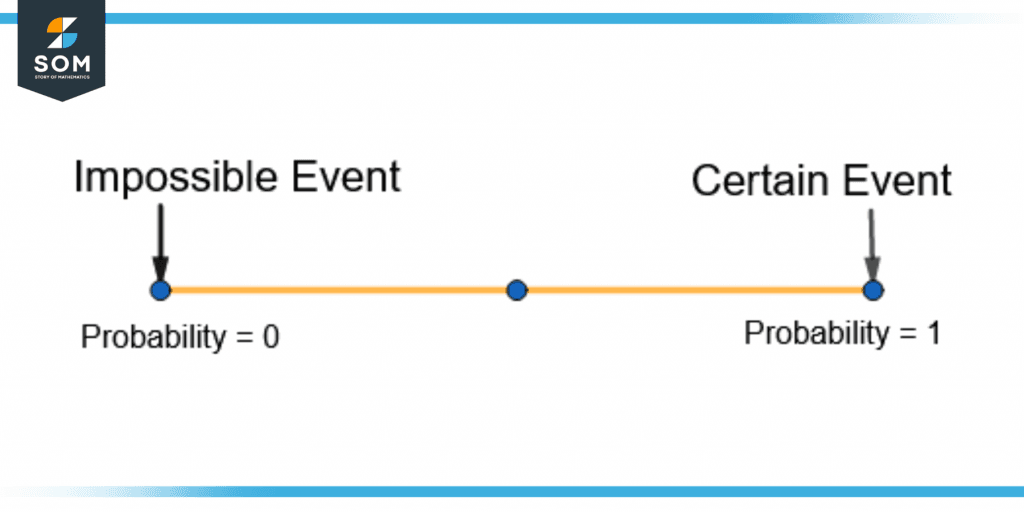
Figure 6 – Impossible and Certain Events on the Probability Scale

An Example of a Certain Event

Two dice are rolled. What is the probability of getting a product of 8 from the two numbers turned up on the two dice?

Solution

One die has 6 possible outcomes. As two dice are rolled, there are (6)(6) = 36 total possibilities that can occur. So,

n(S) = 36

Let E be the event for the two dice to turn up such numbers whose product is 8. These are (2,4) and (4,2) on the dice. So,

E = { (2,4), (4,2) }

Therefore,

n(E) = 2

So, the probability P(E) will be:

P ( E = product of 8 ) = n(E) / n(S) = 2 / 36 = 1 / 18 = 0.05

As it is close to zero and between 0 and 0.5, the event is very much unlikely to occur.

All the images are created using GeoGebra.

Center Centre Definition < Glossary Index > Chord Definition