Chord|Definition & Meaning

Chord of a Circle

Chord has been derived from the Latin word which is ‘Chorda’ meaning ‘Bowstring’. As the meaning of the word suggests that chord of a circle is a straight line that is drawn on the circumference of the circle containing its endpoints. A chord never passes through the center of the circle as both of its endpoints must remain on the outer boundary of the circle. Let us take this example of a circle: 

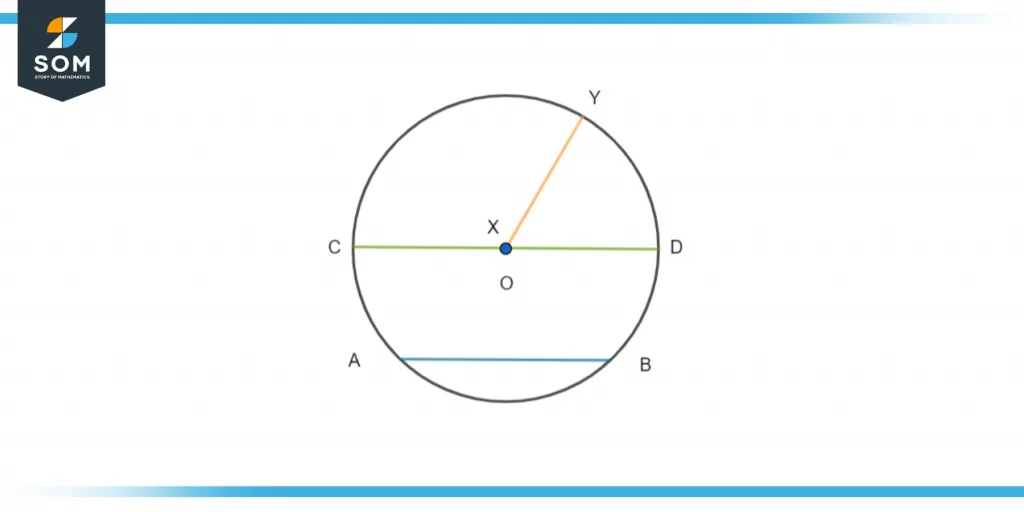
Figure 1 – The chord of a circle is shown along with the radius and diameter to help differentiate them

Here line AB represents the chord of the circle with center O. the line segment CD represents the diameter of the circle whereas line segment XY represents the radius of the circle.

Mathematical Representation

The line segment that links two points of a circle can be calculated to get the length. We are able to do this by using the radius of the circle and the length of the angle right bisector. For this, we will sketch a straight line perpendicular from the center of the circle to the line segment. This bisector will help us to find the length with the help of Pythagoras’s Theorem.

There are basic two ways to find the length of a chord. One method is by using the perpendicular which gives us this formula:

Chord Length = 2$\sqrt{r^2-d^2}$

And the other method is by using trigonometry:

Chord Length = 2 × r × sin(c/2)

Here, r is the radius of the circle, c is the angle of the chord, and d is the diameter of the circle.

Properties of Chord

Now let us take some notes on the properties of a chord and try to understand the relationship between different chords and the angles they subtend from the center of the circle:

1. Two equal chords will always subtend equal angles at the center of the circle.
2. Similarly, if the angles subtended by two chords are equal then the corresponding chords will also be of equal length.
3. All chords of a circle that is equal in length will be equidistant from the center of that circle.
4. The radius of any circle always bisects the chord at 90°.
5. When two radii link the two endpoints of the chord then we get an isosceles triangle.
6. In any circle, the diameter is considered the longest chord and it passes through the center of the circle.
7. The extension of any chord is called a secant. If any 2 secants intersect at some point then the chords are considered equal.

Relationship Between Chord and Radius

The chord and Radius of a circle are related in such a way that if in a circle we have to calculate the radius circle all we will need is the height and length of the circle. This shows how related these two are. To get the radius we will multiply the height of the chord 4 times and will square its length.

Similarly to get the values of the chord we can use the value of the radius along with the value of the diameter to get our desired answer.

Theorems of Chord of a Circle

Following are theorems related to the chord of the circle which will help you with the concepts.

Theorem 1

Any perpendicular that extends from the center of the circle bisects the chord

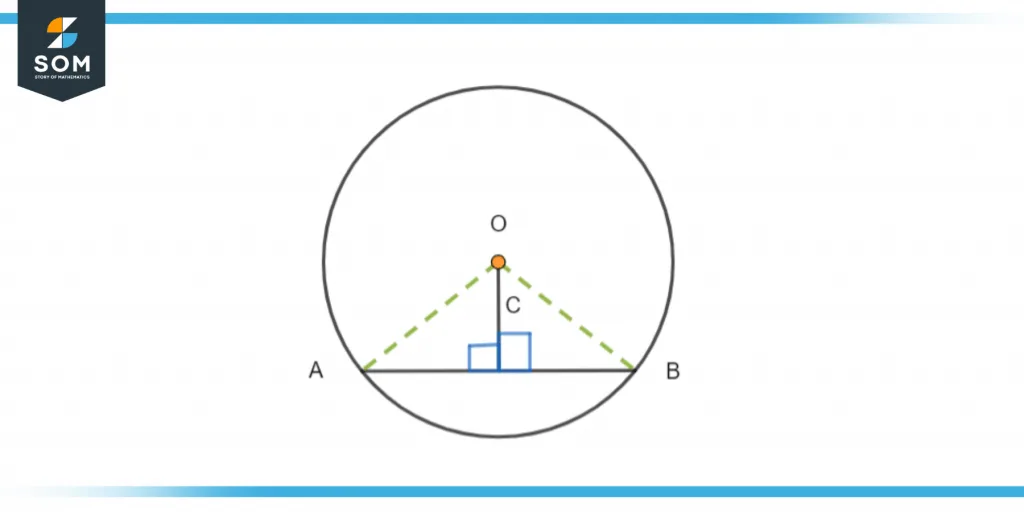
Figure 2 – A chord AB in a circle with center O

In this theorem, we will prove whether both the angles subtended by the perpendicular OC from the center of the circle are equal. 

For this purpose, we have joined O to A and O to B. now we can solve it.

In ∆OAC and ∆OBC

AC = BC 

As the perpendicular intersects in the middle. Then we can also say that:

OA = OB 

This is because they both are the radii of the circle.

OC = OC 

This is because they are common in both triangles. Hence by SSS postulates, we can call both ∆OAC and ∆OBC congruent. Now:

 ∠ OCA = ∠ OCB

So,

∠ OCA + ∠ OCB = 180°

As they are a linear pair. Then we can say that:

∠ OCA = ∠ OCB = 90°

Hence we have proved that: 

OC ⊥ AB

Theorem 2

Equal Chords in length subtend equal angles at the center of the circle.

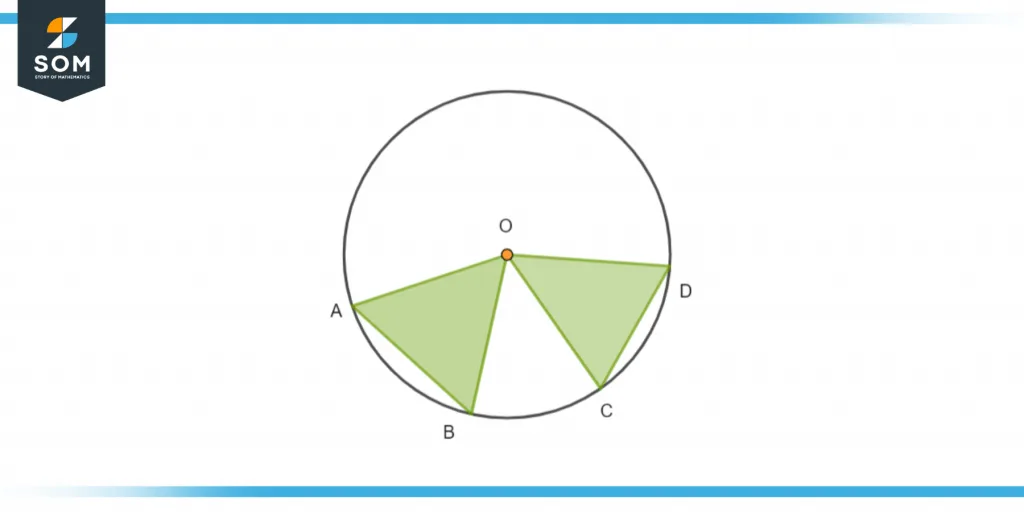
Figure 3 – Two chords that subtend equal angles in a circle with center O

In this theorem, we have to prove that chords that are equal in length always subtend equal angles.

In ∆AOB and ∆COD

AB=CD

This is because these are the chords of the circle which is of equal length.

OA = OB = OC = OD

These all represent the radius of the circle as each has an endpoint on the circumference of the circle and the other endpoint is at the center of the circle.

△AOB ≅ △COD

By using the SSS axiom of congruence we have proved these two triangles to be congruent to each other.

∠AOB = ∠COD

Hence, we have proved this theorem by congruent parts of the congruent triangles statement.

Theorem 3

Equal chords of a circle are equidistant from the center of the circle.

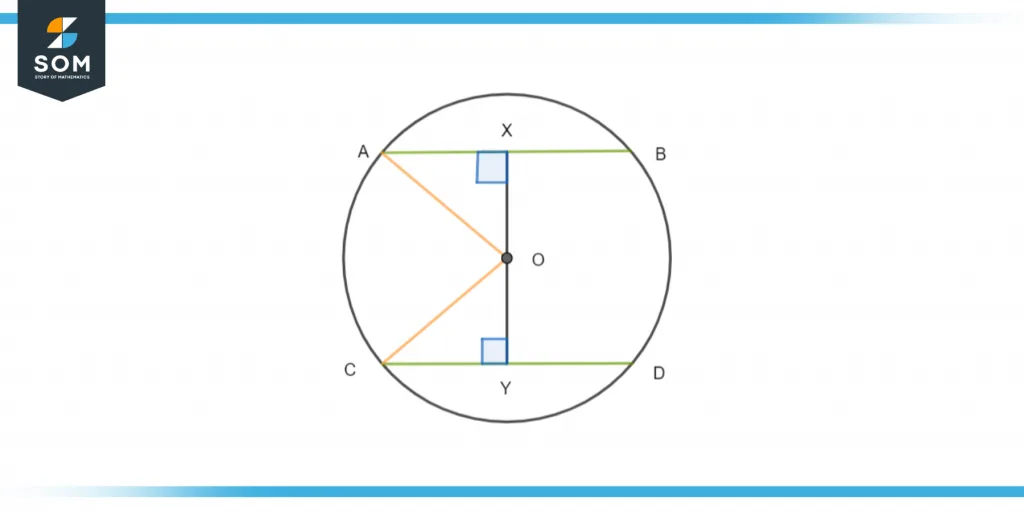
Figure 4 – A circle with two chords AB and CD

We will join O to A and O to C and from the center of the circle, we will extend perpendiculars towards both chords such that one will intersect CD at point Y and the other will intersect AB at point X. 

AX = AB/2 and CY = CD/2

As we know that the perpendicular bisects the chord.

In △OAX and △OCY:

∠1 = ∠2 = 90°

We have constructed that OX⊥AB and OY⊥CD:

OA = OC

They are the radii of the same circle:

OX = OY

It was given in the statement of the theorem:

△OXB ≅ △OYD

These two triangles are congruent under the R.H.S congruence axiom:

AX = CY

As they are corresponding parts of a congruent triangle hence:

AB = CD

Solved Examples of Chord

Example 1

From the given figure calculate ∠AOC when the value of ∠ABC is 42°.

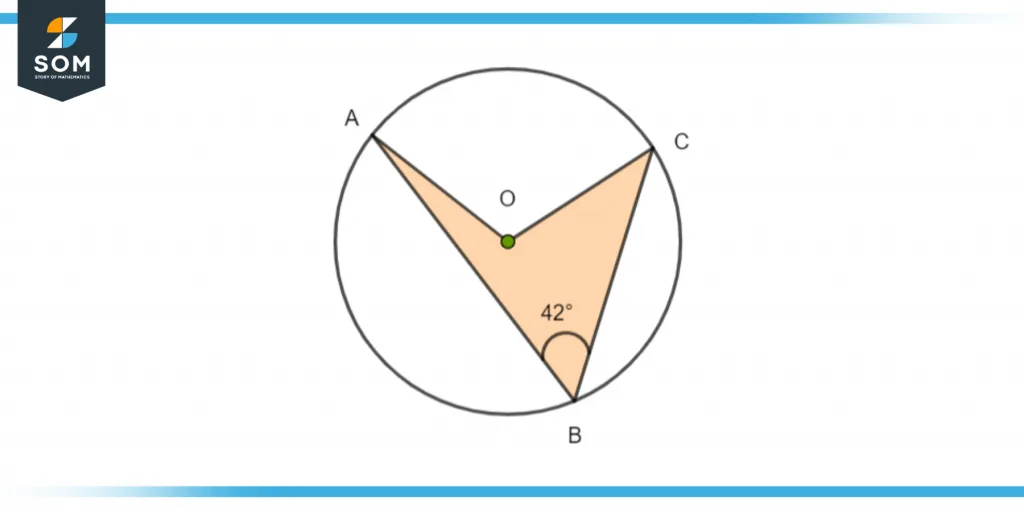
Figure 5 – A circle that forms an angle by the intersection of 2 chords at a point

Solution

As we know from the theorem, the angle given at the center of the circle by an arc will be considered twice the size of the angle subtended by it at any point on the circumference of a circle.

Hence, ∠AOC is equal to two times ∠ABC.

 Therefore:

∠AOC = 2 x ∠ABC

∠AOC = 2 x 42° = 84°

Images/mathematical drawings are created with GeoGebra.

Certain Definition < Glossary Index > Circle Definition