Circumcenter|Definition & Meaning

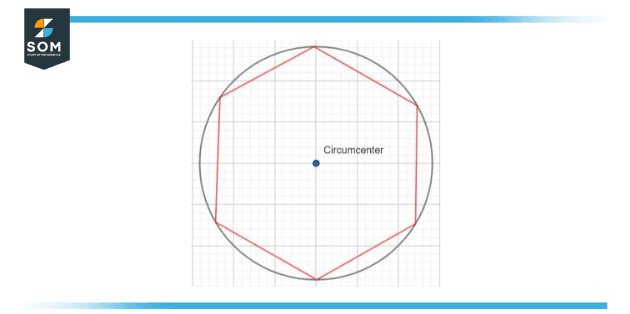
Figure 1 – The circumcenter of a 6-sided polygon 

The circumcircle of a polygon in geometry is a circle that passes through all the polygon’s vertices. The center of this circle is known as the circumcenter and its radius is named as the circumradius.

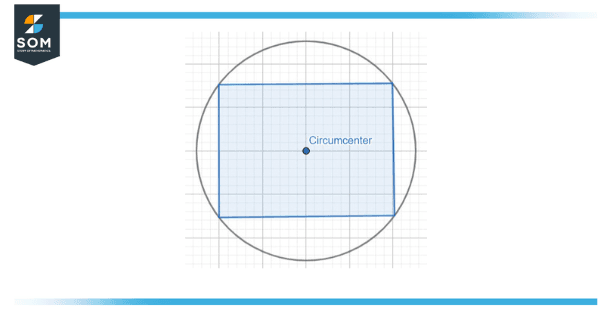
Figure 2 – The circumcenter of a 4-sided polygon

The circumcenter of a triangle is described as the juncture where the perpendicular bisectors of the sides of the triangle cross. The circumcenter is the point of concurrence of the bisector of the triangle’s sides. It is characterized by P(X, Y). The circumcenter is likewise the middle of the circumcircle of that triangle. The circumcenter of the triangle can either be inside or outside the triangle.

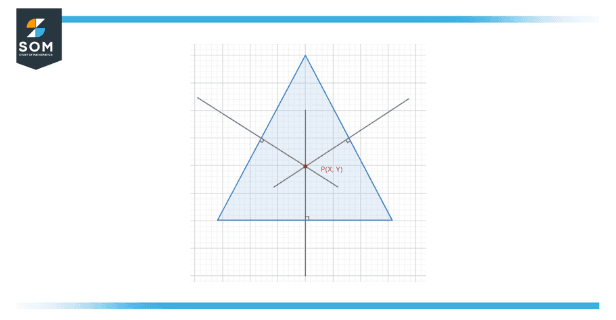
Figure 3 – The circumcenter of a Triangle

What is the Circumcenter of Triangle

The circumcenter in geometry is the juncture at which the three perpendicular bisectors of the triangle’s side meet, and the length from each of the three triangle vertices is exactly the same.

The circumcenter of a  triangle is the point where three perpendicular bisectors from the triangle’s sides bisect or meet. The circumcenter of a triangle is also called the point of concurrence of a triangle. The juncture of origin of a circumcircle is a circle etched inside a triangle also named as the circumcenter.

The circumcenter of the triangle can be figured out as the conjunction of the perpendicular bisectors that is the lines that are at right angles to the middle of each side of all flanks of the triangle. This indicates that the perpendicular bisectors of the triangle are concurrent which means that they meet at one point. All triangles are cyclic and thus, can circumscribe a circle, consequently, a circumcenter is found in every triangle. To produce the circumcenter of a triangle, perpendicular bisectors of any two flanks of a triangle are marked.

Circumcenter and Circumcircle

The circle cannot be circumscribed in every polygon. A cyclic polygon is a polygon that does have one. cyclic polygon is sometimes called as a concyclic polygon because of its concyclic vertices. All triangles, all rectangles, all regular simple polygons, all right kites, and all isosceles trapezoids are cyclic.

An associated idea is the one of a lowest bounding circle, which is the most undersized circle that fully contains the polygon inside of it if the center of the circle is within the polygon. Every polygon has a distinctive lowest bounding circle, which may be formed by a linear time algorithm. Actually, if a circle is circumscribed within the polygon then it might be distinct from
its minimum bounding circle. For instance, for an obtuse triangle, the lowest bounding circle has the most extended side as a diameter and does not cross through the opposing vertex.

Properties of Circumcenter

Following are some of the properties of the circumcenter of the triangle:

• The circumcenter lies in the center of the circumcircle.
• All the triangle’s vertices are equidistant from the circumcenter.
• The circumcenter lies inside the triangle in an acute triangle.
• The circumcenter lies outside of the triangle in an obtuse triangle.

Method to Calculate the Circumcenter of a Triangle

Following are steps to find the circumcenter of a triangle:

1. Compute the midpoint of given coordinates, for example, midpoints of AB, BC, and AC.
2. Compute the slope of the respective line.
3. By utilizing the midpoint and the slope, figure out the equation of the line which is y – y₁ =m(x – x₁)
4. figure out the equation of the other line in the same way.
5. Compute two bisector equations by estimating t the intersection point
6. The calculated meeting point will be the circumcenter of the provided triangle.

Finding Circumcenter Using Linear Equations

The circumcenter can be estimated by constructing linear equations utilizing the distance formula. Let us consider circumcenter has the coordinates of (X, Y). According to the properties of the circumcenter , the length of (X, Y) from each vertex of a triangle will be the exact same.

Assume that D₁ is the length between circumcenter (X, Y) and the vertex is (x₁, y₁), then the formula is presented by,

D₁ = $\sqrt{(X-x_1)^2 + (Y-y_1)^2}$

D₂ = $\sqrt{(X-x_2)^2 + (Y-y_2)^2}$

D₃ = $\sqrt{(X-x_3)^2 + (Y-y_3)^2}$

Now, since D₁=D₂ and D₂=D₃, we get

\[ \sqrt{ (X-x_1)^2 + (Y-y_1)^2} = \sqrt{ (X-x_2)^2 + (Y-y_2)^2} \]

Two linear equations are acquired from this and by simplifying the linear equations by utilizing the elimination or substitution method, the coordinates of the circumcenter can be acquired.

An Example of Finding the Circumcenter

The vertices of a triangle ABC are given as A = (2, 2), B = (0, 4), and C = (4, 4), find the coordinates of its circumcenter ?

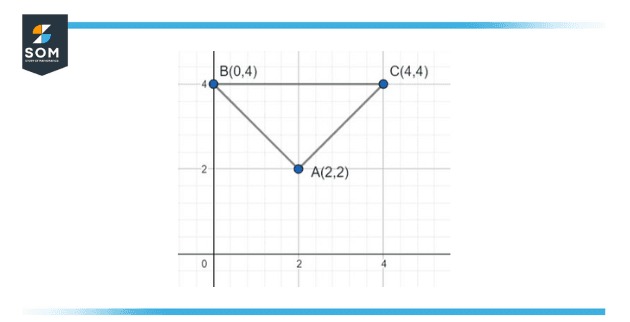
Figure 4 – Finding the circumcenter of a triangle.

Solution

Suppose P(x, y) to be the coordinates of the circumcenter,

D₁ be the length from the vertex A to the circumcenter,

D₂ be the length from the vertex B to the circumcenter,

and D₃ be the length from the vertex C to the circumcenter.

Given the vertexes are: A(x₁, x₁) = A(2, 2), B(x₂, x₂) = B(0, 4), and C(x₃, x₃) = C(4, 4).

Using the euclidean distance formula:

D₁ = $\sqrt{(X-x_1)^2 + (Y-y_1)^2}$

D₂ = $\sqrt{(X-x_2)^2 + (Y-y_2)^2}$

D₃ = $\sqrt{(X-x_3)^2 + (Y-y_3)^2}$

Since D₁= D₂ = D₃.

D₁ = D₂ gives:

\[ \sqrt{(X-2)^2 + (Y-2)^2} = \sqrt{(X-0)^2 + (Y-4)^2} \]

Squaring the above gives the following:

x² + 4 – 4x  + y² + 4 – 4y  = x² + y² + 16 – 8y

-4x – 4y + 8 = 16 – 8y

-4x – 8 + 4y = 0

4y – 4x = 8

-x + y = 2

D₁ = D₃ gives:

\[ \sqrt{(X-2)^2 + (Y-2)^2} = \sqrt{(X-4)^2 + (Y-4)^2} \]

Squaring both sides, we get:

x² + 4 – 4x + y² + 4 – 4y = x² + 16 – 8x + y² + 16 – 8y

8 – 4x – 4y = 32 – 8x – 8y

4x + 4y = 24

x + y = 6

By solving both equations, we get:

2y = 8

y = 4

Now, plugging y = 4 in other equation,

x + 4 = 6

x = 2

Hence, the circumcenter of a triangle is (x, y) = (2, 4).

All images/mathematical drawings were created with GeoGebra.

Circle Definition < Glossary Index > Circumference Definition