JUMP TO TOPIC
Circumference|Definition & Meaning
Definition
A circle’s circumference is the length of its perimeter. The circle circumference can be determined by using length units such as centimeters, meters, or kilometers by opening a circle and measuring the boundary in the same way that we would measure a straight line.
A circle’s perimeter is known as its circumference. It is the circumference of the circle as a whole. A circle’s circumference is calculated by multiplying its diameter by the constant. This measurement of a circle’s diameter is necessary for someone crossing a circular park or for enclosing a circle. The units for the circumference, which is a linear variable, are the same as those for length.

Figure 1 – Circumference of a circle
A circle is a closed, rounded shape whose border points are all equally spaced apart from the center. The diameter and area of a circle are two crucial measurements of a circle. Here, our goal is to comprehend the formula and computation used to determine a circle’s circumference.
The Formula of a Circumference of a Circle
Using the circle’s radius (r) and the number “pi” one may calculate the circumference of a circle. The circumference of a circle formula = 2$\pi$r is how it is stated. If we do not know the radius’s value while utilizing this circumference formula, we can calculate it using the diameter.
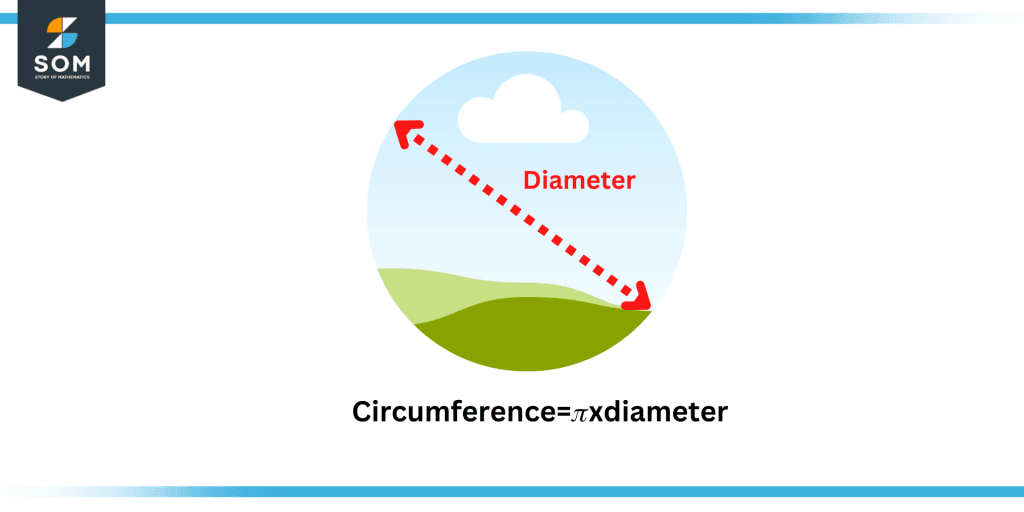
Figure 2 – Circumference diameter relation
Since the diameter of a circle equals twice the radius, we can divide the former by 2 to determine the value of the radius. The equation Circumference = Diameter x $\pi$ $\pi$ can also be used to determine a circle’s circumference. When the circumference of a circle is known but we need to determine the radius or diameter, we apply the following formula:
radius = circumference / (2$\pi$)
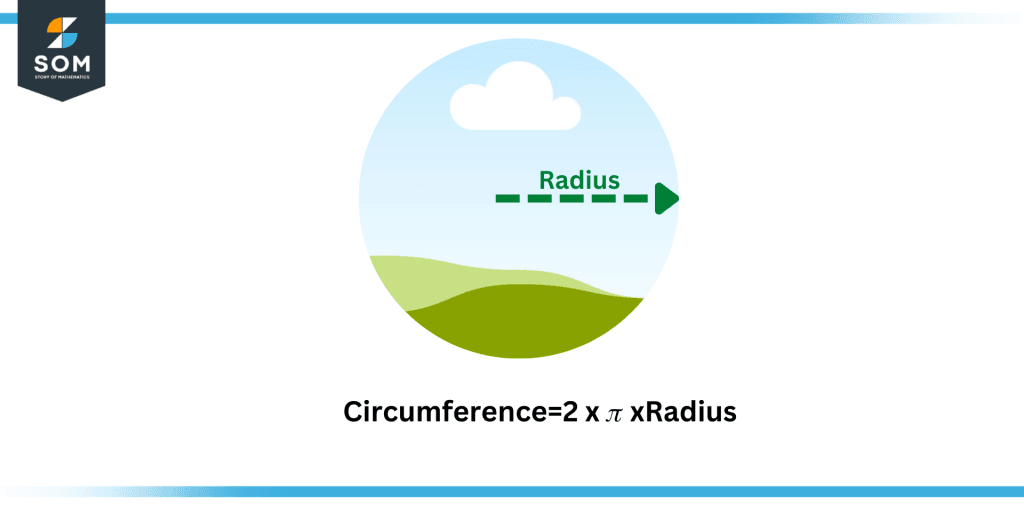
Figure 3 – Circumference radius relation
How To Calculate the Circumference?
Method 1: Since a circle is a curved surface, it is impossible to physically measure its length with a scale or ruler. However, polygons like squares, triangles, and rectangles can be made in this way. Instead, we can use a thread to calculate the circumference of a circle. Use the thread to trace the circle’s route, marking the points as you go. A typical ruler can be used to measure this length.
Method 2: Calculating a circle’s circumference is an accurate approach to determining its size. The circle’s radius must be specified for this. The radius is the distance from any point on the circle’s circumference to its centre. The circle with radius R and center O is depicted in the figure below. The circle’s radius is equal to twice its diameter.
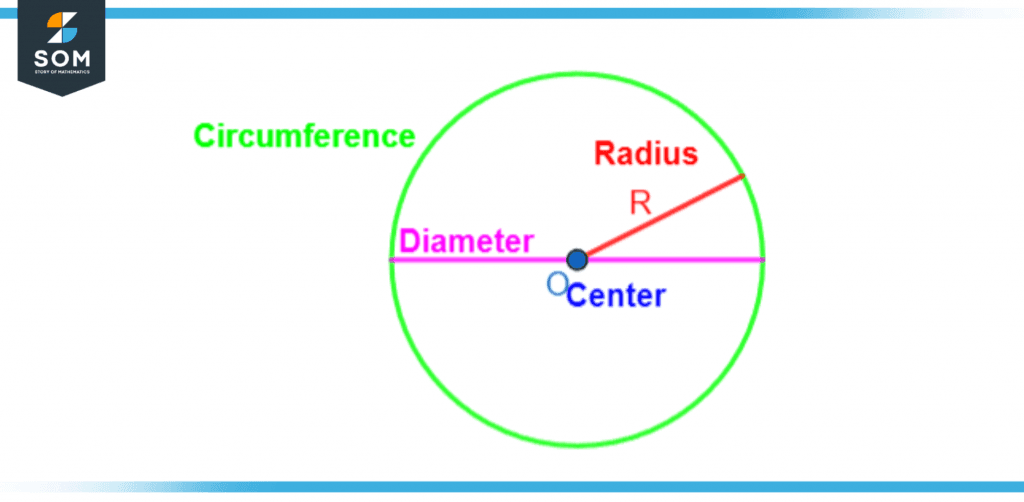
Figure 4 – Major parameters of a circle
Let’s now discover the components of circumference. The three most crucial components of a circle are these three.
Circle: A circle’s center and radius make up its 2D shape. If we are aware of the circle’s center and radius, we can draw any circle. The radii of a circle are infinitely variable. The midpoint where all of the radii meet is the center of a circle. The center of the circle’s diameter is another way to describe it.
Radius: Any circular object’s radius is the measurement from the center to its outermost border or boundary. A radius is a dimension that applies to spheres, semi-spheres, cones with circular bases, and cylinders with circular bases in addition to circles.
It is possible to define a circle as the locus of a point traveling on a plane while maintaining a constant distance from a fixed point. The radius, as mentioned earlier, is the distance from any point on the circumference to the center. The fixed point is referred to as the center of the circle.
Diameter: The radius of a circle is multiplied by two to get its diameter. While the radius is measured from a circle’s center to one endpoint on its perimeter, the diameter is measured from one end of a circle to any other point on the circle as long as it passes through the center. The letter D is used to identify it.
There are endless points on the circumference of a circle, which translates to an endless number of diameters with equal lengths for each diameter.
Important Notes About a Circle’s Circumference
- The ratio of a circle’s diameter to circumference is known as (Pi) in mathematics. It is about equal to = 22/7 or 3.14
- A circle’s diameter is created when a circle’s radius is expanded until it meets the circle’s edge. Therefore, Diameter = 2 x Radius
- The circumference is often known as the length of a circle.
- By using the radius or diameter, we may calculate the circumference of a circle.
- Circumference formula = Diameter x $\boldsymbol\pi$
Some Examples of Finding the Circumference
Example 1
A rectangular wire has a 540 m perimeter. The same wire is bent into a circle. Using the circumference formula, determine the radius of the produced circle.
Solution
Since the circumference of the circle formed equals the total length of the wire utilized equals the perimeter of the rectangle.
Consequently, the circle’s circumference is 540meters.
The formula for the circumference of a circle is 2$\pi$r.
The circle’s circumference is 540.
To determine the radius, let’s substitute the known numbers.
Circumference = 540
= 2$\pi$r
r=540/2$\pi$
Consequently, the circle’s radius is 85.9 meters.
Example 2
Find the 10 cm radius circle’s area and perimeter. [Note: $\pi$ = 3.14]
Solution
The circle’s perimeter and area have to be determined.
Consequently, Radius, r = 10 cm, and $\pi$= 3.14
A circle’s perimeter (or circumference) equals 2$\pi$r units
A circle has an area of $\pi$r $^{2}$ square units.
When we change the values in the formula for the perimeter and area of a circle, we obtain
The circle area is equal to $\pi$r$^2$= 3.14x10x10.
A = 3.14 x 5 x 5
A = 78.5 cm$^2$
The circle’s circumference equals 2 x 3.14 x 10 = 62.8 cm.
Thus, the circle’s circumference and area are 62.8 cm and 314 cm$^2$, respectively.
Example 3
Find the circumference of a circle with a radius of 45 cm.
Solution
Given that, the circle’s radius is 45 cm. We shall use the following formula to determine the circle’s circumference: 2$\boldsymbol\pi$r = 2 x 3.14 x 45 = 282.6 cm.
The circle’s circumference is 282.6 cm as a result.
All images/mathematical drawings were created with GeoGebra.
