Circumradius|Definition & Meaning

Building Concept for Circumradius

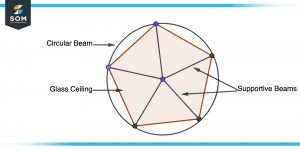
Figure 1 – Illustration of Concepts for Understanding Circumradius

A glass ceiling is shaped like a pentagon with equal sides, and an architect designs it so that it is dome-shaped and has a beam of a circle around it. As depicted in the figure, the designer realizes that each of the pentagonal windows will need to have supportive beams going from its vertex to the mid(center) of the beam of the circle when designing the glass ceiling.  

Circumcircle

Mathematics is actually a fascinating subject when we talk about this pentagonal glass ceiling and its circular beam. As a result of passing through each vertice of a polygon, a circumcircle is a circle drawn around it. The circular beam constitutes the circumcircle in this example, while the Polygon is represented by a pentagonal ceiling.

Circumradius

Polygons with circumcircles also possess a circumradius, which is another important characteristic. An arbitrary polygon’s circumradius is the radius of the circle inside which the polygon is inscribed. In other words, it is a line segment that connects any vertex of the polygon to the circumcircle’s center.

There is a circumradius on each triangle and tetrahedron, but not for all polygons or polyhedra. The few polygons that have a circumradius are regular polygons. 

Circumradius vs Inradius

The circumradius and inradius of a triangle are different types of radii. When a triangle is circumscribed by a circle, then the circumradius is the radius of that circle. In a triangle, the circumcenter is where all three vertices of the triangle touch, and these points are called the triangle’s vertices. Alternatively, an inradius indicates the distance between the triangle-enclosed circle’s center and the tangent point of that triangle.

Circumradius of Triangle

From the vertices of the triangles, we calculate the circumradius, which is equal to the distance between them and the circle’s center. Circumcircle is another name for this circle. This is shown in the figure below.

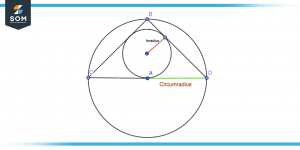
Figure 2 – Triangle Circumradius

Euler Theorem

According to Euler’s triangle theorem, the circumradius and inradius of a triangle are related to the distance between their centers.

Let r be the inradius (intersection point of all three vertices of the triangle).

Let R be the circumradius (When a triangle is circumscribed by a circle, then the circumradius is the radius of that circle).

Let the distance between the circumcenter(R) and incenter(r) be d. We can write

$d^{2}=R(R-2r)$

The Formula of the Circumradius of the Triangle

Suppose the sides of the triangle as a, b, and c and we want to find the circumradius so we can write it as:

Circumradius of Triangle =$\dfrac{abc}{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} $

Finding Circumradius of Triangle Practically

There are relatively few steps involved in the construction of a circumradius. Compass and straight edge are the only materials you’ll need.

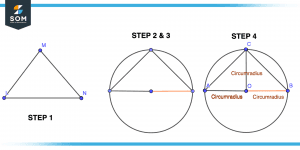
Figure 3 – Constructing Circumradius of Triangle Practically

Step 1

Draw a triangle with three vertices L, M, and N.

Step 2

The next step is to draw a circle that touches every vertex or side of the triangle. The circumcircle can be seen here. This circle has a circumcenter in its center.

Step 3

From one of the three vertices, draw a segment around the circumcenter. Measurement of the circumradius is based on the length of this line segment.

Step 4

Join every vertex of the triangle with point O so that we get OA, OB, and OC. OA, OB, and OC are known as circumradii of the triangle shown in the figure.

Circumradius of Regular Polygon

In euclidean geometry, a regular polygon is one that is direct equiangular. This means that all angles are equal in measure, and equilateral means all sides have the same length.

Consider the following polygon having each vertex of the same length and a circle is present inside which the polygon is inscribed. The line segment from the center of that circle meeting on any end of the polygon vertex is known as a circumradius as shown in the figure.

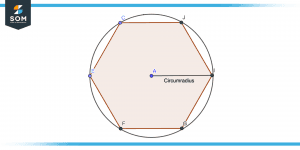
Figure 4 – Regular Polygon Circumradius

The Formula of Circumradius of a Regular Polygon

Let a be each vertex of the polygon being equal in length and n is the number of the vertex in the polygon then the circumradius of a polygon can be written as:

Circumradius of Regular Polygon =$\dfrac{a}{2\sin\frac{\pi}{n}}$

Circumradius of Cyclic Quadrilateral

Cyclic quadrilaterals can be scribed into circles by inlaying four sides. Quadrilaterals have four chords connecting their vertex to the circle circumference. The radius of that circle is known as the circumradius of that cyclic quadrilateral. Below is an illustration of the concept.

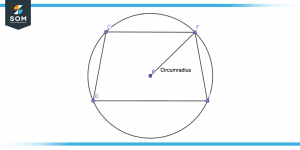
Figure 5 – Cyclic Quadrilateral Circumradius

The Formula of Circumradius of Cyclic Quadrilateral

Consider a cyclic quadrilateral having four vertex AB, BC, CD, and DA, and suppose that

a = AB, b = BC , c = CD and d = DA

We can write the formula for the semi-perimeter (which will later be used in circumradius)

Semiperimeter of cyclic quadrilateral = $\displaystyle\frac{a+b+c+d}{2} $

From this, we can write the formula for cyclic quadrilateral as 

Circumradius of cyclic quadrilateral = $\displaystyle\frac{1}{4} \times \sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}$

Some Examples of Finding the Circumradius

Example 1

Consider a Triangle with sides a=5cm, b=6cm, c=7cm, and a circle is circumscribed. Find the circumradius.

Solution

Circumradius R = $\dfrac{abc}{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} $

Circumradius R = $\dfrac{5 \cdot 6 \cdot 7}{\sqrt{(5+6+7)(6+7-5)(7+6-5)(5+6-7)}}$

Circumradius R = $\dfrac{210}{\sqrt{(18)(6+7-5)(7+6-5)(5+6-7)}} $

Circumradius R = $\dfrac{210}{\sqrt{(18)(8)(8)(4)}}$

Circumradius R = $\dfrac{210}{\sqrt{(4608)}} $

Example 2

Consider six sides of regular polygon AB, BC, CD, DE, EF, and FG, which are equal in length. Find the circumradius.

Solution

We are given the data:

a = 5 cm

n = 6

Circumradius R = $\dfrac{a}{2\sin\frac{\pi}{n}} $

Circumradius R = $\dfrac{5}{2\sin\frac{\pi}{6}} $

Circumradius R = $\dfrac{5}{2 \times 0.00913} $

Circumradius R = $\dfrac{5}{0.0182} $

Example 3

Consider a cyclic quadrilateral with a=3, b=4, c=5, and d=6 find the circumradius.

Solution

First we will find semiperimeter:

Semiperimeter = $\dfrac{3+4+5+6}{2} $

Semiperimeter = $\dfrac{18}{2} $

Semiperimeter = $9$

Circumradius R = $\displaystyle\frac{1}{4} \times \sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}} $

Circumradius R = $\displaystyle\frac{1}{4} \times \sqrt{\frac{(3 \times 4+5 \times 6)(3\times 5+4\times 6)(3\times 6+4\times 5)}{(9-3)(9-4)(9-5)(9-6)}} $

Circumradius R = $\displaystyle\frac{1}{4} \times \sqrt{\frac{(12+30)(15+24)(18+20)}{(6)(5)(4)(3)}} $

Circumradius R = $\displaystyle\frac{1}{4} \times \sqrt{\frac{(42)(39)(38)}{360}} $

Circumradius R = $\displaystyle\frac{1}{4} \times \sqrt{\frac{62244}{360}} $

Circumradius R = $\displaystyle\frac{1}{4} \times 13.149 $

Circumradius R = $3.28$

All mathematical drawings and images were created with GeoGebra.

Circumference Definition < Glossary Index > Class Interval Definition