Closed Intervals|Definition & Meaning

Other intervals are any singleton, the set of all real numbers $\mathbb{R}$, the set of nonnegative real numbers, real numbers of a positive set, the empty set, and the set of values such as 0 $\leqslant$ x $\leqslant$ 1 (set of one element).  

What Is Meant by Interval Notation?

Interval Notation is a technique of representing a subset containing real numbers by the numbers that connect them. Inequalities can be represented using this notation. We know that an interval expressed as 1 $\leqslant$ x $\leqslant$ 6 denotes a set of numbers ranging from 1 to 6. Figure 1 shows us closed intervals can be represented:

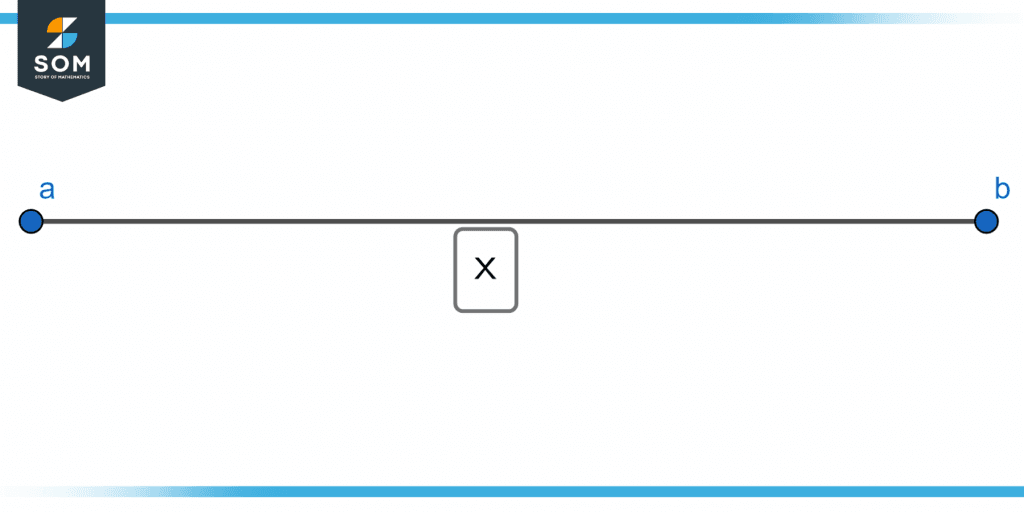
Figure 1 – Representation of a closed interval on a number line.

Based on the numbers in the set, intervals can be categorized. Some sets have the endpoints indicated in the notation, but others may only contain them partially or not. There are generally three different sorts of intervals:

• Closed Intervals
• Open Intervals
• Half-Open Intervals

Explaining Open and Closed Intervals

A range of numerical values is represented by an open interval and a closed interval. Only the values between the endpoints are included in the open interval, shown as ( ). The closed interval is denoted by [ ] and contains even the range’s extreme values. The following figure 2 shows both open and closed intervals:

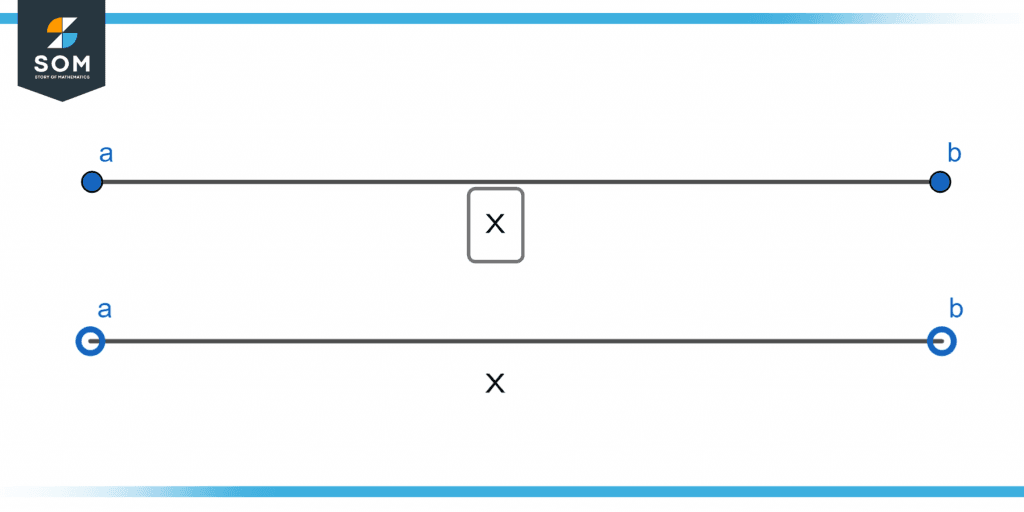
Figure 2 – Representation of open and closed intervals on a number line.

For example, if we look at the range of numbers between 5 and 15, the open interval will contain all the values between the numbers 5 and 15, excluding 5 and 15. This can be written as (5, 15) or 5 $<$ x $<$ 15. However, if we take the same range for a closed interval, the values would be all the numbers between 5 and 15, including 5 and 15. It can be represented as [5, 15] or 5 $\leqslant$ x $\leqslant$ 15.

Differences Between Closed and Open Intervals

Based on the interval’s endpoints, it is possible to comprehend the distinction between an open and closed interval. The following list highlights some key differences between the open and closed intervals:

• The endpoints are included in the closed interval but not in the open interval.
• (a, b) is used to represent the open interval, and [a, b] is used to describe the closed interval.
• A closed interval is represented by the expression a $<$ x $<$ b and an open interval by a $\leqslant$ x $\leqslant$ b.
• The closed interval has a darkened dot at the end, while the open interval on the number line has two circles at its ends.

Half-open Intervals

Half-Open intervals only occur at one point of the number line, either the starting number or the ending number. The half-open interval explains that one of the interval points is to be added to the range.

We represent a Half-open interval as [a, b) or (a, b], which means that the range of the number line can be written as a $\leq$ x $<$ b, or a $<$ x $\leq$ b. The following figure shows how the open-half intervals are operated:

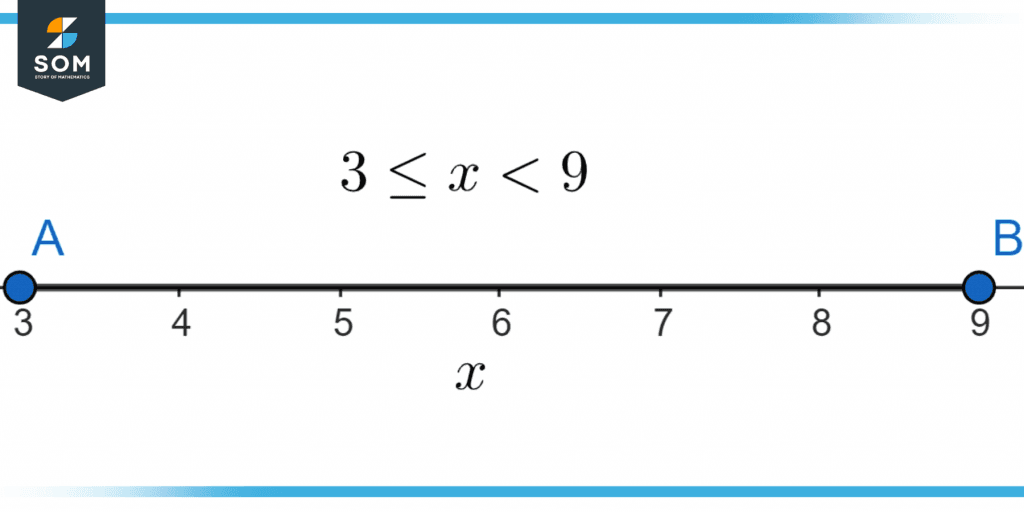
Figure 3 – Half-open intervals on a number line.

Real-Life Applications of Closed Intervals

We use closed intervals daily in our life. Here are some real-life examples and applications of closed intervals:

• A pencil can cost anything from \$3 to \$5. As the cost values are \$3 to \$5, the price of a pencil set can be priced anywhere from \$3 and \$5. This is an example of closed intervals.
• Students between the ages of 4 and 7 are eligible for entrance, and this includes children between the ages of 4 and 7. This is an illustration of a closed interval since it covers pupils between the ages of 4 and 7.

A Few Examples of Closed Intervals

Below are some solved examples that would help you further understand the concept of closed intervals.

Example 1

For a country’s Prime Minister, a person must be at least 35 years old. The maximum age for being elected prime minister is 60. Using the concept of closed intervals, find a range of ages for the candidates.

Solution

We can consider the age of the person applying for the position as X. Looking at the information provided in the question, we know that the minimum age for being eligible to be the Prime Minister is 35, and the maximum age is 60.

Hence, we can write the eligibility criteria as [35, 60]. This interval notation is known as closed intervals, clearly showing the minimum and maximum age for applying for Prime Minister.

This closed interval is represented by the following range:

35 $\leqslant$ X $\leqslant$ 60

Example 2

A footballer needs a minimum of 1500 and a maximum of 2500 calories per day to maintain his desired fitness level. Show the number of calories the football player cannot exceed using interval notation.

Solution

We can consider the number of calories the football player intakes as C. Using the information given in the question, and we know that the minimum number of calories the player needs per day is 1500. We also know that the player cannot exceed 2500 calories per day. 

Hence, we can use this information to write an interval notation which is [1500, 2500]. The interval notation used is closed intervals. And it represents that the player can have a minimum of 1500 calories and a maximum of 2500 calories per day. We can also write this information in the following format:

1500 $\leqslant$ C $\leqslant$ 2500

Example 3

For a school to participate in a science olympiad, they must have a team of a minimum of three students. The members of a team cannot exceed five students. What will be the interval notation of the members of the team representing the school?

Solution

We first consider the number of students as S. By analyzing the information in the question, we know that the minimum number of students in a team must be three, and the number of students in a team cannot exceed five.

Therefore, we use this data to write the interval notation [3, 5]. The type of interval notation is closed intervals, representing the minimum and the maximum number of students in a team. We can also represent this information in the following manner:

3 $\leqslant$ S $\leqslant$ 5

All images/tables are made using GeoGebra.

Clockwise Definition < Glossary Index > Cluster Definition