Coincident|Definition & Meaning

By coinciding, we mean that it occurs simultaneously. The mathematical definition of coincidence is two lines lying adjacent to each other. We see them as a single line rather than multiple lines when they are arranged in this way. 

Representation of Coincident Line

Consider A1, B1, and C1, D1 to be the two lines when we place the two lines exactly on one another so that it looks like an overlap of two lines then the line is said to be coincident as shown in the figure below.

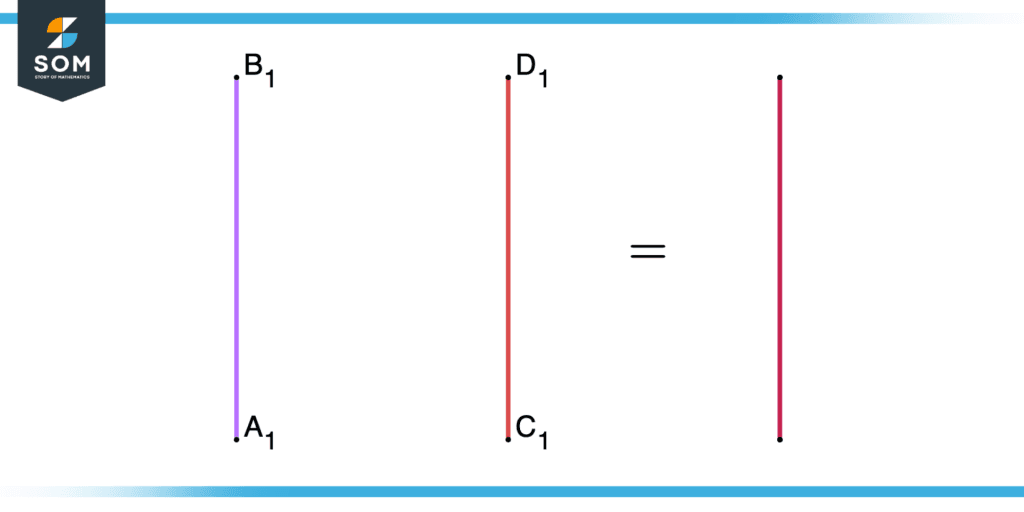
Figure 1 – An illustration of coincident lines. The color of line $\overleftrightarrow{A_{1}B_{1}}$ mixed with the color of $\overleftrightarrow{C_{1}D_{1}}$ produces the rightmost line.

As you can see from the above diagram, there have been two parallel lines drawn together, but they seem to be a single line when viewed from the top, but they are two distinct lines. To get a third line that is coincident, we overlapped the two lines together, first drawing a blue line and then drawing a red line.

Properties of Coincident Lines

• There are infinite common points between the two lines.
• There is no constant space between them.
• The two lines cover each other.
• One line exactly overlaps another line.

Equation of Coincident Line

The following equation can be used to represent linear equations.

y = mx + c

where y is the intercept, m is the slope, and c is the constant.

Consider the general equation

Ax + By = C

Case 1: Suppose that A=2, B=2, C=4 then the above equation becomes

2x + 2y = 4

Case 2: Suppose that A=8, B=8, C=16 then the above equation becomes

8x + 8y = 16

Solving Case 1 and Case 2 equations in that order:

• Case 1 Equation

2x + 2y = 4

x + y = 2

x = 2 – y

y = 2 – x

• Case 2  Equation

8x + 8y = 16

x + y = 2

x = 2 – y

y = 2 – x

In conclusion, we can clearly see that the x and y values of both case 1 and case 2 are equal so both of the equations are coincident.

Equation of Coincident Line Graphically

We have drawn two equation 2x + 2y =4 and 8x + 8y =16. We can see that when x=0:

• Equation 1 becomes 2(0) + 2y =4 simplifying gives y=2
• Equation 2 becomes 8(0) + 8y = 16 simplifying gives y = 2

when y=0:

• Equation 1 becomes 2x + 2(0) = 4 simplifying gives x = 2
• Equation 2 becomes 8x + 8(0) = 16 simplifying gives x = 2

Which clearly shows that these two lines are coincident lines.

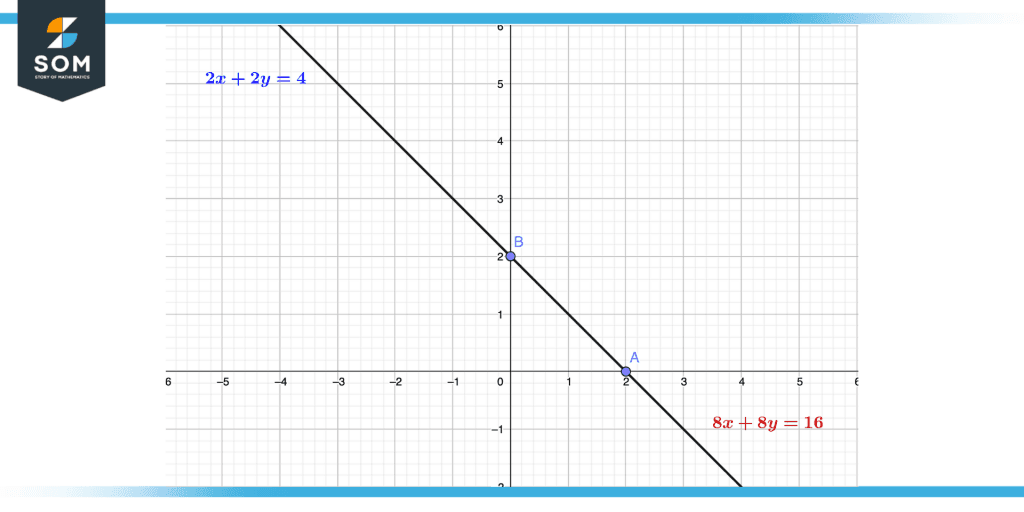
Figure 2 – Graphing coincident lines. The equation in red is four times the equation in blue, so they represent the same line.

Difference Between Coincident Line and Parallel Line

Parallel lines have the same width, whereas coincident lines always intersect each other because parallel lines have a constant space in between them, and they never intersect. A coincidental line is on top of another line and does not have constant space between them; in other words, one line covers the other completely. There are no common points between parallel lines and coincident lines have an infinite number of points shared in common.

The convergence of two lines in Euclidean geometry may be a point, a line, or a vacant set. For instance, PC illustrations, movement planning, and impact location have been used to recognize these cases and observe the convergence point.

Euclidean math call slant lines non-converging lines if they are not in the same plane. When they are on a similar plane, there are three possibilities: assuming that they are alike, they share an unlimited number of focuses; in any case, they have a solitary mark of the crossing point; assuming they are particular and have an identical incline, they should be equal; but if they are particular, they have a similar incline.

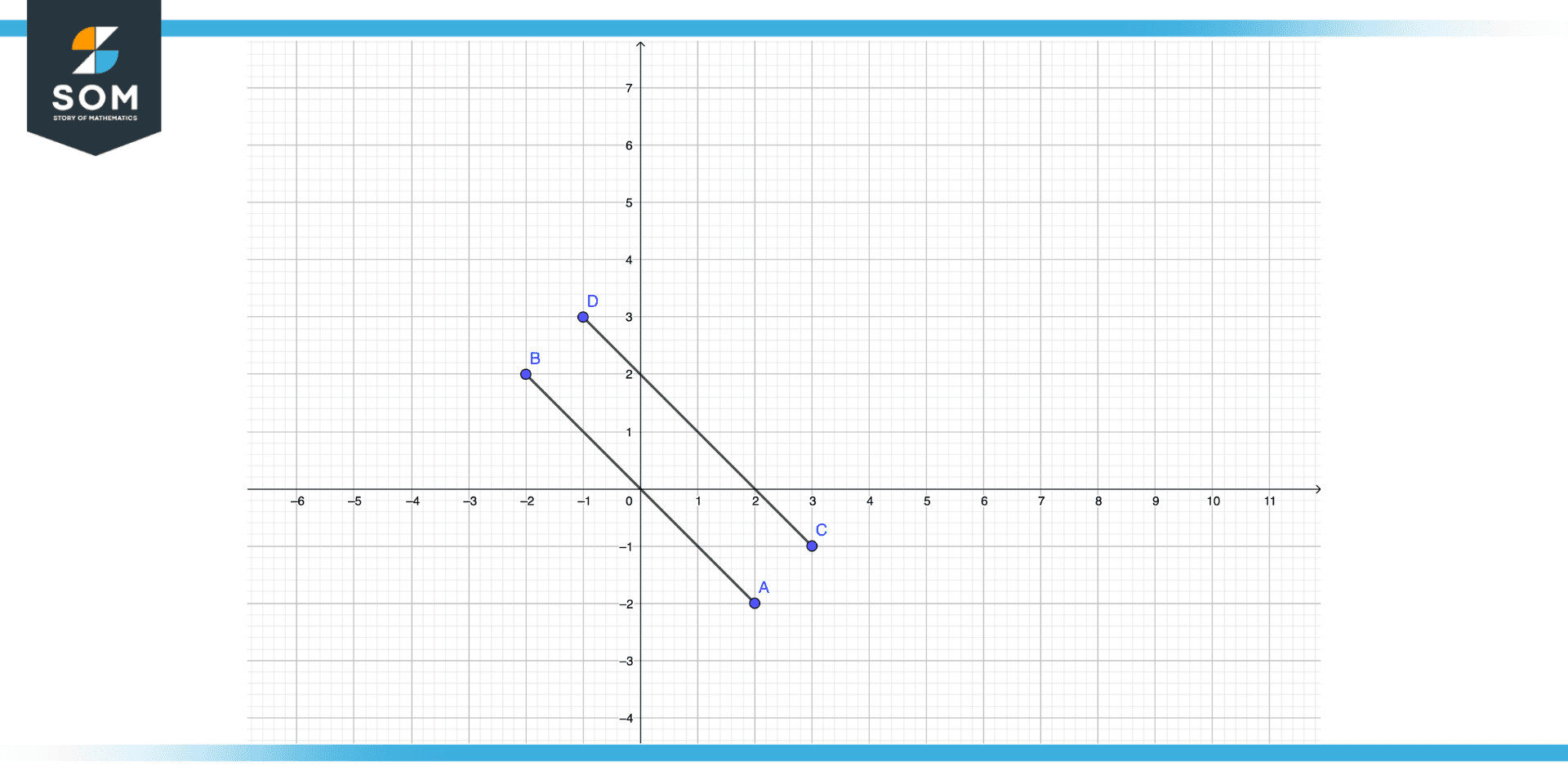
Figure 3 – Parallel lines are not coincident!

Consider the above figure there are no common points between the two lines and there is constant space between them so these lines are referred to as parallel lines.

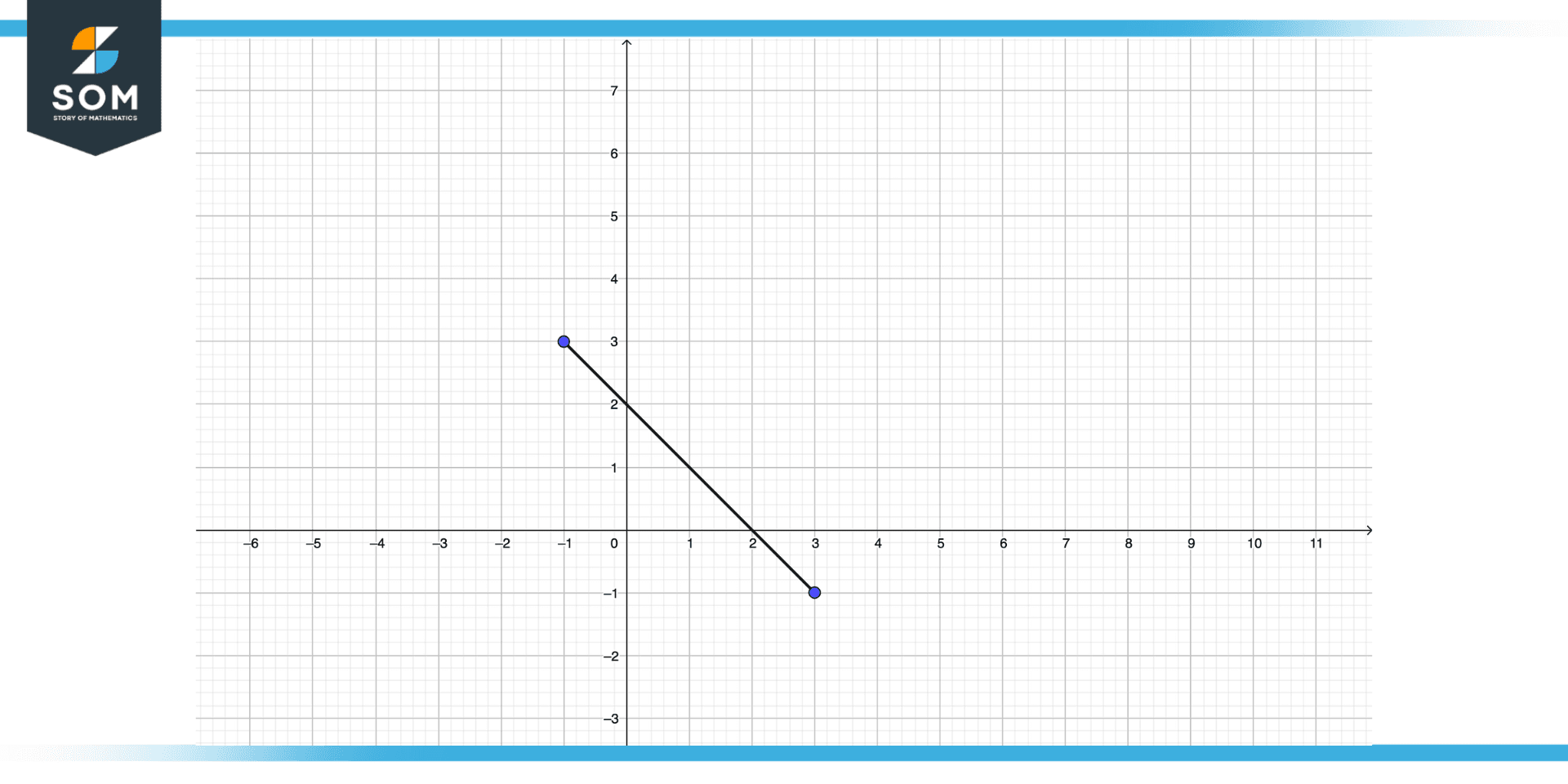
Figure 4 – Coincident lines. It looks like it is just one line, but these are two lines exactly on top of each other!

Consider the above figure there are infinite common points between the two lines moreover there is no constant space between them and they are covering each other so these lines are referred to as coincident lines.

Solved Examples of Coincident Lines

Example 1

Consider the two equations, find whether the equations are coincident or not:

5x + 5y = 10 and 10x + 10y = 20

Solution

Equation 1: 5x + 5y = 10. Put x=0: 

5(0) +5y =10

5y=10

y=2

Put y=0: 

5x +5(0) =10

5x=10

x=2

Equation 2: 10x + 10y = 20. Put x=0: 

10(0) +10y =20

10y=20

y=2

Put y=0: 

10x + 10(0) = 20

10x = 20

x = 2

The x and y values of both equations are the same so they are coincidental lines. Graphically if we plot the two equations we can see that one equation is exactly overlapping another equation and sharing infinite points between each other and also there is no constant space between them.

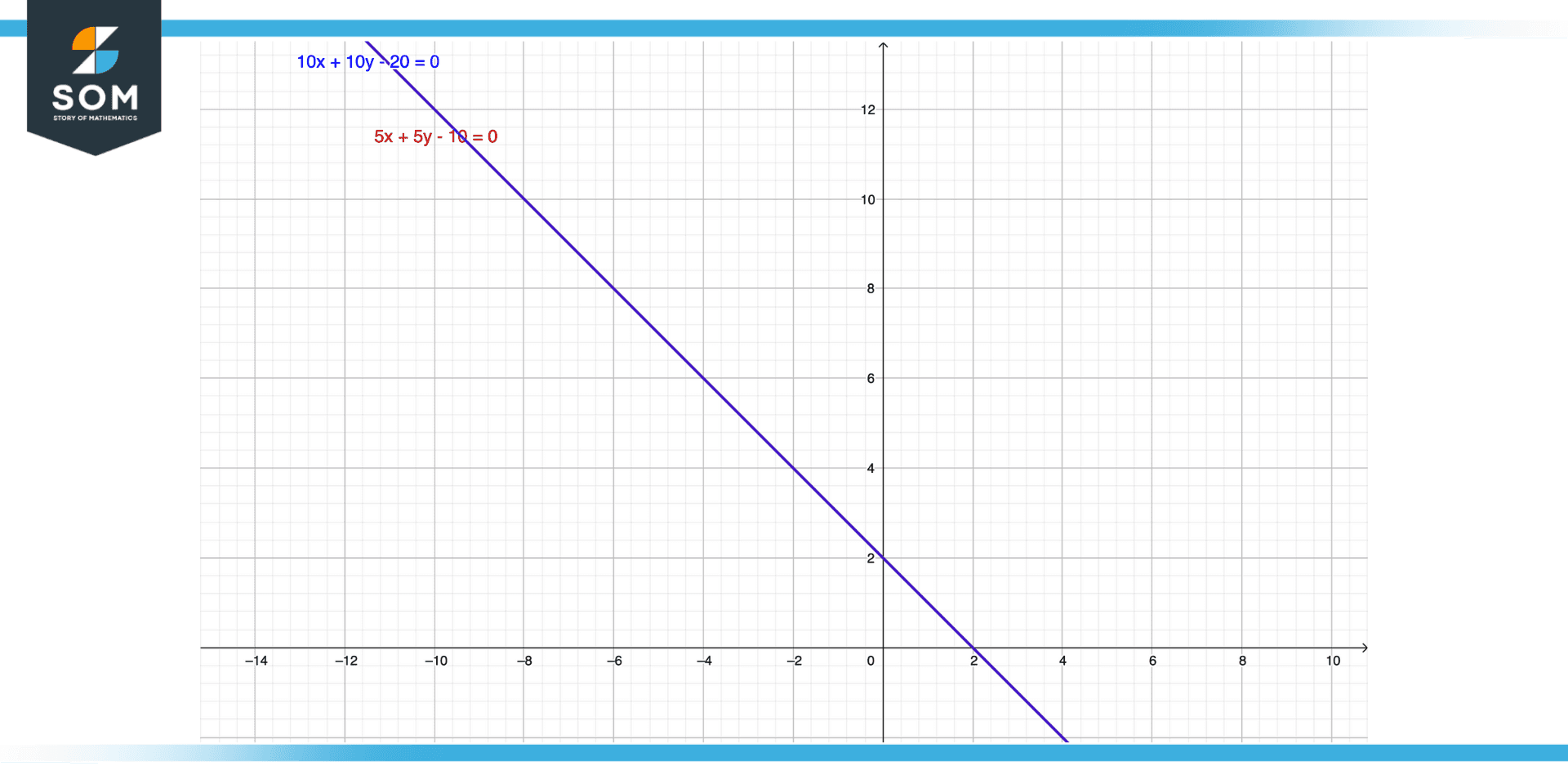
Figure 5 – Example one represents coincident lines, as presented in this graph.

Example 2

Consider the two equations to find whether the line is coincident or not.

Solution

y = 3x + 3 and y = 3x +6

Equation 1: y = 3x + 3. Put x=0:

y=3(0) + 3

y=3

Put y =0:

0=3x+3

x=-1

Equation 1: y = 3x + 6. Put x=0

y=3(0) + 6

y=6

Put y =0

0=3x+6

x=-2

The x and y values of both equations are different so they are not coincident rather they are parallel lines with slope 3 and intercept 2. We can see from the figure below both of the equations are parallel with no common points between them and no intersection along with a constant space between the two lines.

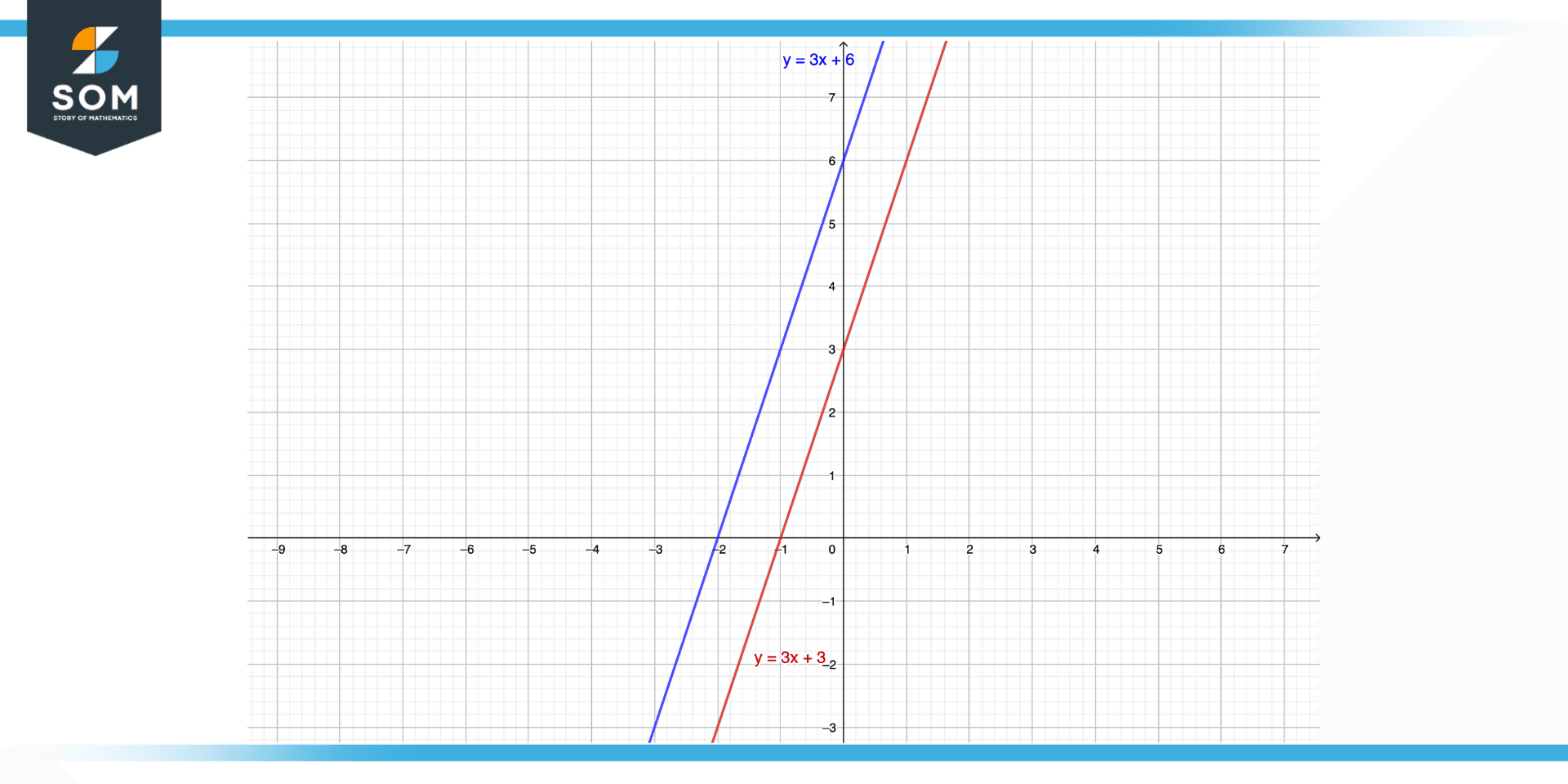
Figure 6 – Example two’s lines as they appear on graph. Notice the lines are parallel, meaning they are not coincident.

Example 3

Consider the two equations to find whether the line is coincident or not:

x+y = 1 and 2x + 2y = 2

Solution

Equation 1: x + y = 1. Put x=0:

0+y=1

y=1

Put y=0:

x+0=1

x=1

Equation 2: 2x + 2y = 2. Put x=0:

2(0)+2y=2

2y=2

y=1

Put y=0:

2x+2(0)=2

2x=2

x=1

The x and y values of both equations are the same so they are coincidental lines. Graphically if we plot the two equations we can see that one equation is exactly overlapping another equation and sharing infinite points between each other and also there is no constant space between them.

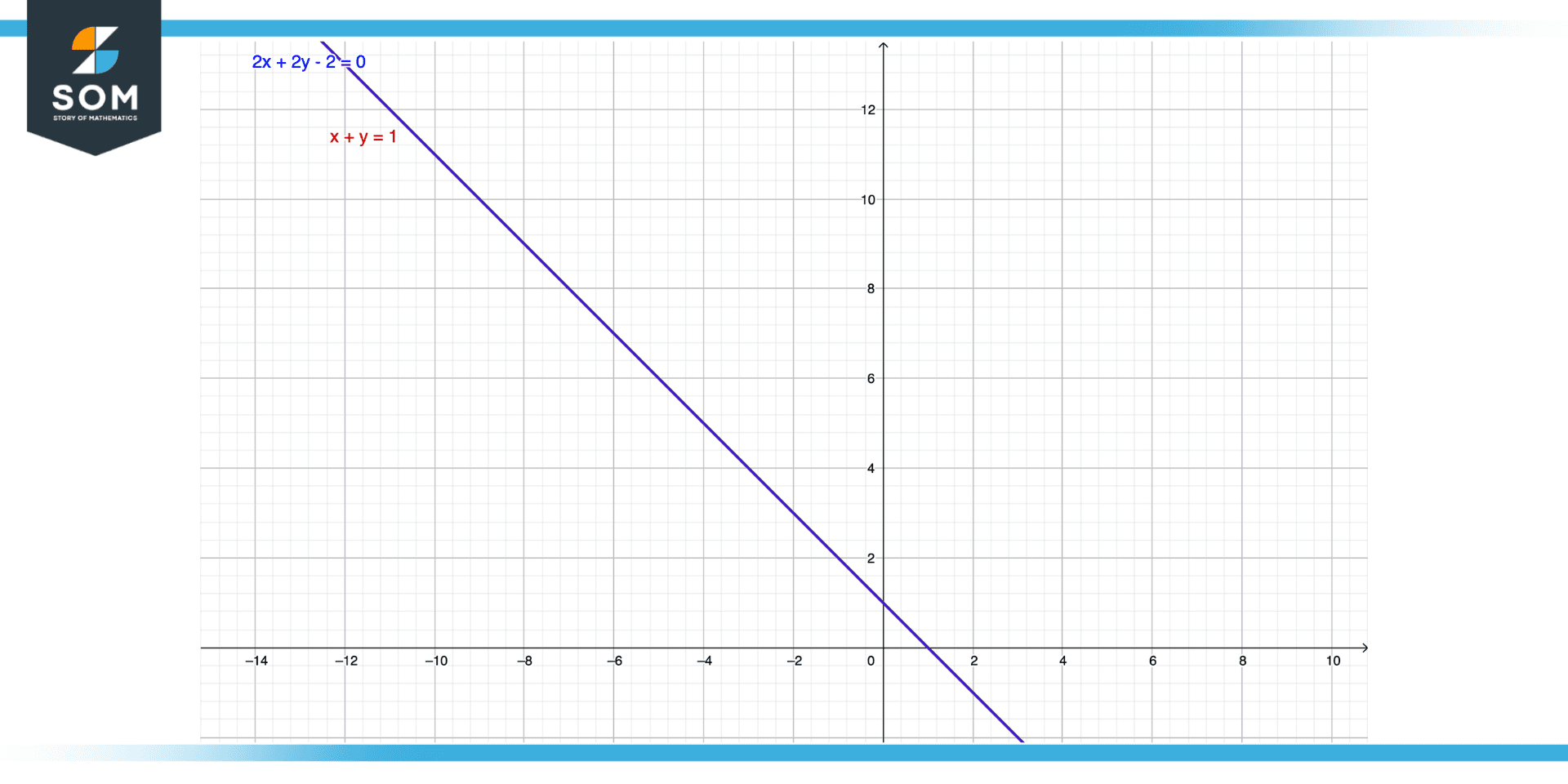
Figure 7 – Graphing the coincident lines in example three

All mathematical drawings and images were created with GeoGebra.

Cluster Definition < Glossary Index > Collinear Definition