JUMP TO TOPIC
Collinear|Definition & Meaning
Definition
Collinearity is a property of points when two or more points passing through or laying on a single or straight line. The word collinear derived from a Latin word “col” meaning together and “linear” meaning same line. The points with these property is called collinear points.
Collinearity in geometry is basically defined as a property of points being on a single and straight line. In a broader sense, the term has been applied to aligned objects or points in a row.
Collinear Points In Maths
A collinear point is a series of two or more points along the same linear fashion. Collinear points are possible on multiple planes however not on multiple lines. Collinearity is the characteristic of points being collinear. So any three or more points are only collinear when they are in the relatively similar straight line. When there is just single line that can cross three different points than that points are considered collinear. Examine the figure below, where the collinear points are A, B, D and E.
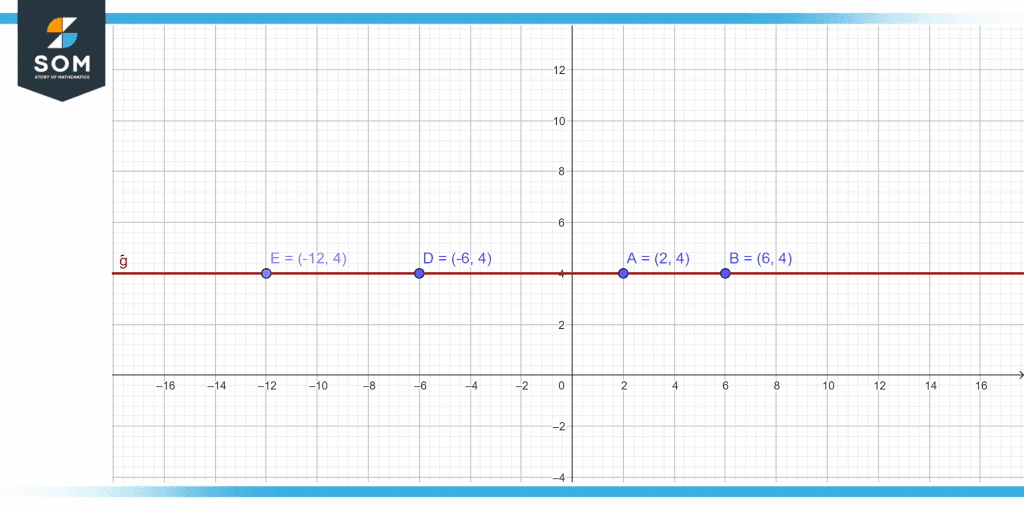
Figure 1 – Four collinear points A,B,D and E
In the above shown figure there are 4 points which are A(2,4), B(6,4), D(-6,4) and E(-12,4) present on a same straight line that is y=4. As these all points are in a row so these points are collinear points.
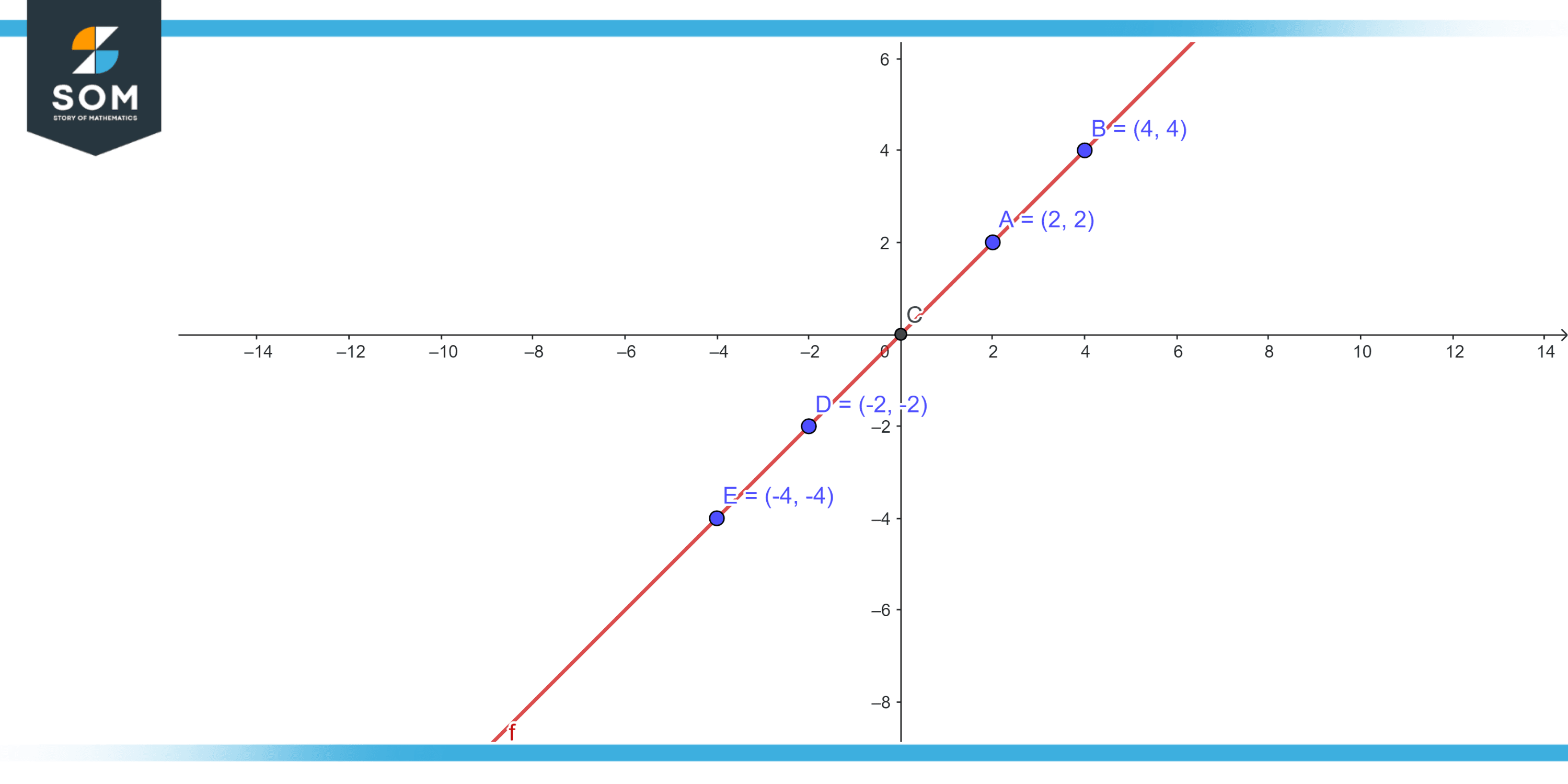
Figure 2 – Collinear points on a line y=x
Above figure is showing different points although the points are different but one thing is same for all these points is that all these points are collinear that is laying on the same straight line y=x.
Real-life Examples
In real life, examples of collinear points include pupils standing in a line during an assembly, parked cars in a straight path in a parking lot, and a set of beads kept in a straight line. Collinear points are useful in solving real-world Euclidean Geometry problems, though many of them are quite complex to discuss here.
In many contexts, collinearity simplifies things. For example, the collinearity between two variables in regression analysis is a particularly helpful fact as it hints at a large correlation between them. Furthermore, the collinearity of calibration points is an important assumption in the process of camera calibration, where the perspective effect of cameras is guessed after a basic linear model based on collinearity.
Formulas For Collinear Points
There are various formulas which are used to find the the collinearity between different points. But the three main formulas used to determine the collinear points are:
- Distance formula
- Area of triangle
- Slope Formula
Distance Formula
We use the distance formula to calculate the distance between the first point and the second point, further the distance in between the second point and third points. Then we check if the sum of these distances are equal with the distance between the first point and the third points. This can only happen if the three points are collinear. The distance formula is utilized to determine the distance between two points for whom coordinates are known to us.
The distance between two points R(x1,y1) and S(x2,y2) can be determine as follow
d = $\mathsf{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}$
Area of Triangle
If three points are collinear, no triangle can be formed. We will check the triangle’s points by inserting them in the triangle area formula. If the area of a triangle is equal to zero, the points are considered collinear. In other term, the triangle made up of three collinear points has no area because it is simply a line connecting the three points. The method for the area of a triangle, which is used to check point collinearity of three points X(x1,y1) ,Y(x2,y2) and Z(x3,y3), is as follows:
Area = $\mathsf{\dfrac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]}$= 0
Slope Formula
We use the slope formula to calculate the slope of the lines formed by the three points under consideration. If the slopes of the three points are equal, then the three points seems to be collinear.
For instance, if we have three points A, B, and C, these points will be collinear if the slope of line AB equals the slope of line BC which is further equals to the slope of a line AC. This slope formula is considered when there is need to find the slope of a line connecting two points.
The formula of the slope joining two points is given by the following equation:
Slope = m = (y2 – y1) / (x2 – x1)
Example Problems on Checking Collinearity of Points
Example 1
Find if these points A(−3,−1), B(−1,0), and C(1,1) are collinear.
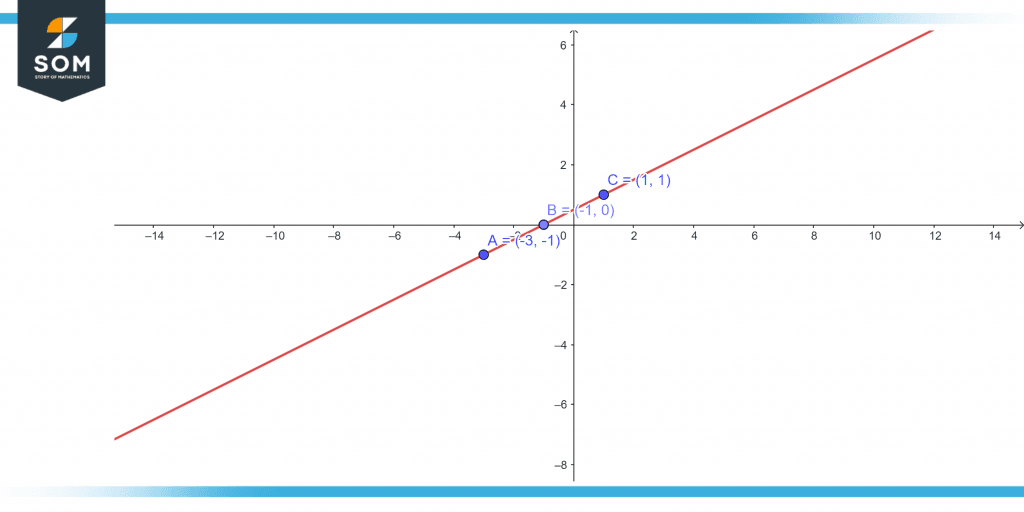
Figure 3 – Three collinear points
Solution
These three points will be considered as collinear if the addition of distances between AB and BC is equal to distance between CA.
Distance between AB = $\mathsf{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}$
= $\mathsf{\sqrt{(-1+3)^2 + (0+1)^2}}$
= $\mathsf{\sqrt{5}}$
Distance between BC = $\mathsf{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}$
= $\mathsf{\sqrt{(1+1)^2 + (1-0)^2}}$
= $\mathsf{\sqrt{5}}$
Distance between CA = $\mathsf{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}$
= $\mathsf{\sqrt{(1+3)^2 + (1+1)^2}}$
= $\mathsf{\sqrt{20}}$
= 2 $\mathsf{\sqrt{5}}$
To check collinearity,
= $\mathsf{\sqrt{5} + \sqrt{5} = 2\sqrt{5}}$
So point A,B and C are collinear.
Example 2
Find if the following points P(-1.5,3), Q(6,-2) and R(-3,4) of a triangle are collinear?
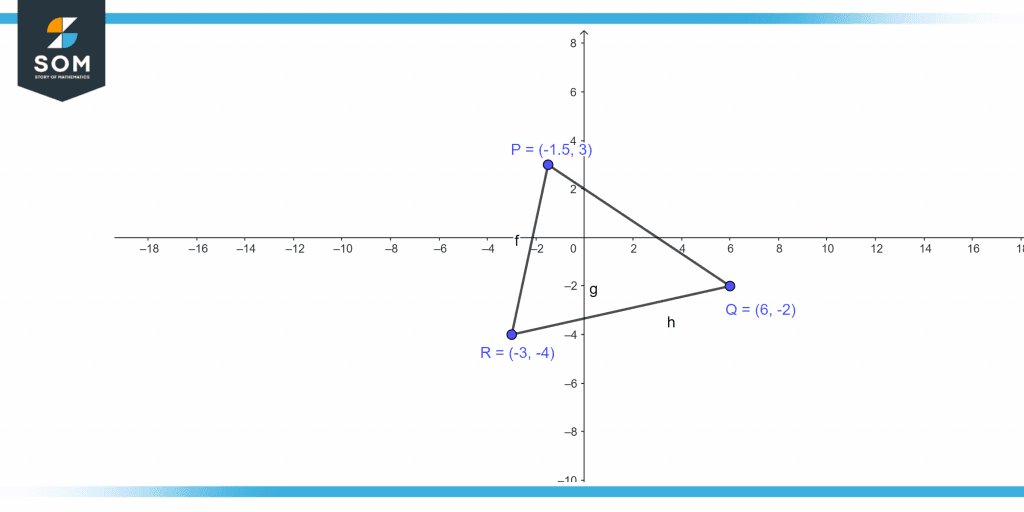
Figure 4 – Collinear points on triangle
Solution
Area of Triangle PQR = $\mathsf{\dfrac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]}$
= $\mathsf{\dfrac{1}{2}}$[-1.5(-2-4)+6(4-3)-3(3-(-2)]
= $\mathsf{\dfrac{1}{2}}$[-1.5(-6)+6(1)-3(3+2)]
= $\mathsf{\dfrac{1}{2}}$[-1.5(-6)+6-3(5)]
= $\mathsf{\dfrac{1}{2}}$[9+6-15]
= $\mathsf{\dfrac{1}{2}}$[0]
= 0
Since the area is zero here so the vertices are collinear.
Example 3
Show if the following three points x(1, 3), Y(5, 7) and Z(9, 11) are collinear points?
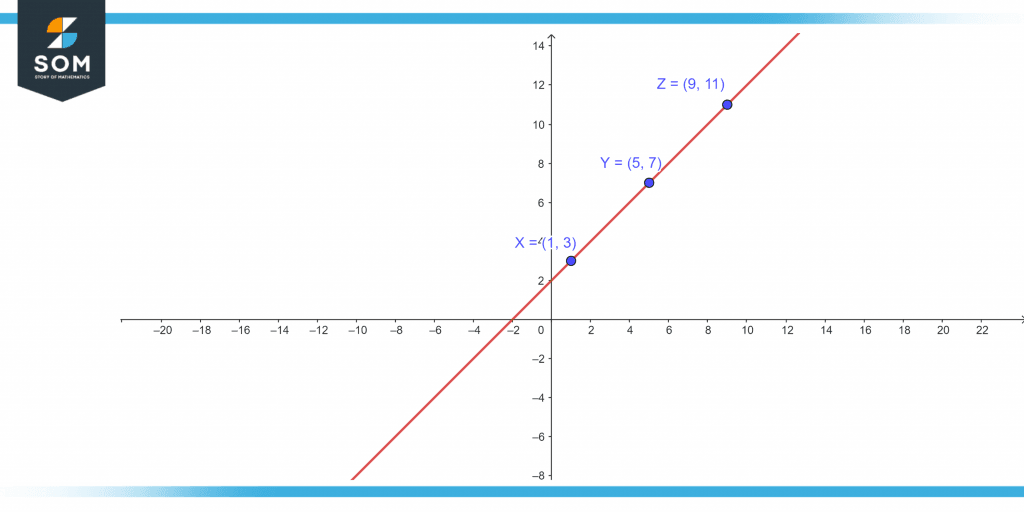
Figure 5 – Slope of collinear points
Solution
If these three points X(1, 3), Y(5, 7) and Z(9, 11) are really collinear, then the slopes of any two given points, XY, YZ & XZ will be equal.
Now, by using the above slope formula we can find the slopes of the given points,
Slope of XY = (7 – 3)/ (5 – 1) = 4/4 = 1
Slope of YZ = (11 – 7)/ (9 – 5) = 2/2 = 1
Slope of XZ = (11 – 3) /(9 – 1) = 8/8 = 1
From the above calculations, we can clearly see that the slopes of points XY, YZ, and XZ are the same (that is, 1) for all given points, which means that all these three points are collinear.
All the figures above were created with Geogebra.
