Combination|Definition & Meaning

The figure below is a fairly simple illustration of the concept of combinations in Mathematics. 

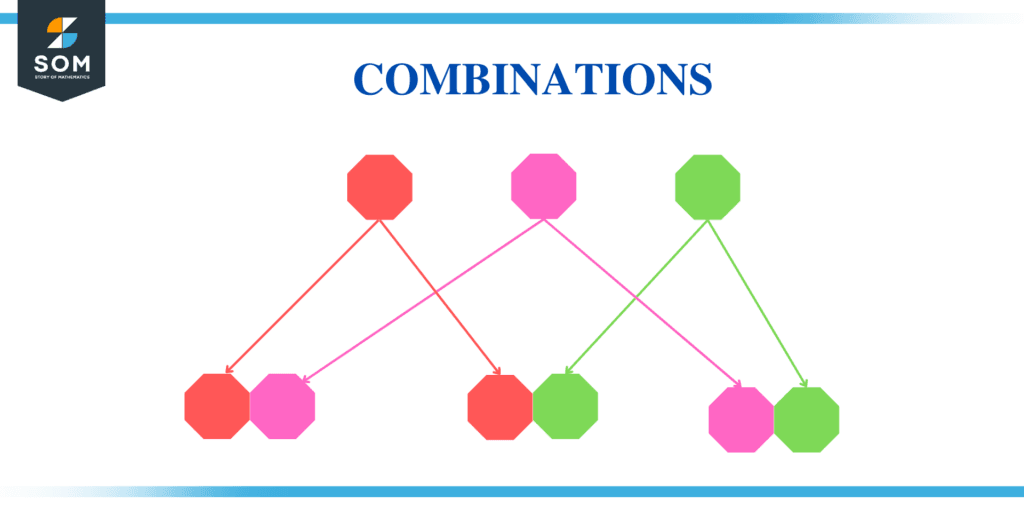
Figure 1: Illustration of Combinations

We frequently encounter circumstances in daily life where we have to choose certain items from a group. Mostly, we are not concerned about ordering the objects at all; rather, we are only concerned with selecting a certain number of items out of a total number of items. A combination is selecting some or all of several distinct items, where the sequence in which the elements are selected is irrelevant.

People often mix up Combinations with permutations. However, when it comes to permutations, the order in which the things are chosen is quite important. For instance, when it comes to combinations, the arrangement of “ab” and “ba” are the same since they are believed to be the same arrangement. However, when looking at permutations, the arrangement of “ab” and “ba” are not the same.

For example, in the diagram below, we can see the comparison between permutation and combination of three objects, “A,” “B,” and “C.” We can observe that the maximum number of arrangements in the case of permutations is six, whereas, in the case of combination, the maximum number of arrangements is three.

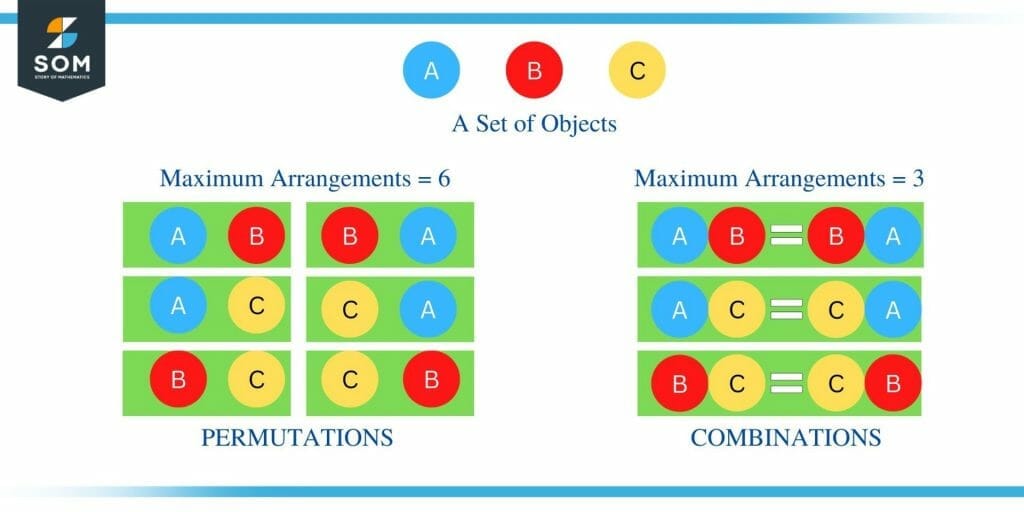
Figure 2: Permutations vs. Combinations

Formula of Combinations

“ⁿC_k” is the formula that is most commonly referred to as the counting formula. This is because it can be utilised to determine the total number of potential combinations that exist inside a particular scenario. In a general sense, the number of distinct combinations that are conceivable is symbolized by the notation “ⁿC_k.” This is the case when there are “n” number of objects, and one is to choose “k” from among these. The number of possible subset combinations can be determined using the notation ⁿC_k, which can be interpreted as “n choose k.” It is self-evident that the number of subsets must be divided by k!, given that k! arrangements will be present for each possible selection of k items, as this is the only logical way to proceed. Therefore,

ⁿC_k = C (n, k) = $\dfrac{n!}{k!\left(n-k\right)!}$

The formula is explained in the following figure.

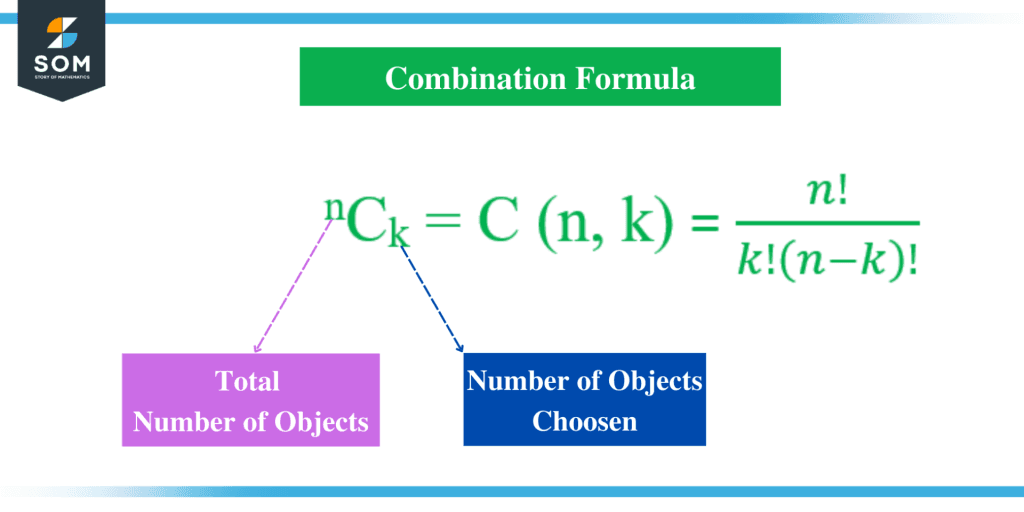
Figure 3: Combination Formula Explained

Furthermore, you need to be familiar with factorial calculations in order to calculate combinations. The multiple of all positive integers that are greater than zero and are less than the number whose factorial you are calculating is known as a factorial. An exclamation point is written after the number to represent a factorial. For instance, you would type 5! to represent the factorial of 5. Now in order to find the factorial of 5, you should multiply all positive integers that are both greater than zero and are less than 5, as shown below:

5! = 5 x 4 x 3 x 2 x 1

After multiplying the above numbers with each other, we found that factorial of 5 is equal to 720. Now let us take another example of factorial by writing and estimating the factorial of 9. As we have already discussed that an exclamation point is written after the number to represent a factorial. So, the factorial of 9 would be expressed as “9!”. Now it can be calculated as shown below

9! = 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

9! = 362880

Applications of Combinations

Combinations are not only studied in the field of combinatorics but they are also utilised in a variety of other fields, such as mathematics and finance. Some of the real examples are discussed below

• Locking Systems are one of the most common examples of combinations. In combination locks, a combination of a usually three or four-digit key opens or closes the lock.
• Computer Architectures also involve the use of combinations.
• Data encryption, a key feature of modern-day security systems, also involves the usage of combinations.
• Concept of combinations is also employed in the field of pattern analysis.

Examples of Finding Possible Combinations

Example 1

Three table tennis players, A, B, and C, were shortlisted by the sports board to participate in the tournament. Out of these three players, a team of two players has to be selected. Find out how many ways we can form a team.

Solution

As we have discussed above, when it comes to combination problems, the order in which the team has to be selected or formed is not important. Such that,

AB = BA, BC = CB, and similarly AC = CA.

Therefore, we can form the team in three ways.

Since we know that the combination formula is:

ⁿC_k = C (n, k) = $\dfrac{n!}{k!\left(n-k\right)!}$

Now, Apply the formula in the above problem,

³C₂= C (3, 2) = $\dfrac{3!}{2!\left(3-2\right)!}$

³C₂ =$\dfrac{(3\ \times\ 2\ \times\ 1)}{(2\ \times\ 1\ \times\ 1)}$

³C₂ = 3

This is also illustrated in the figure below.

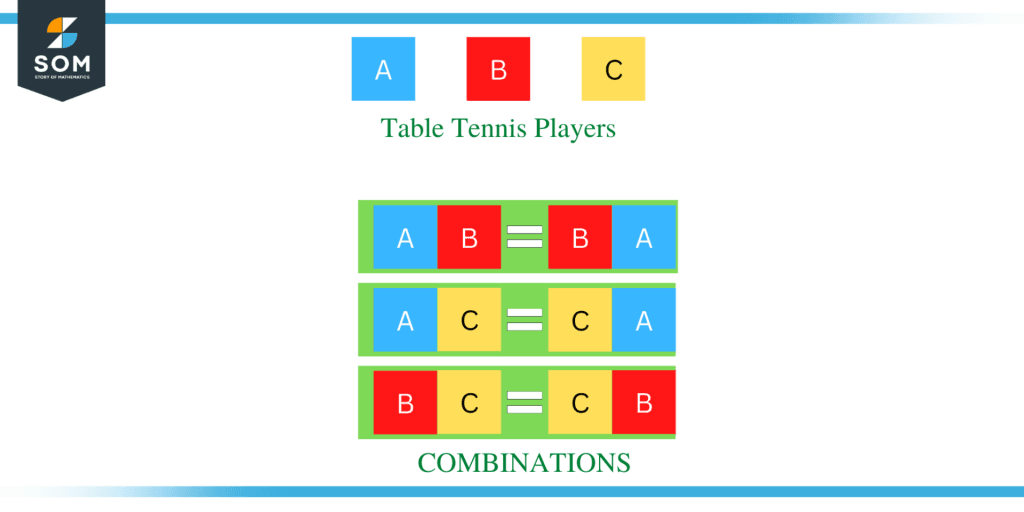
Figure 4: Illustration of Example 1.

Example 2

Frank decided to spend his vacations visiting as many US States as possible. After considering his time and budget, he discovered that he could visit only six of the total fifty US States. He is not concerned about the order in which he visits them as well as the complexity of the combination. Find out how many different combinations of states John can visit.

Solution

As mentioned in the problem, the order of the visit is not something john is concerned about. So, the problem at hand is pretty simple. Six states, in no particular order, have to be selected out of the 50 US states.

Now, we know that the combination formula is:

ⁿC_k = C (n, k) = $\dfrac{n!}{k!\left(n-k\right)!}$

⁵⁰C₆ = C (50, 6) = $\dfrac{50!}{6!\left(50-6\right)!}$

⁵⁰C₆ = C (50, 6) = $\dfrac{50!}{6!\ \times\ 44!}$

⁵⁰C₆ = C (50, 6) = $\dfrac{(50\ \times\ 49\ \times\ \times\ 48\ \times\ 47\ \times\ 46\ \times\ 45)}{(6\ \times\ 5\ \times\ 4\ \times\ 3\ \times\ 2\ \times\ 1)}$

⁵⁰C₆ = C (50, 6) = $\dfrac{11441304000}{720}$

⁵⁰C₆ = 15, 890, 700

All images/mathematical drawings were created with GeoGebra.

Column Graph Definition < Glossary Index > Commission Definition