Common Difference|Definition & Meaning

Sequences and the Arithmetic Sequence 

A set of numerals placed in a definite order is known as a sequence. For example, 1,3,6,10,15 is a sequence.

There are many types of sequences but the arithmetic sequence deals with the concept of common difference. To understand the common difference, one must know about the arithmetic sequence.

An Arithmetic Sequence or progression is an ordered sequence arranged with a common difference between its two consecutive terms.

Positive Common Difference

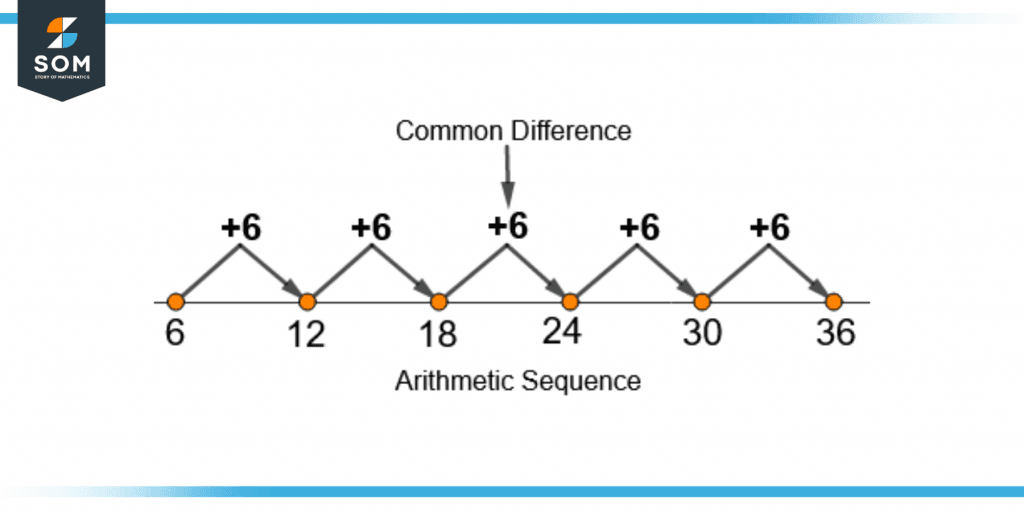
Figure 1 – Arithmetic Sequence With A Positive Common Difference

An arithmetic sequence with a positive common difference is shown in figure 1. It has the first term as 6, the second as 12, and so on. The common difference d for this sequence is +6.

Negative Common Difference

The arithmetic sequence shown in figure 2 has a negative common difference of -4. Note that the terms of the arithmetic sequence are in descending order.

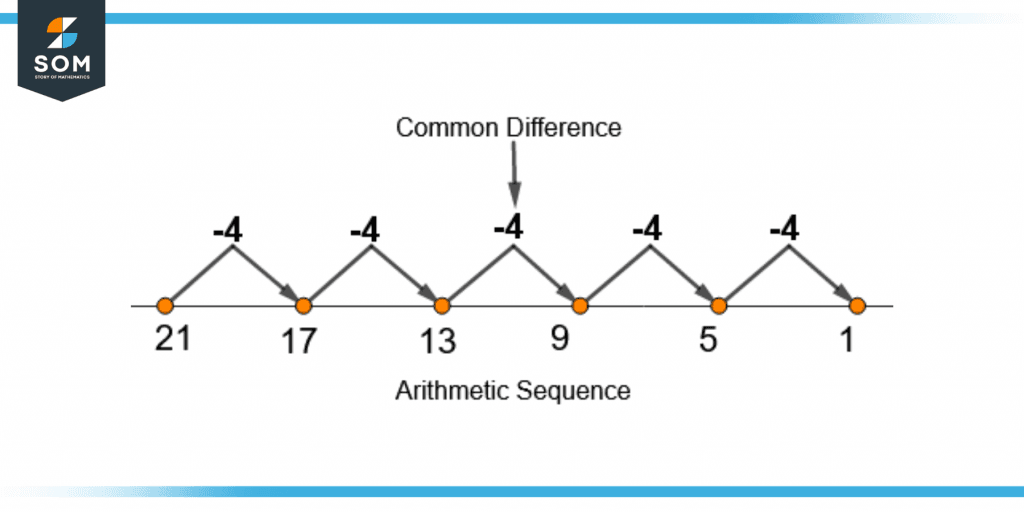
Figure 2 – Arithmetic Sequence With A Negative Common Difference

Common Difference of a Finite and Infinite Arithmetic Sequence

The arithmetic sequence can be finite or infinite. For example, the arithmetic sequence 3, 7, 11, 15, 19 is finite as it has an ending term of 19. It has a finite number of terms.

On the other hand, the arithmetic sequence 3,6,9,12,… is an infinite sequence as the dots indicate that the terms will go to infinity.

Figure 3 shows a finite and an infinite arithmetic sequence. Both have a common difference of +2.

Figure 3 – Finite And Infinite Arithmetic Sequences

Importance of Common Differences

Common difference plays an essential role in an arithmetic sequence. Without a common difference, the sequence won’t even be arithmetic!

Also, it plays a crucial role in finding the next term or any term of the arithmetic sequence.

Finding the mth Term of an Arithmetic Sequence

An arithmetic sequence consists of many terms. The following steps are required to find the mth term of an arithmetic sequence.

Knowing the First Term

Knowing the first term is essential for computing any arithmetic term. For example, the first term in the arithmetic sequence 6, 10, 14, 18 is 6. It is denoted by $b_{1}$.

Knowing the Common Difference

The common difference d can be calculated by subtracting the second term from the first term. The value of d would be the same by subtracting the third term from the second term.

The mathematical formula for common difference can be generalized as follows:

d = $b_{m+1}$ – $b_{m}$

Where $b_{m+1}$ is the term next to $b_{m}$.

Without knowing the common difference, the mth term cannot be found.

Similarly, the next term $b_{m+1}$ can be calculated if the previous term b_{m} and the common difference d are known. The formula becomes:

$b_{m+1}$ = $b_{m}$ + d

Calculating the mth Term

The following mathematical formula is used to find the mth term of the arithmetic sequence.

$b_{m}$ = $b_{1}$ + ( m – 1 ).d

Here, $b_{m}$ represents the mth term. The m indicates the position of the term in the sequence.

For example, the tenth term is required in the sequence 6, 10, 14, 18 so the value of m will be 10. The first term $b_{1}$ of the sequence is 6.

The common difference can be calculated as follows:

d = $b_{m+1}$ – $b_{m}$

d = $b_{2}$ – $b_{1}$

d = 10 – 6

d = 4

By putting the values of $b_{1}$, m, and d, the tenth term of the sequence is calculated as follows:

$b_{10}$ = 6 + ( 10 – 1 )4

$b_{10}$ = 6 + ( 9 )4

$b_{10}$ = 6 + 36

$b_{10}$ = 42

The mth term can also be calculated by only knowing the common difference.

In the above sequence, 6, 10, 14, 18 the common difference 4 is added till the tenth position of the sequence to find the tenth term. It is shown in figure 4.

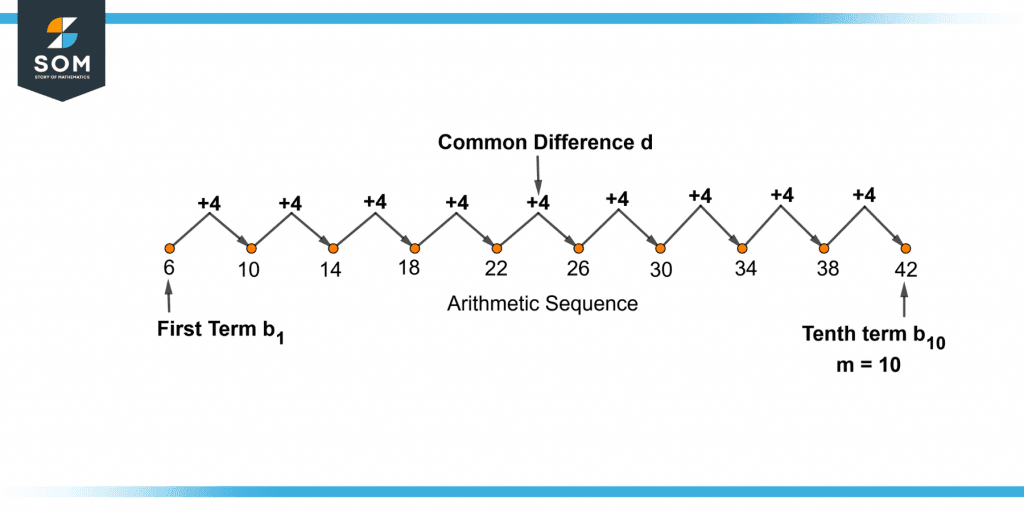
Figure 4 – Finding the mth Term Using the Common Difference

Example of Finding the Common Difference in an Arithmetic Sequence

Which of the following sequences is arithmetic? If arithmetic, which has a positive or a negative common difference?

a) 22, 19, 16, 13, 10, 7

b) 30, 34, 38, 42, 46, 50

c) 2, 4, 7, 9, 12

d) 4, 8, 16, 32, 64

Solution

(a) 22, 19, 16, 13, 10, 7

First, the difference between the first term and the second term needs to be calculated. It is

$d_{1}$ = $b_{2}$ – $b_{1}$ = 19 – 22 = -3

Next, the difference between the second and the third term is calculated.

$d_{2}$ = $b_{3}$ – $b_{2}$ = 16 – 19 = -3

As $d_{1}$ is equal to $d_{2}$, the sequence is arithmetic with a negative common difference of d = -3.

(b) 30, 34, 38, 42, 46, 50

The first term is subtracted from the second term to find the difference $d_{1}$ as follows:

$d_{1}$ = $b_{2}$ – $b_{1}$ = 34 – 30 = +4

To check whether this difference is common, the second term is subtracted from the third term as follows:

$d_{2}$ = $b_{3}$ – $b_{2}$ = 38 – 34 = 4

As $d_{1}$ and $d_{2}$ are the same, the sequence has a positive common difference of +4. Hence, the sequence is arithmetic.

(c) 2, 4, 7, 9, 12

Calculating $d_{1}$ and $d_{2}$ to as follows:

$d_{1}$ = $b_{2}$ – $b_{1}$ = 4 – 2 = +2

$d_{2}$ = $b_{3}$ – $b_{2}$ = 7 – 4 = +3

As $d_{1}$ is not equal to $d_{2}$, there is no common difference in the sequence. The sequence is not arithmetic.

(d) 4, 8, 16, 32, 64

Subtracting the first from the second term gives 8 – 4 = 4. Also, the subtracting the second from the third term gives 16 – 8 = 8.

Both the differences are not equal, hence the sequence is not arithmetic.

The given sequence does have a common ratio r which is 2. It means that the first term 4 is multiplied by 2 to get the second term 8.

Similarly, the third term is obtained by multiplying the second term by 2. So, the sequence is geometric.

All the images are created using GeoGebra.

Commission Definition < Glossary Index > Common Factor Definition