JUMP TO TOPIC
Common Factor|Definition & Meaning
Definition
When we write out the factors of at least two numbers, any factors that appear in the list of factors of both numbers are called common factors, and we say the two numbers “share” these factors. For example, 4 has factors 1,2, and 4, while 10 has factors 1,2,5, and 10. Factors 1 and 2 appear in both numbers’ factors lists so they are the common factor of 4.
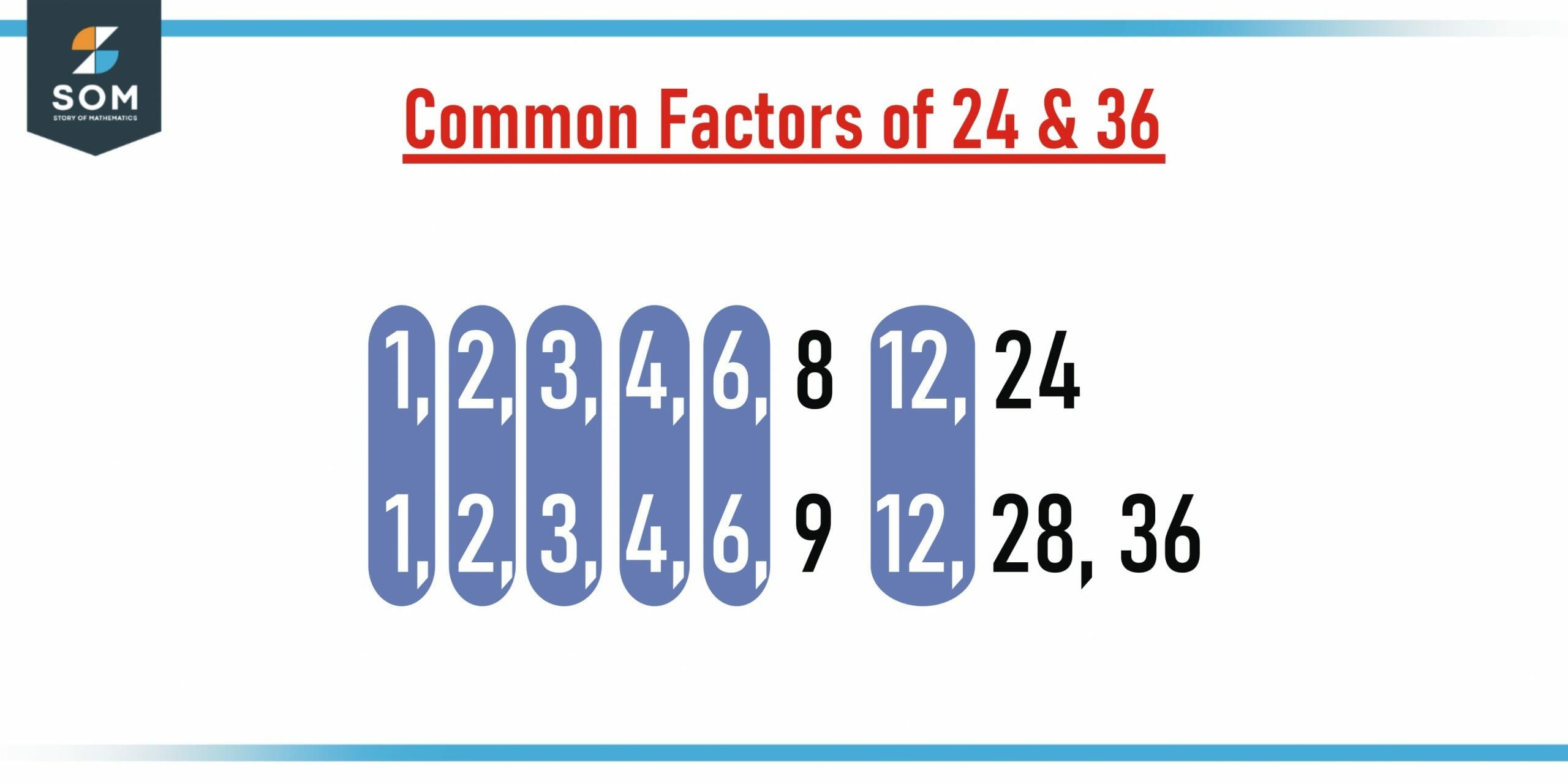
Figure 1 – Common Factors of 24 and 36
In maths, Common factors are defined as “the result of two or more numbers being divided by the same number(s), known as common divisors of those numbers. Another way to describe a common factor is to state that it is a number that divides two or more numbers equally with no remainder left.
Two Numbers With Common Factors
The easiest way to find the common factors between two numbers is to list each factor separately and then compare them together to find a common factor. Then write the factors that both numbers have in common. It is known as the common factor of two given numbers.
Finding Common Factors
A factor is a number that completely divides the original number. To determine if two or more numbers have a common factor, follow the steps below.
- Calculate the factors of each number.
- Identify the common factors (those that appear in the factor list of all the original numbers).
Let us take an example. Find out the factors that are common to both 8 and 32:
8 = 1, 2, 4, 8
32 = 1, 2, 4, 8, 16
Here we can see that both 8 and 32 have 1, 2, 4, and 8 as common factors.
Greatest Common Factor
It is the largest common factor between two or more numbers that we call GCF-Greatest Common Factor. To determine which two or more numbers, have a few factors in common, we will have to take out all the factors that are common to the two or more numbers and write them down. Among the common factors, the greatest common factor is the largest number.
Consider the natural numbers p and q. GCF is the number that divides two natural numbers (p, q), and that number is the largest number that can be used to divide p and q.
Another name for it is the greatest common factor, the greatest common divisor, and the highest common factor. List the factors of two or more numbers and you can find the HCF of those numbers.
The prime factorization method can be used for larger numbers to reduce their complexity. Prime factorization refers to the method of expressing a number in terms of its prime factors.
Finding HCF By Listing
- Give a brief description of each number’s factors.
- Find the greatest number of items that are common to both lists by comparing them.
Let us take an example. Find the HCF of 15 and 33:
Factors of 15= 1, 3, 5
Factors of 33= 1, 3, 11, 33
HCF of 15 and 33 is 3.
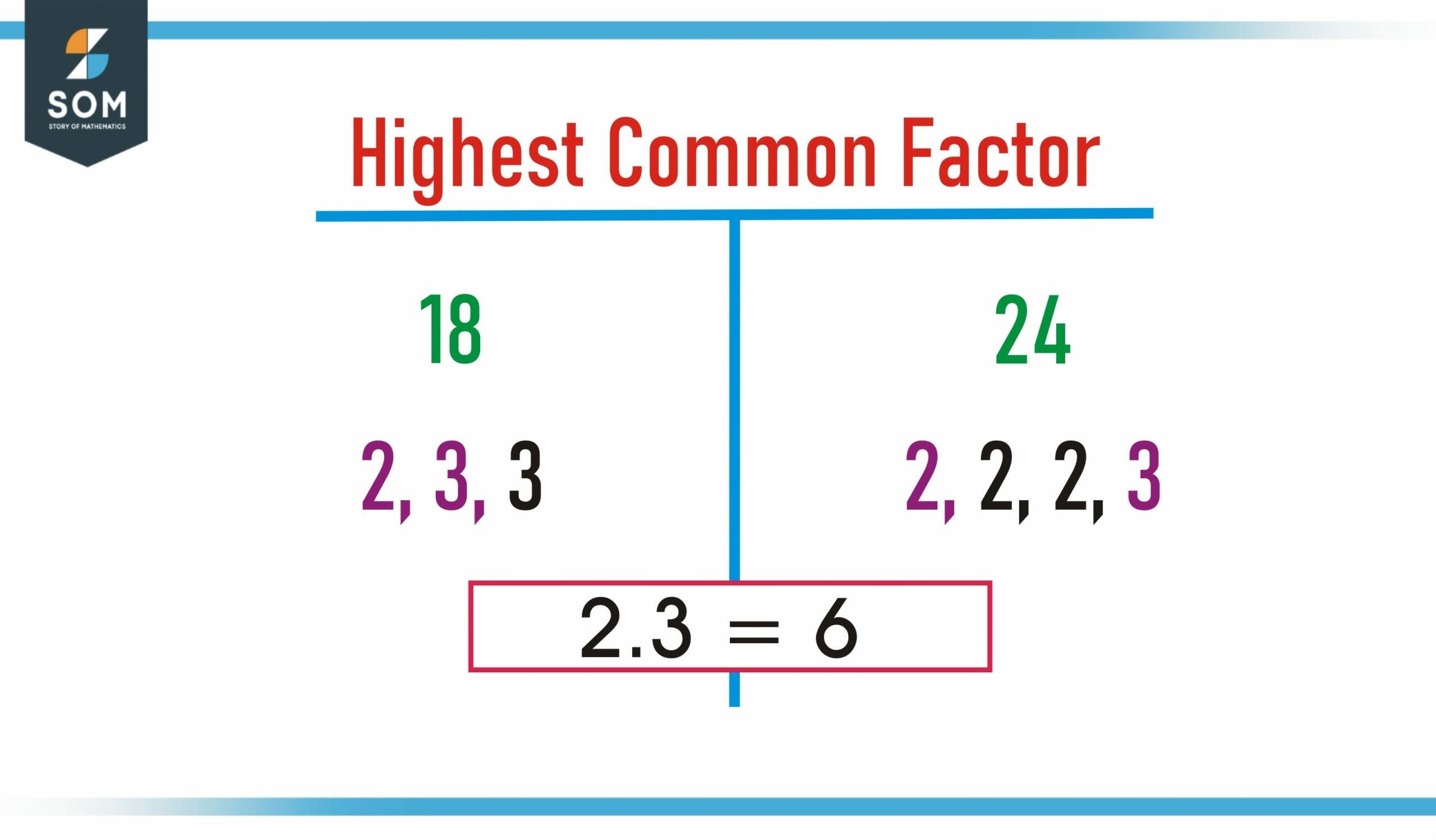
Figure 2 – Highest Common Factor of 18 and 24
Finding HCF by Prime Factorization
The HCF or GCF of two numbers can be found with the following steps:
- For each number, draw a factor tree. A factor tree may need to be reviewed.
- The numbers should be written in terms of the products of their prime factors. If the index form is not used, it can be easier to handle the data.
- Determine whether each product of prime factors contains a common prime factor.
- Multiply the prime factors together to find the HCF.
This is a fairly tough method that should be studied separately.
Least Common Multiple
‘Least Common Multiple’ is the abbreviation for LCM. LCM is the term used to indicate that the lowest possible number that can be divided by both numbers is the least common multiple (LCM). Listing of two or more numbers can be done so that it is possible to find their lowest common multiple (LCM) by comparing them. Prime factorization is useful for larger numbers.
Finding LCM by Listing
- Each number should be multiplied by consecutive multiples.
- Every list contains the LCM as the first multiple.
As an example, consider finding the LCM of 16 and 44. First, we list out a few multiples of the two numbers:
Multiples of 6 = 48, 42, 36, 30, 24, 18, 12, 6
Multiples of 8 = 48, 40, 32, 24, 16, 8
Normally, you would continue listing consecutive multiples of 50 and 10 until you find a matching number. So here, the LCM is 24 (48 is also common, but 24 is the smallest shared multiple).
Finding LCM by Factorization
The process can be explained step-by-step as follows:
- For each number, draw a factor tree.
- Calculate the prime factor of each number. By not using index forms, it can be easier.
- In each of the prime factor products, identify the common prime factors.
- For each number, there are unique prime factors that do not apply to all products.
- Using the common factors of two numbers, you can find the LCM by multiplying the common factors with the unique factors of the two numbers.
This is generally a better way of finding the LCM as compared to the brute force method of first finding the multiples and then searching for shared ones.
Common Factor Applications
When simplifying fractions, common factors are useful. The fraction can be reduced to its simplest form if there is a common factor between the numerator and denominator. Time-work problems and price comparison are other applications of this topic. Identifying the GCF and factoring is one of the most common math skills that we use in our daily lives.
Examples of Common Factors
Example 1
Calculate the GCF of 20 and 44.

Figure 3 – GCF of 18 and 24
Solution
Let us first see what the factors are of 20 and 44, and then we will see what the factors are common to both of these.
Factors of 44 = 44, 22, 11, 4, 2, and 1
Factors of 20 = 20, 10, 5, 4, 2, and 1
The common factors between 20 and 44 are 1, 2, and 4. 4 is the greatest common factor among these numbers. Thus, the GCF of 20 and 44 is 4, which is written as GCF(20, 44) = 4
Example 2
Find out the common factors of 12, 32, and 46.
Solution
Factors of 32 = 32, 16, 8, 4, 2, 1
Factors of 12 = 12, 6, 4, 3, 2, 1
Factors of 46 = 46, 23, 2, 1
The common factors here are 1 and 2.
Example 3
Determine the LCM of 12 and 6.
Solution
Multiple of 6 = 1, 3, 6
Multiple of 12 = 1, 2, 3
The LCM 6 and 12 other than 1 is 3.
All mathematical images are generated using GeoGebra.
