Common Fraction|Definition & Meaning

Sometimes called a vulgar fraction, it is the opposite of a decimal fraction, where one or both the numerator and denominator are decimal numbers (or decimal fractions).  

Understanding Common Fractions With Shapes

We illustrate the concept of common fractions using the following illustrations:

Figure 1 – A whole circle, represented as a fraction 1/1 = 1.

The circle in Figure 1 is whole. We can show it with the common fraction 1/1 = 1 since we have not split it into parts (sectors). 

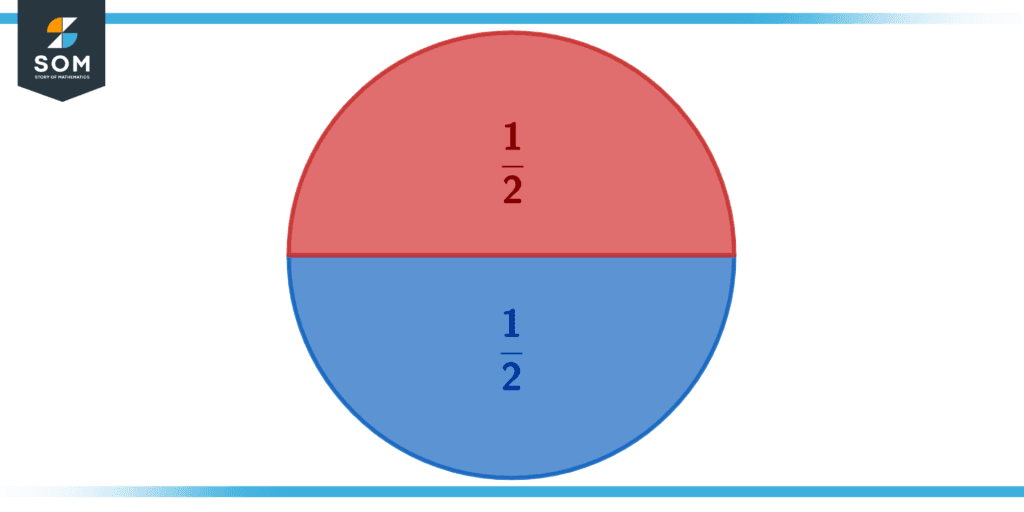
Figure 2 – Circle image divided into two sections showing 1/2 fractions.

When we split a circle into two equal parts, we get two semi-circles as shown in Figure 2. Since each semi-circle is one-half of a circle, we get the common fraction 1/2. Adding up the two parts gets us the full circle as 1/2 + 1/2 = 2/2 = 1.

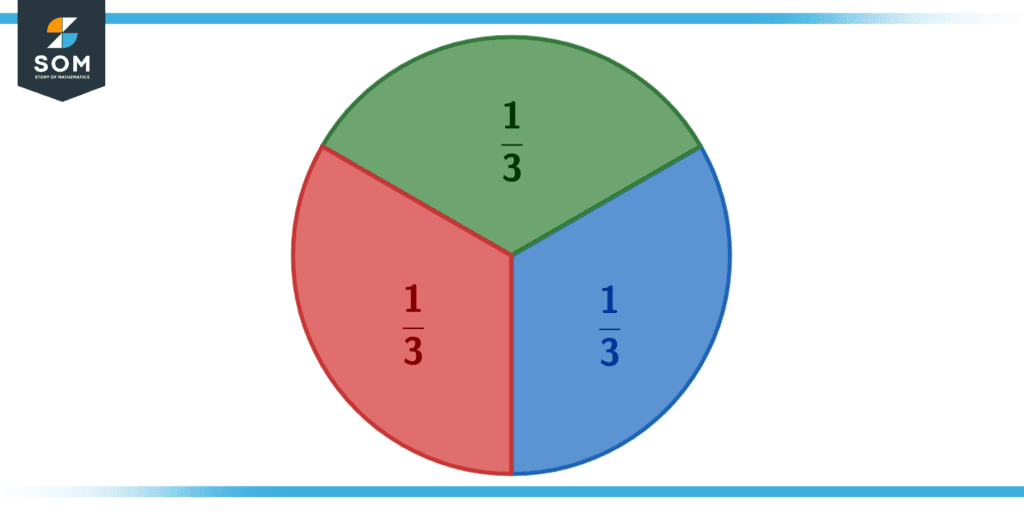
Figure 3 – Circle image divided into three sections showing 1/3 fractions.

If we split a circle into three equal parts instead, we get Figure 3. Each colored sector is one-third of the full circle, so the fraction is 1/3 (a common fraction). Thus, adding them up gets us 1/3 + 1/3 + 1/3 = 3/3 = 1, which is the full circle. 

Further Classification: Proper and Improper Fractions

A common fraction is further classified as a proper fraction if the numerator is smaller than the denominator and improper otherwise. For example, 2/10 and 19/77 are common, proper fractions. On the other hand, 13/8 and 89/29 are common and improper fractions. Fractions with decimal values like 3.75/2, 5/2.5, and 1.2/9.3 are not common fractions. 

However, even though there are no decimals in a common fraction, its result can still be a decimal number. If the common fraction is improper and the numerator is additionally a multiple of the denominator, the result is an integer. If either of those is not the case, we get a decimal number instead.

There are several methods and shortcuts to evaluate common fractions, but the most straightforward – though slightly longer approach – is to use long division (see examples). As with all fraction types, you can simplify a common one – 2/10 is the same as 1/5!

Common Fractions in Real Life

It is easy to make sense of common fractions because they represent the division of whole things – we use them everywhere in real-life situations!

For example, suppose you have a pack of 10 whole biscuits and want to share it equally with your best friend from class. The fraction for this scenario is 10/2, which is a common, improper fraction. Because 10 is a multiple of 2, the result is an integer. It evaluates to 5, which means you and your friend get five biscuits each!

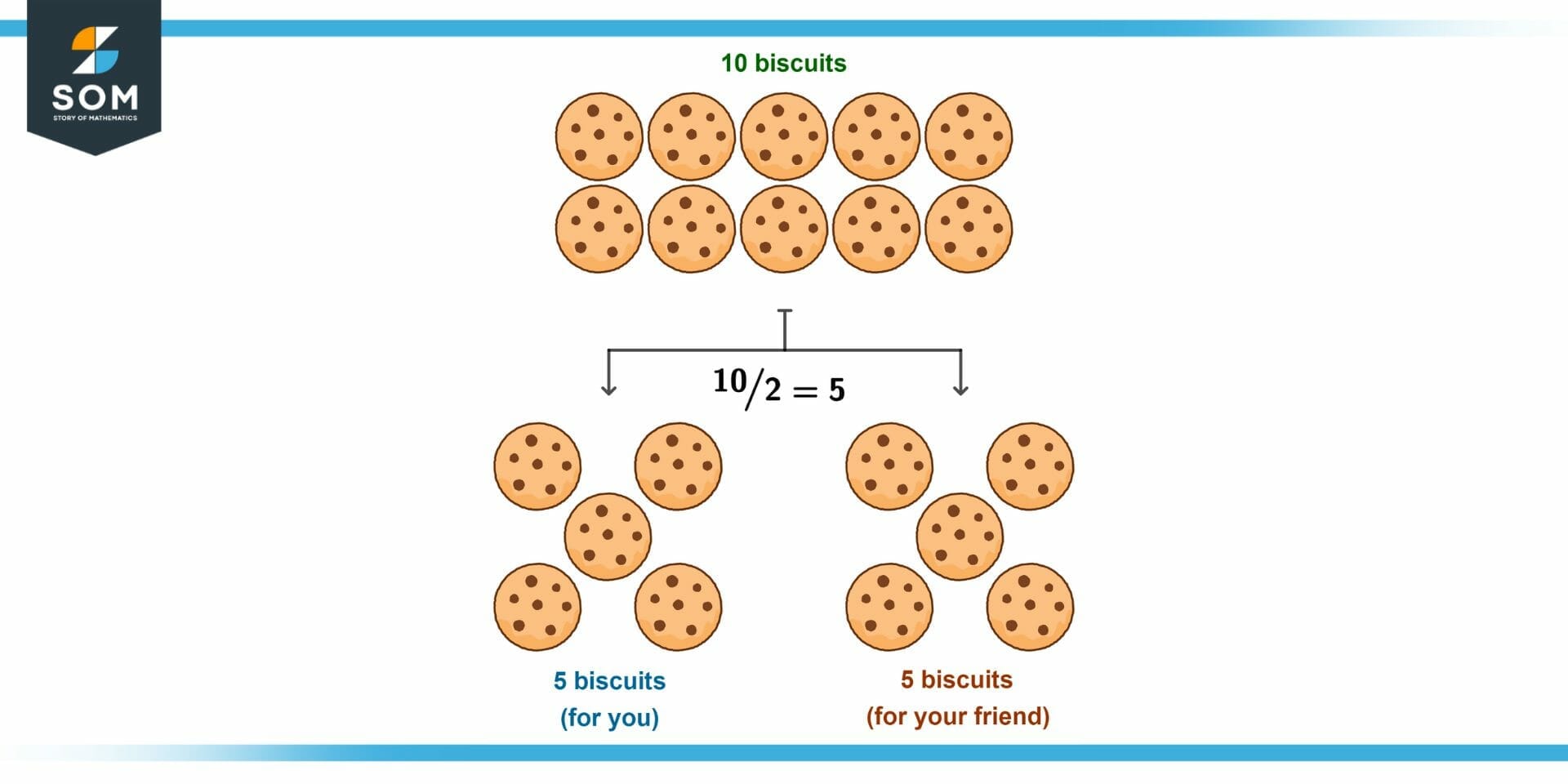
Figure 4 – Dividing biscuits among friends is an example of a common fraction at work!

However, what if one of the biscuits broke? You can still represent this as a fraction (e.g., 9.5 biscuits if half of a biscuit broke off), but this is a decimal fraction, not a common one.

Now suppose that you only had one biscuit. Then, the fraction would have been 1/2 (common and proper). Thus, you and your friend both get half a biscuit. If you wanted to share it with two friends, the fraction would be 1/3, and everybody would get one-third of the biscuit, and so on.

Sometimes, the result of a common fraction does not make much sense. For example, if you had to seat 20 people in a bus with only 18 seats, the fraction implies that there should be 20/18 = 10/9 = 1.11 (one person and roughly one-eleventh of another) people per seat. 

Since one-eleventh of a person cannot be on a seat, this is not directly helpful. Still, it tells us that two people must share the seats with the others. On the contrary, if we only had ten seats, the fraction becomes 20/10 = 2. That is, everyone has to share the seats.

Thus, when you are dividing a whole number of things into a whole number of groups, the fraction directly representing this would be a common fraction.

Solving Fractions – An Example

What is the result of the common fraction 25/100? If possible, simplify before using long division. Using the result of 25/100, what would be the result of 50/100?

Solution

Dividing the numerator and denominator by 25 simplifies the fraction to 1/4 (since 25/25 = 1 and 100/25 = 4). Thus, 25/100 = 1/4, meaning one-fourth of 100 is 25. Since this is a proper fraction, the result will be a decimal and smaller than 1. 

Now let us solve 1/4 using the long division method. The numerator 1 is the dividend, and the denominator 4 is the divisor. The result of the division is the quotient.

To divide, we need the dividend to be greater than the divisor. Since this is not the case (1 < 4), we multiply 1 x 10 = 10, which is now greater than 4. 

To indicate this first multiplication by 10, we add a decimal point “.” to the quotient.

Now, we divide the new dividend 10 by 4:

10 $\boldsymbol\div$ 4 $\boldsymbol\approx$ 2

Where 2 is the first decimal digit of our quotient such that:

4 x 2 = 8

That gets us the remainder 10 – 8 = 2. Now, we must divide the remainder by 4. Since 2 < 4, we multiply it by 10 to get 2 x 10 = 20. We now divide 20 by 4:

20 $\boldsymbol\div$ 4 = 5

Where 5 is the second decimal digit of our quotient:

4 x 5 = 20

That gets us a zero remainder since 20 – 20 = 0. Thus, our result (the quotient) is 0.25 = .25, a terminating, non-recurring decimal number. 

Since 50/100 is twice that of 25/100, the result of 50/100 is twice that of 25/100. Thus:

50/100 = 2 x 25/100 = 2 x 0.25 = 0.5

All mathematical drawings and images were created with GeoGebra.

Common Factor Definition < Glossary Index > Common Multiple Definition