Common Multiple|Definition & Meaning

Several numbers share the same multiples. The term “common multiple” refers to them. For instance, take 2 and 4. We want to compute the common multiple of these two numbers. For that purpose, we will first make a list of 2 multiples, and secondly, we will make a list of 3 multiples. The common multiple will be the number that will occur in both lists or, in other words, is common in both lists. 

Multiples of 2 can be written as 2, 4, 6, 8, 10, 12, and continued. We can write 4’s multiples as 4, 8, 12, 16, 20, 24, 28, and so on. On figuring out the common values between the two lists, we got 4 and 8, and 12, so these three numbers are common multiples of 2 as well as 4.

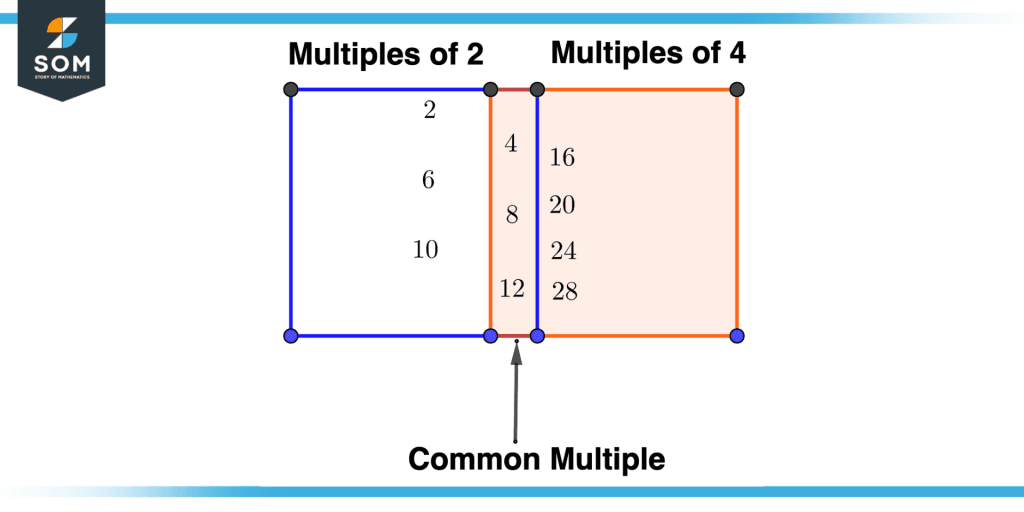
Figure 1 – Explanation of Common Multiple

Properties of Common Multiple

1. There is an unlimited (infinite) common multiple of any two numbers.
2. The common multiple of two numbers is divisible by both numbers.
3. In mathematics, a number’s common multiple is greater or equal to its number.
4. A common multiple of two numbers will be the product of those two numbers with some other number.

Proof of Property 1

There is an unlimited (infinite) common multiple of any two numbers.

Consider two numbers, 2 and 4. The multiple of both numbers will be infinite as we know that we get the multiples of a number by multiplying it with a range of numbers starting from 1 to infinity. Therefore, we will get an infinite list of multiples same goes for the second number, so we have a list of multiples of two numbers that are infinite, so the common multiple (a common number in two lists) will also be infinite. This is shown by an illustration. 

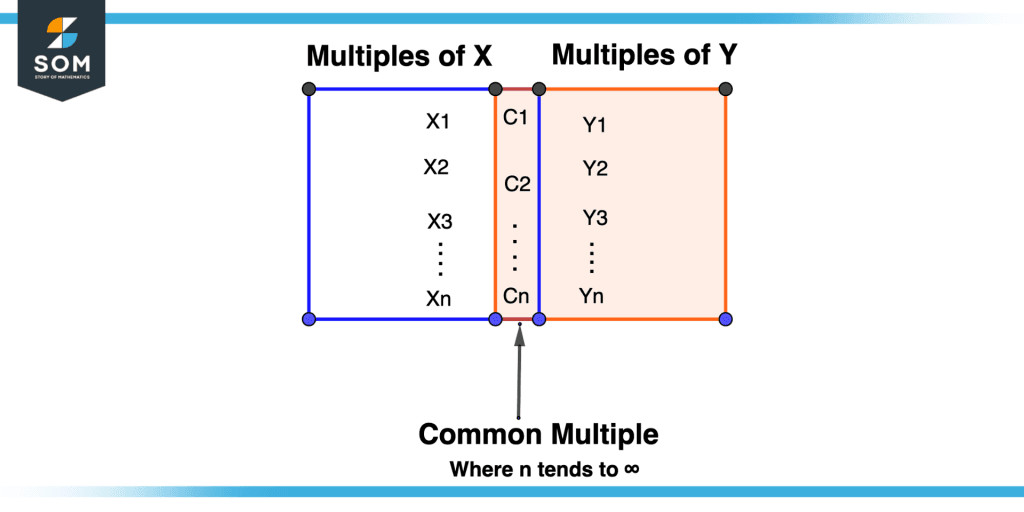
Figure 2 – Proof of Property One

Proof of Property 2

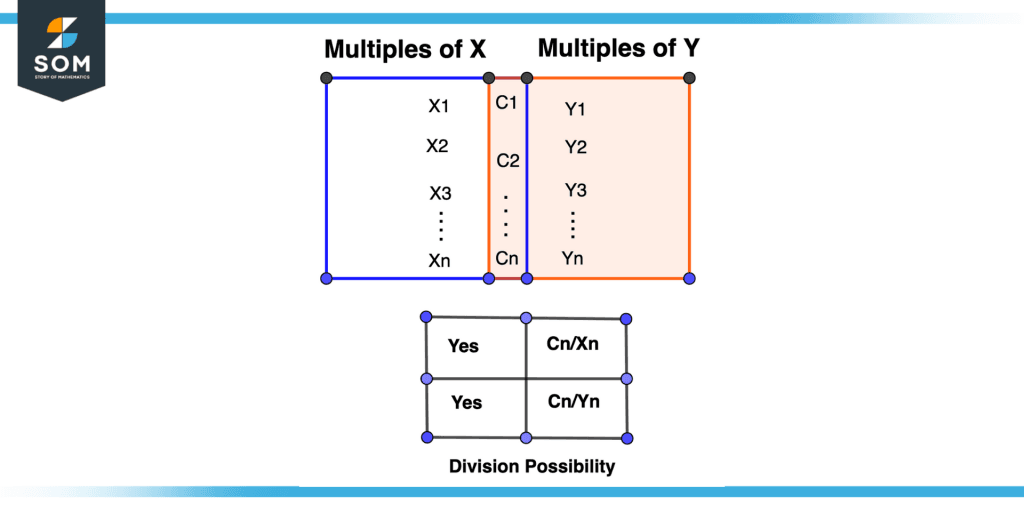
Figure 3 – Proof of Property Two

The common multiple of two numbers is divisible by both numbers.

Consider two numbers, 2 and 4. The finite common multiple lists of two numbers are shown. We can see 4, 8, and 12 are the common multiple of 2 and 4 so if we divide them by 2 and 4 they are easily divisible as shown. We can see that the common multiple 4 of number 2 and number 4 is divisible by both numbers.

Proof of Property 3

In mathematics, a number’s common multiple is greater or equal to its number.

Consider two numbers 2 and 4. We can see from the list of their common multiple that every common multiple is either greater or equal to the number.4, 8, and 12 are greater than 2 and 8, 12 is greater than 4 and 4 is equal to 4. None of the common multiples is less than the number itself.

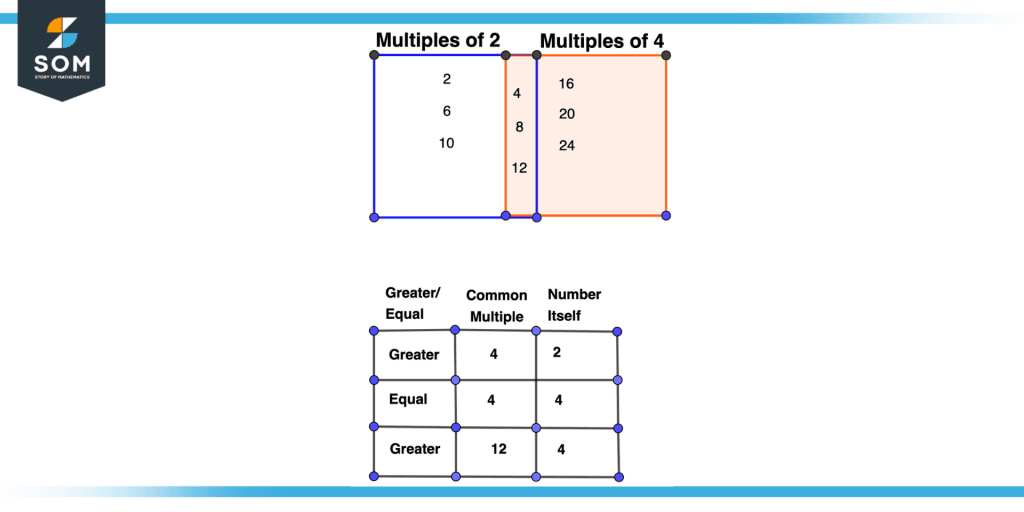
Figure 4 – Proof of Property Three

Proof of Property 4

A common multiple of two numbers will be the product of those two numbers with some other number.

Consider two numbers 2 and 4. We know that 4, 8, and 12 are the common multiple of both numbers so generally, they are the product of the number of which they are common multiple ( 4 and 2) with some whole number. We can clearly say that the common multiple 4 of number 2 and number 4 is equal to the number itself multiplied by another whole number.

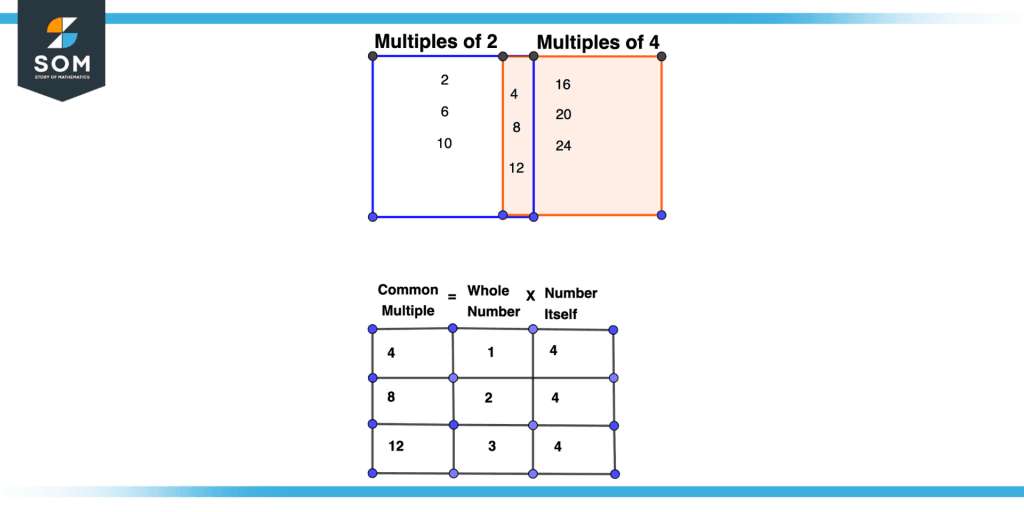
Figure 5 – Proof of Property Four

Steps to Compute Common Multiple of Two Numbers

Step 1: Given 2 numbers, x and y, make the list of multiple of both numbers like this.

List1: Multiples of First Number (X)

List2: Multiples of Second Number (Y)

Step 2: Highlight those multiples that are common in both list

List1: a, b, c, d, e, f (Multiples of X)

List2: h, i, j, k, d, c   (Multiples of Y)

Step 3: Make a new list containing the common numbers in both lists.

Common Multiple of X and Y= c, d

Least Common Multiple

LCM is the least common multiple of the two numbers, given two numbers x and y, and their multiples as List 1 and List 2, LCM would be the smallest common number between List 1 and List 2. If you have more than one number, you can also calculate it. To find the LCM, there are various methods available.

For the fast computation of LCM of two numbers, one approach is to factorize each number and then, by multiplying their highest powers, find the product of the prime factors they have in common. The general process is detailed below:

Step 1: Given two numbers, x and y, make a list of multiple numbers like this.

List 1: Multiples of First Number (X)

List 2: Multiples of Second Number (Y)

Step 2: Highlight those multiples that are common in both lists.

List 1: a, b, c, d, e, f (Multiples of X)

List 2: h, i, b, k, d, l   (Multiples of Y)

Step 3: Make a new list containing the common numbers in both lists

Common Multiple of X and Y= b, d

Step 4: Out of the list of common multiples, the smallest number in that list will be the LCM.

Properties of Least Common Multiple

• When two or more prime numbers are multiplied together, the LCM is the product of those numbers.
• Considering two or more numbers, Least common multiple will always be greater than or equal to each number individually.

Solved Problems on Finding the LCM

Example 1

Find 4 Common Multiples of three numbers 2, 4, and 8.

Solution

Step 1: Given three numbers 2, 4, and 8.

List 1: 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32

List 2: 4,8,12,16,20,24,28,32,26,34

List 3: 8,16,24,32,40,48,56,64,72,80

Step 2: Highlight those multiples that are common in both list

List 1: 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32

List 2: 4,8,12,16,20,24,28,32,26,34

List 3: 8,16,24,32,40,48,56,64,72,80

Step 3: Make a new list containing the common numbers in both lists

Common Multiple of 2,4 and 8= 8,16,24,32

Example 2

Find the Least Common Multiple of the two numbers 3 and 6.

Solution

Step 1: Given two numbers 3 and 6:

List 1: 3,6,9,12,15,18,21,24,27,30

List 2: 6,12,18,24,30,36,42,48,54,69

Step 2: Highlight those multiples that are common in both list

List 1: 3,6,9,12,15,18,21,24,27,30 

List 2: 6,12,18,24,30,36,42,48,54,60

Step 3: Make a new list containing the common numbers in both lists.

Common Multiple of 3 and 6= 6,12,18,24,30

Step 4: The smallest number from the common multiple lists is 6, which is the LCM of 3 and 6.

All images/mathematical drawings were created with GeoGebra.

Common Fraction Definition < Glossary Index > Common Ratio Definition