Common Ratio|Definition & Meaning

There are three types of fundamental sequences in mathematics called arithmetic, geometric and harmonic sequences. The geometric sequences are multiplicative sequences.

Such types of sequences have the property that each of the terms is a scalar multiple of the previous term. This scalar multiple is called the common ratio. 

A geometric sequence can be completely defined by any of the elements and the common ratio. Theoretically, the whole sequence is reconstructed using these two numerical values only.

Mathematical Form of the Common Ratio

Let us say that we have a sequence of numbers as shown below:

{ 1, 3, 9, 27, …… }

The following figure displays this sequence:

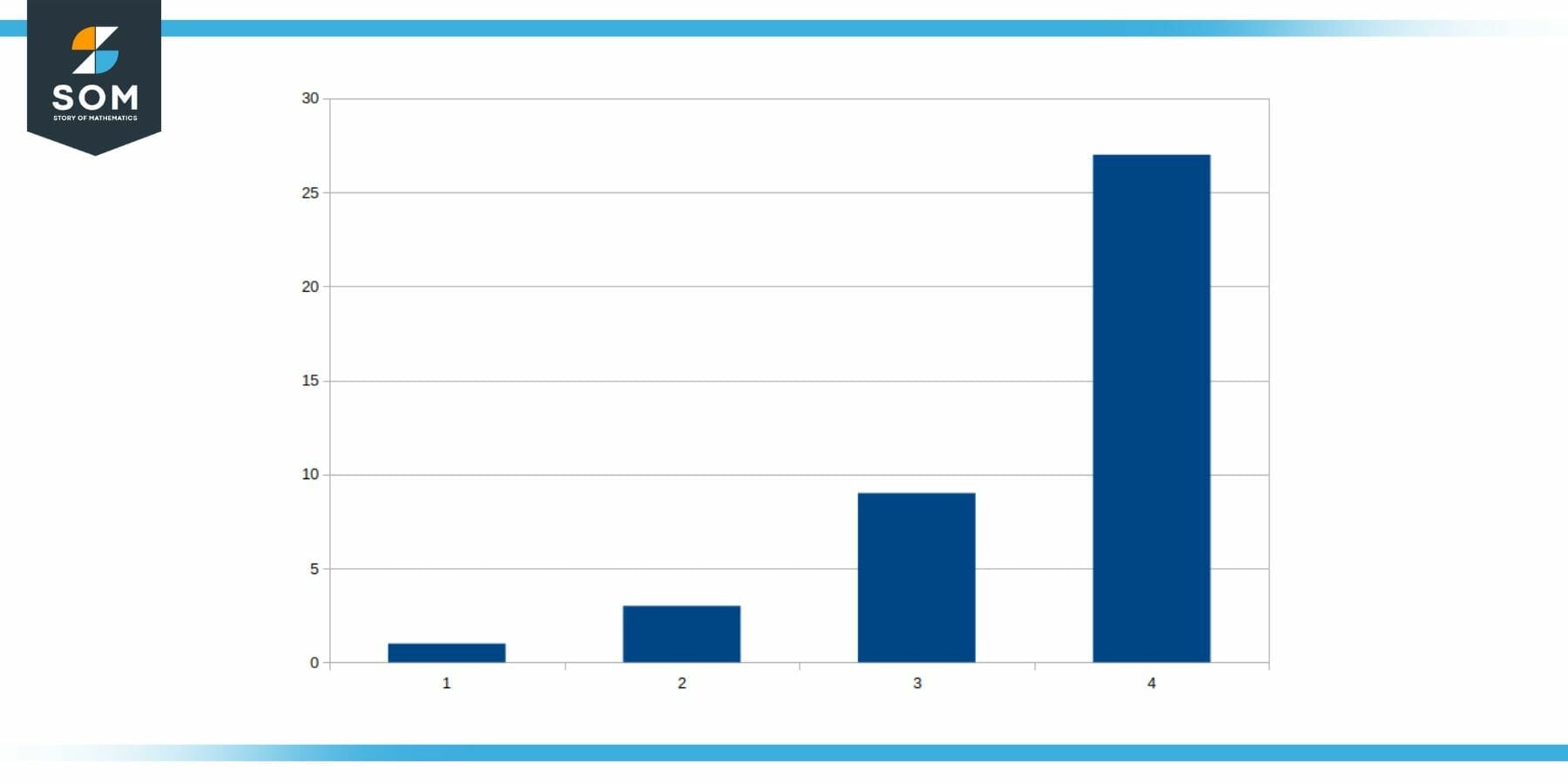
Figure 1: Common Ratio in Geometric Sequences

Let us calculate the ratio of the 2nd and 1st elements:

\[ \dfrac{\text{2nd element}}{\text{1st element}} \ = \ \dfrac{ 3 }{ 1 } \ = \ 3 \]

Now let us calculate the ratio of the 3rd and 2nd elements:

\[ \dfrac{\text{3rd element}}{\text{2nd element}} \ = \ \dfrac{ 9 }{ 3 } \ = \ 3 \]

You may notice that the ratio of the 2nd and 1st elements is equal to the ratio of the 3rd and 2nd elements. We can see that the ratio of each consecutive pair of elements in the above sequence equals 3. Since the ratio is constant, we can say that the given sequence is a geometric sequence, and the ratio that stays constant is called its common ratio.

The above sequence can be completely described by the 1st element (1) and the common ratio (3). Given these two values, we can construct the sequence as follows:

{ 1, 1(3), 1(3)(3), 1(3)(3)(3), 1(3)(3)(3)(3), ……. }

It can be reduced to:

\[ \{ \ 1(3)^0, \ 1(3)^1, \ 1(3)^2, \ 1(3)^3, \ 1(3)^4, \ ……. \ \} \]

Which is equal to the original sequence.

The above version of the given sequence leads to the general form of a geometric sequence which is given below:

\[ a_n \ = \ a_1 \ r^{ n – 1 } \]

Here, $ a_n $ is the $ n^{th} $ element, $ a_1 $ is the $ 1^{st} $ element and $ r $ is the common ratio. Using this formula, we can write the expression for the $ (n-1)^{th} $ element:

\[ a_{ n – 1 } \ = \ a_1 \ r^{ n – 2 } \]

Dividing above two equations, we can derive the expression for the common ratio:

\[ \dfrac{ a_n }{ a_{ n – 1 } } \ = \  \dfrac{ a_1 \ r^{ n – 1 } }{ a_1 \ r^{ n – 2 } } \]

\[ \dfrac{ a_n }{ a_{ n – 1 } } \ = \  r^{ n – 1 – ( n – 2 ) } \]

\[ \dfrac{ a_n }{ a_{ n – 1 } } \ = \  r \]

Rearranging:

\[ r \ = \  \dfrac{ a_n }{ a_{ n – 1 } } \]

Explanation of Common Ratio Using Examples

Spreading of a Virus

The spreading of a virus or a bacterial infection in a population is an example of geometric progression. Whenever a virus outbreak occurs in a population, the scientists define the R value of the virus. This R value tells us how many other people can get infected from a single person. This R value is nothing but the common ratio.

Consider the case of coronavirus pandemic. The R value or the common ratio of this virus is around 2.5. This means that if one of the persons gets infected, it will spread it to 2.5 others. We can construct a geometric sequence using 1 as the first number and the value 2.5 as common ratio:

{ 1, 2.5, 6.25, 15.63, 39.06, …… }

The following figure shows a chart of this progression.

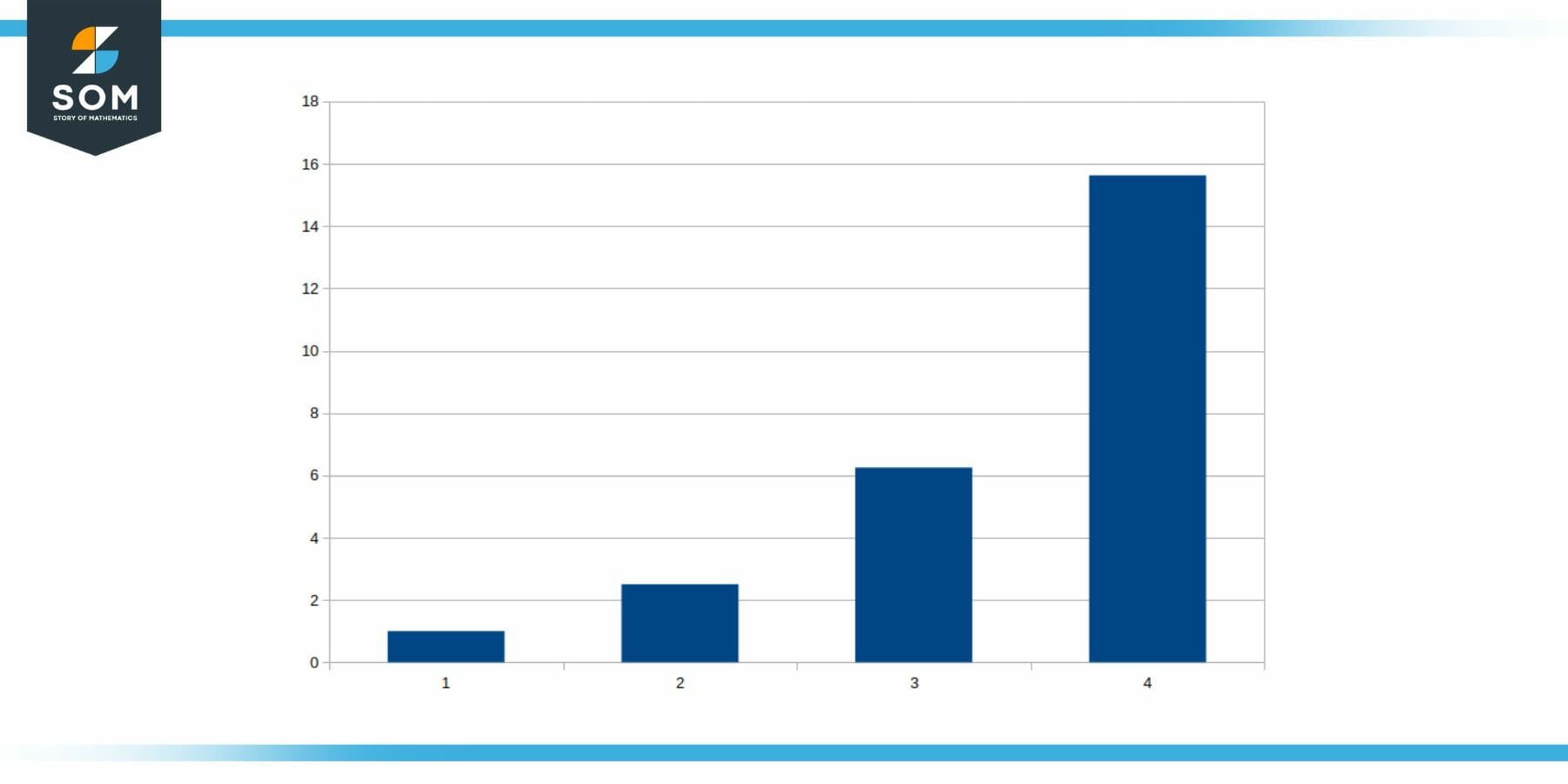
Figure 2: Common Ratio in Spreading of Coronavirus Outbreak

Nuclear Chain Reaction

Another very interesting example can be the nuclear fission chain reaction used in the nuclear power plants. Whenever an atom splits, its called nuclear fission. Each fission event is caused by the collision of a high speed neutron. The fission reaction may release two new high speed neutrons that further collide with the other nuclei and create a chain reaction. This process can also be modeled using the geometric progression and common ratio.

Lets say that their is only one high speed neutron at the start $ a_1 \ = \ 1 $ and each fission reaction releases two neutrons $ r \ = \ 2 $. We can construct the sequence of no. of fission reactions as follows:

{ 1, 2, 4, 8, 16, …… }

This process can be shown in the form of a graph as follows:

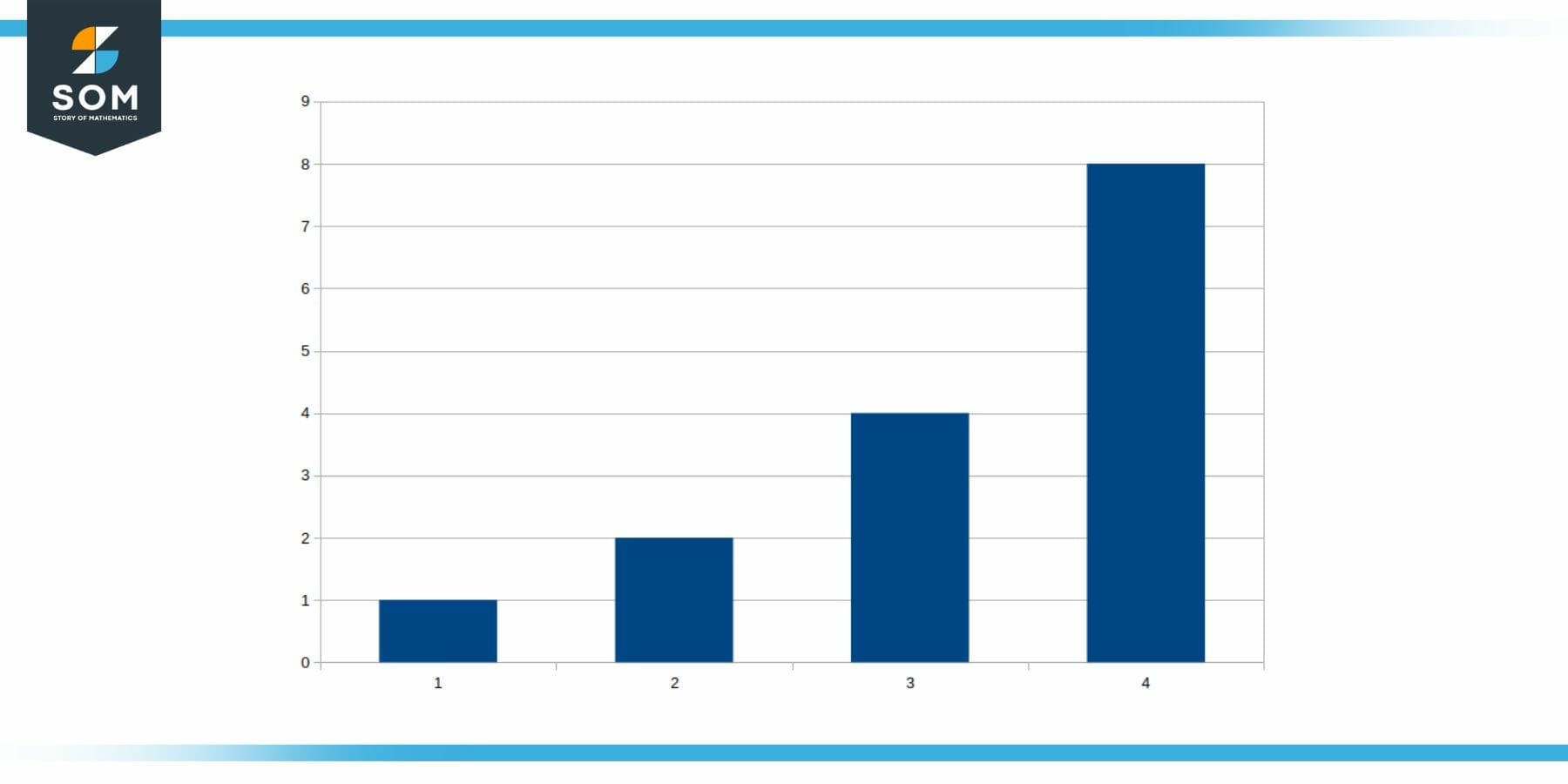
Figure 3: Common Ratio in Nuclear Chain Reaction

Use of Logarithmic Scales in Common Ratio

The geometric progressions are exponential, hence its very useful to use logarithmic scales for their graphs. Consider the following figure where the spreading of coronavirus is plotted over long term.

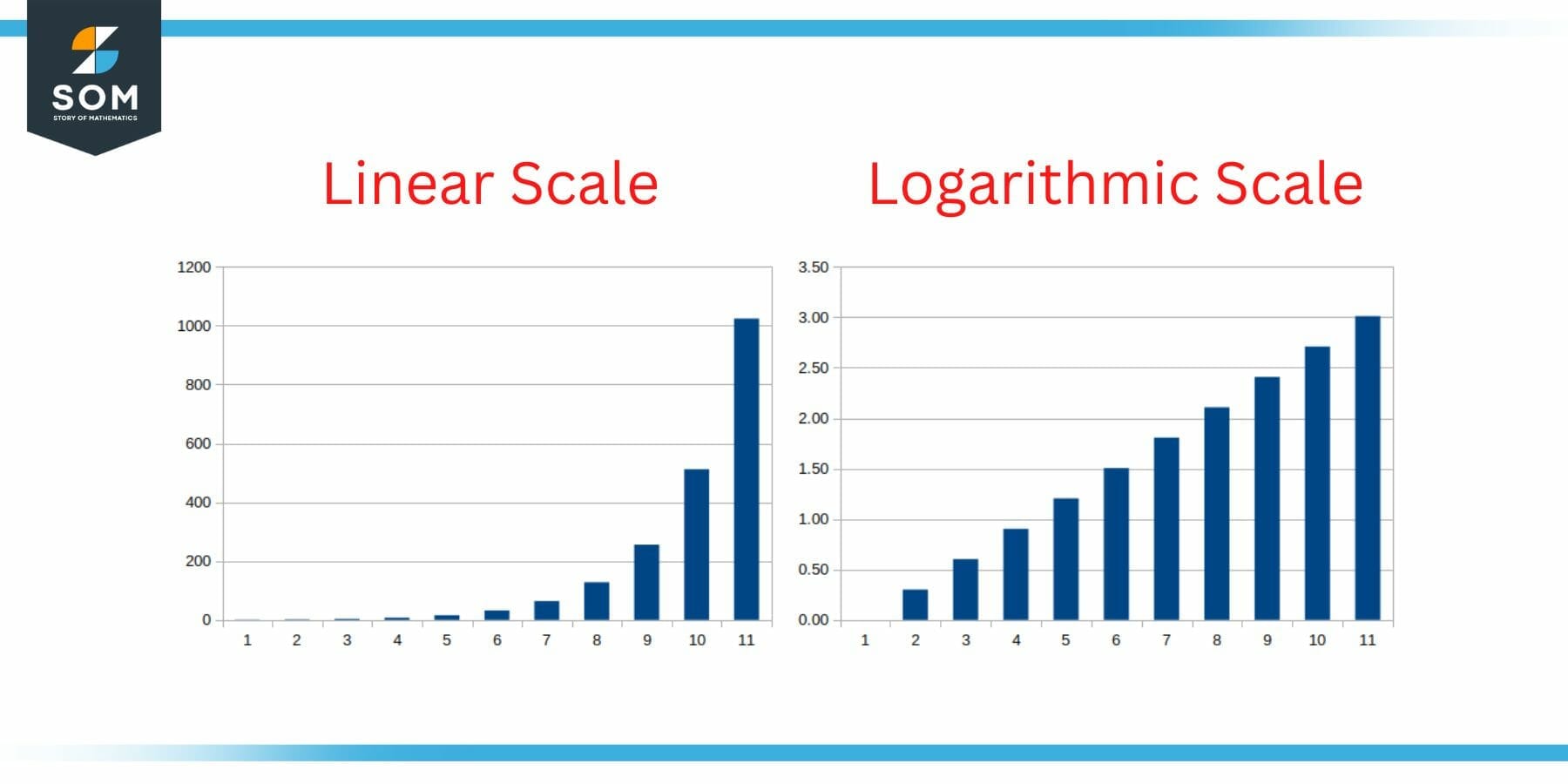
Figure 4: Logarithmic Scale for Common Ratio and Geometric Sequences

It can be clearly seen that the logarithmic scale is more readable over long-term data. Logarithms are often used in the calculation of common ratios for numerical problems of complex nature.

A Numerical Example of Common Ratio

Part (a): The 3rd and 4th elements of a geometric progression are 2.25 and 3.375 respectively. Find the common ratio.

Part (b): The 5th element of a geometric progression is 625 and its common ratio is 5, then calculate the value of first element.

Part (a) Solution

Given that:

\[ { a_{ n – 1 } } \ = \ 2.25 \]

\[ { a_n } \ = \ 3.375 \]

Using the formula:

\[ r \ = \ \dfrac{ a_n }{ a_{ n – 1 } } \]

r = 3.375 / 2.25

r = 1.5

Which is the value of common ratio.

Part (b) Solution

Given that:

r = 5

n = 5

\[ a_n \ = \ 625 \]

Using the formula:

\[ a_n \ = \ a_1 \ r^{ n – 1 } \]

\[ 625 \ = \ a_1 \ ( 5 )^{ 5 – 1 } \]

\[ 625 \ = \ a_1 \ ( 5 )^{ 4 } \]

\[ 625 \ = \ a_1 \ (125) \]

Rearranging the above expression,

\[ a_1 \ = \ \dfrac{ 625 }{ 125 } \]

\[ a_1 \ = \ 1 \]

Which is the first value of the sequence.

All figures and graphs have been constructed using GeoGebra.

Common Multiple Definition < Glossary Index > Compass Drawing Definition