JUMP TO TOPIC
Compass (Drawing)|Definition & Meaning
Definition
A compass is a drawing instrument used in geometry to draw circles, and arcs and measure distances.
Design of Compass
Compasses typically have two legs that connect at a joint and are constructed of metal. The circle’s or arc’s size can be adjusted by moving legs apart depending upon the measurements. The ends of one component are sharp, pointed spikes, and the other is a pencil. Design of a compass is illustrated in figure 1
Figure 1- Compass
Compasses come in two varieties that are mechanical and conventional. A mechanical compass has a mechanical pencil and a conventional or normal compass has a normal pencil.It is simple to locate the compass that is most suited for the circle you wish to create because there are many different compasses, both large and little, accessible for selection.
When drawing a stroke, align the legs perpendicular to the paper if one or both of them have joints. Make a full stroke with the compass in a single motion without pausing or going backward to optimize stroke quality. The compass may be used with an extension bar to draw circles with up to a 25 cm diameter.
When using the compass needle to draw many circles with the same center, it’s possible to make a sizable hole in the paper. A center disc can be quite helpful in these circumstances. A center disc keeps your circles’ centers true and shields the paper from tearing. A circle template is an additional tool for drawing circles.
The user turns the compass to create circles and arcs by using the leg with the needle as an axis. Compass writing implements include mechanical pencils, pencil lead, and sketching pens. Certain compasses are made to let the user switch between writing tools.
Uses of Compass
A compass is used for drawing circles, arcs and measuring distances on maps. You may draw circles by placing the pencil on the paper, pushing the pencil’s spiked leg into the paper, and then tracing a circle with the pencil. To achieve this, you must avoid moving the legs in any direction while you are drawing the circle.
By adjusting the distance between the legs, a circle may be made larger or smaller. Distance between the legs depends upon the radius of a circle.
Dividers and compasses with two spikes can be used to measure distances on a map. The distance between the spikes on the map represents a real-world distance. The distance between two points on a map may be determined by counting how many times the compasses fit between them.
Drawings with a compass and straightedge are used to illustrate concepts in planar geometry. On paper, actual compasses are utilized, but the ideal compass employed in proofs is a fictitious, ideal device that creates ideal circles.
The “collapsing compass” is the most exact characterization of this perfect explanation instrument. It can only be used once and creates a circle with the provided radius from the supplied location. That is to say, it cannot simply be transferred to another location and utilized to create another identical circle like a real pair of compasses.
Angles can also be constructed using compasses and rulers. After drawing a line segment AB takes O as a center point to draw and an arc then using the end of the arc as a center point we make the first cut on the arc which represents the 60-degree angle.
Then using 60-degree angle as the center make another cut on the arc which shows the 45-degree angle the using both the cut of 60 and 45 we make two cuts which show the angle of 90 degrees. We can also plot the angle of 135 by taking 45 degrees and the other end of the arc as the center as shown in figure 1.
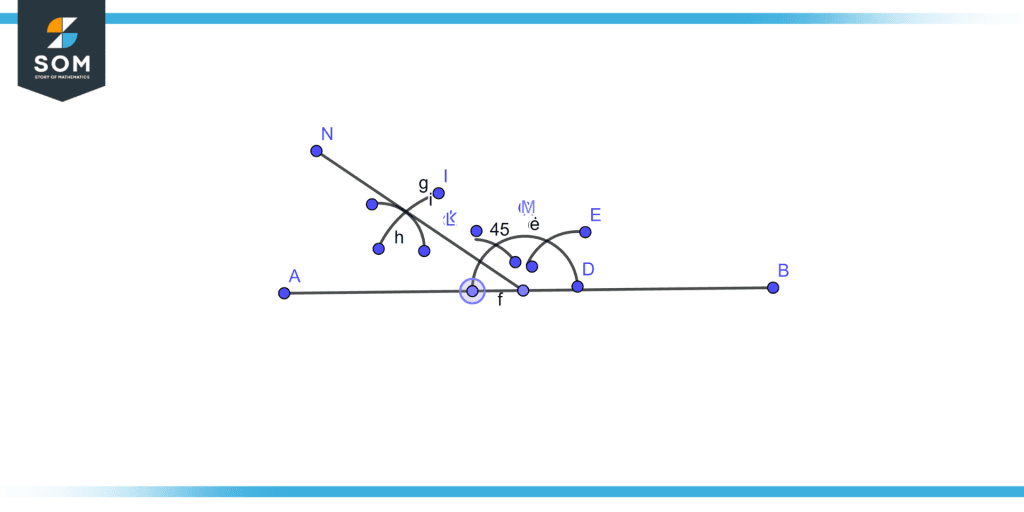
Figure 2 – Angle using compass
Different Variants of Compasses
A beam compass is a tool used for drawing and dividing circles that are bigger than those produced by a typical pair of compasses. Scribe compasses are the simplest form of the compass. The metal branches on both are crimped. While one branch has a pencil sleeve, the other is crimped and has a point sticking out at the end.
Loose-leg wing dividers are used to step off repeating measurements and draw circles with some precision. The brass pivot, thumb screws, pencil holder, and branches are all well-constructed.
A proportionate compass also referred to as a military compass or sector—was a tool used for calculating. It is made up of two equal-length rulers connected by a hinge. On the rulers are many scales that can be used for mathematical calculations. To decrease or increase patterns while maintaining angles, a reduction compass is utilized.
Drawing Different Geometries With a Compass
Example 1
Draw a circle having a radius of 2 cm with a compass.
Solution
Open the legs of the compass of 2 cm and put the pointed spike at a point i.e. A and then draw the circle as illustrated in figure 2.
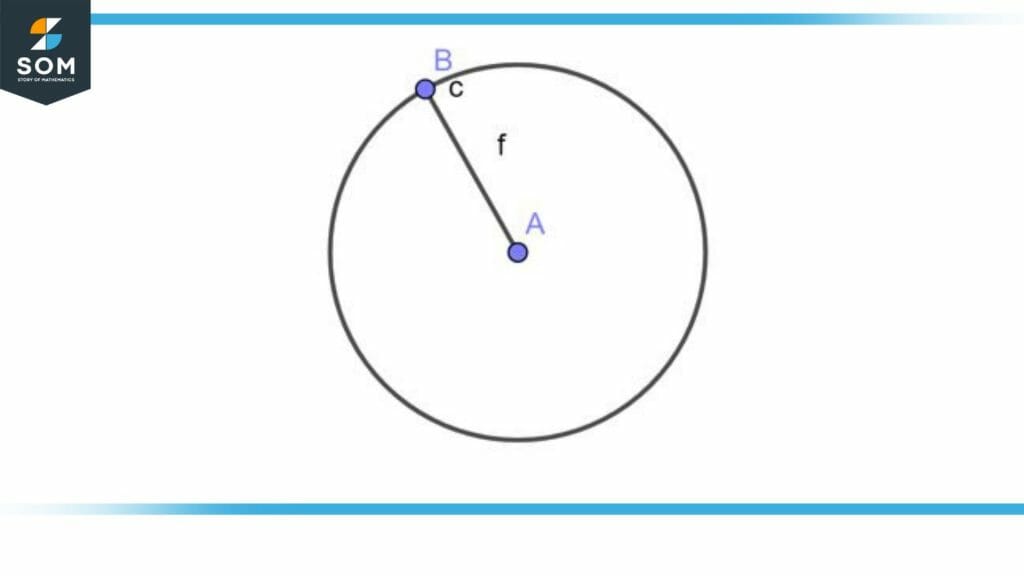
Figure 3 – Circle by compass
Example 2
Draw an arc of radius 2 cm with a compass.
Solution
Open the legs of the compass of 2cm and put the pointed spike at a point i.e. A and then draw an arc between B and C as illustrated in figure 3.
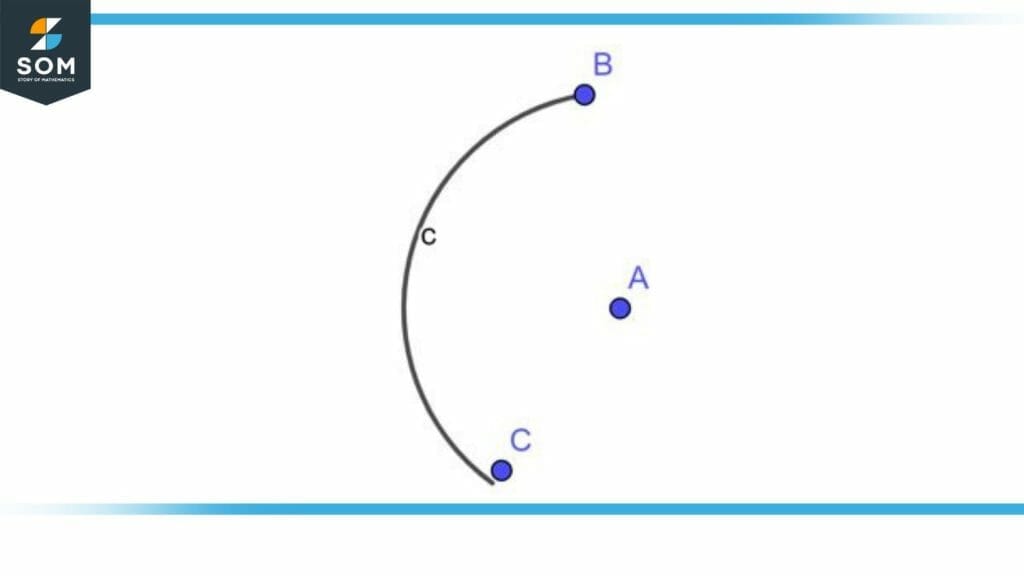
Figure 4 – Arc by compass
Example 3
Draw an angle of 90 degrees with a compass.
Solution
Draw a line segment OA. Draw an arc cutting the line segment OA at point B with a small radius. Using the same radius, fix the compass at B and arc cutting the first arc at C. Again, keeping the same radius, fix the compass at C and draw an another arc cutting the first arc at D. Draw two arcs using C and D to join at E. Then pass a line segment through O and point E as illustrated in figure 4.
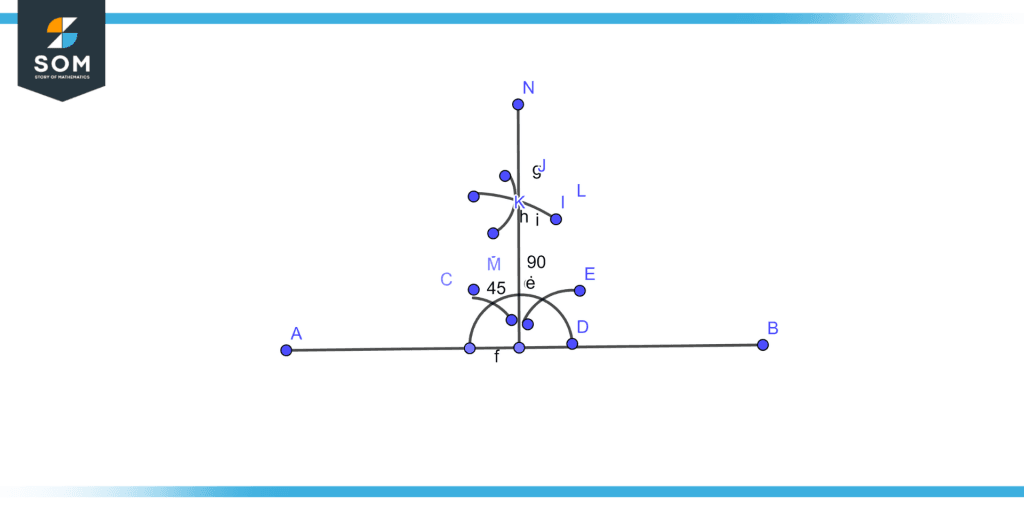
Figure 5 – Ninety degrees angle using compass
All images/mathematical drawings were created with GeoGebra.
