Complement Probability|Definition & Meaning

What Are Complementary Events? 

Two events are complementary if and only if their occurrence is dependent on the absence of the other. When two occurrences are mutually exclusive and exhaustive, we say they are complementary.

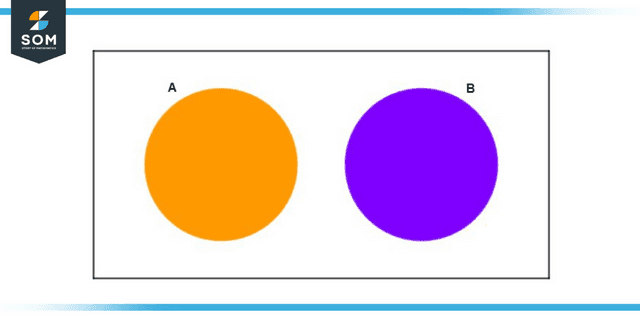
Figure 1: Mutually Exclusive Events

In the diagram above, the event A and the event B are mutually exclusive, meaning that their elements do not match. There is no intersection between both events.

Probabilities of mutually exclusive occurrences must add up to 1. Events can only occur in a complementary manner if there are precisely two possible outcomes. This article will provide some background information about complimentary occurrences and some illustrations.

In the Probability field, there are two probable outcomes for an event to be complementary. Take, for instance, the difference between passing and failing a test. One way to think of an event is the collection of results that an experiment produces. As a result, occurrences will consistently constitute a portion of the sample space.

Properties of Complementary Events

For two occurrences to be considered complimentary to one another, they need to exhibit specific characteristics. These are presented in the following order:

Complementary events are exhaustive and mutually exclusive, which implies events that are complementary to one another cannot coincide. This indicates that two occurrences that are complementary cannot occur at the exact moment. In other words, complementary events do not co-occur.

Events that complement one another are thorough. This suggests that an event and its complement must fill up the sample area for it to be considered valid. Thus, S = A ∪ A’

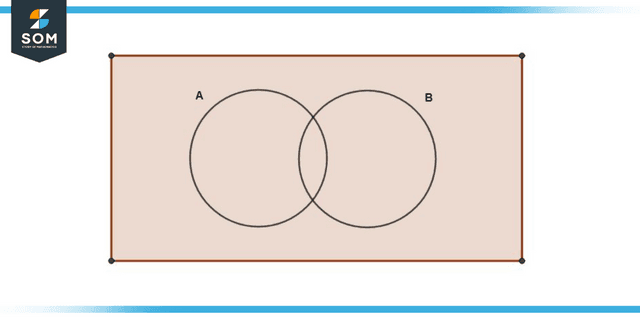
Figure 2: Representation of S = A ∪ A’

The diagram shown above shows two sets of probability that represents the complement probability concept. The shaded area shows the entire sample space.

Rules of Complementary Events

According to the concept of complementary events, the total of the probabilities that an event will occur and the probabilities that the event’s complement will also occur will always equal 1. Let’s say there’s an event denoted by the letter A, and let’s call the likelihood of its happening P(A). Therefore, the chance that A will not occur is denoted by the P(A) symbol. Following is a mathematical expression that can be used to describe this rule.

1. P (A) + P (A’) = 1
2. P (A) = 1 – P (A’)
3. P (A’) = 1 – P (A) (A)

These three mathematical assertions are all identical to one another.

Examples of Complementary Events

Let us consider that we roll two dice. Let’s call this occurrence B when you obtain two different digits. Find P (B).

Because it is a more straightforward method, we will apply the rule of complimentary events to solve this example.

Let us call the occurrence described by B’ the one in which the digits on both dice are the same or do not differ. The formula for determining the sample space for B’ is as follows: S’ = [(1, 1), [(2, 2), [(3, 3), [(4, 4), [(5, 5), and [6, 6]].

When two dice are rolled, there are a total of 36 possible results. The number of positive outcomes equals six.

P(B’) = 6 / 36 = 1 / 6

According to the rule of events that occur in complementary ways,

P(A) = 1 – P(A’).

P(B) = 1 – (1 / 6) = 5 / 6

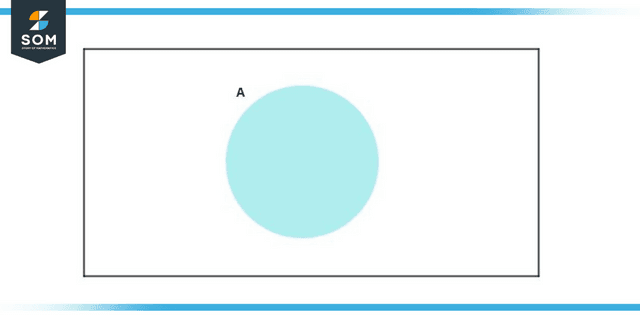
Figure 3: Representation of P(A) = 1 – P(A’)

Therefore, rolling two dice results in a five out of six Probability of getting two different numbers.

Odds in a Complementary Event

The odds don’t need to be even. The sum of the two probabilities, namely the probability that an event occurs plus the probability that it does not, must equal 1. This is the most crucial thing to keep in mind. The complementary activity of rolling a die to check if you receive six results in only two possible outcomes: either receiving a six (with a chance of one in six) or not getting a six (with a chance of five in six). If there is a one-in-a-million chance of you winning the lottery, then there is a 999,999 to one chance that you will not win. The two Probability are equivalent to one another:

Things To Remember

1. Complementary occurrences are those in which the occurrence of one event is contingent upon and is only possible in the absence of another event.
2. Events that are complementary to one another cannot co-occur and exhaust one another.
3. The sample space comprises an event and its associated complement when taken together.
4. The rule that governs complementary events states that P(A) + P(A’) = 1.

Some Examples of Complement Probability Problems

Example 1

A jar contains red balls and blue balls. If the probability of picking a red ball is 2/5, find the probability of blue ball being picked up?

Solution

P (B) = P (not picking a red ball)

= 1 – P (R)

= 1 – (2/5)

= 3/5

The probability of picking a red or blue ball is a complementary event. It is defined as below:

P (B) = P (R’) The compliment of R’ is the set of R

P (R’) = P (B)

Thus, the following can be brought up:

P (A) + P (A’) = 1

Example 2

There are 8 flowers in a pot of which 2 are red, 3 are black, 1 is blue, 2 are purple, and 2 are pink. The primary color event selection of flowers is X. Find P (X’).

Solution

X = {2 red, 1 blue}

Total number of flowers: 8

The favorable outcomes are three.

P (X) = 3/10

The rule of complementary events says: P(A’) = 1 – P(A)

P(X’) = 1 – (3 / 10) = 7 / 10

All mathematical drawings and images were created with GeoGebra.

Compass Points Definition < Glossary Index > Complement Set Definition