Complement (Set)|Definition & Meaning

See the complement of a set Venn diagram below, which clearly illustrates the complement of set A, or A’, for a better understanding. In this case, neither set A nor A’ is a part of the other. A and A’ is a subset of U.

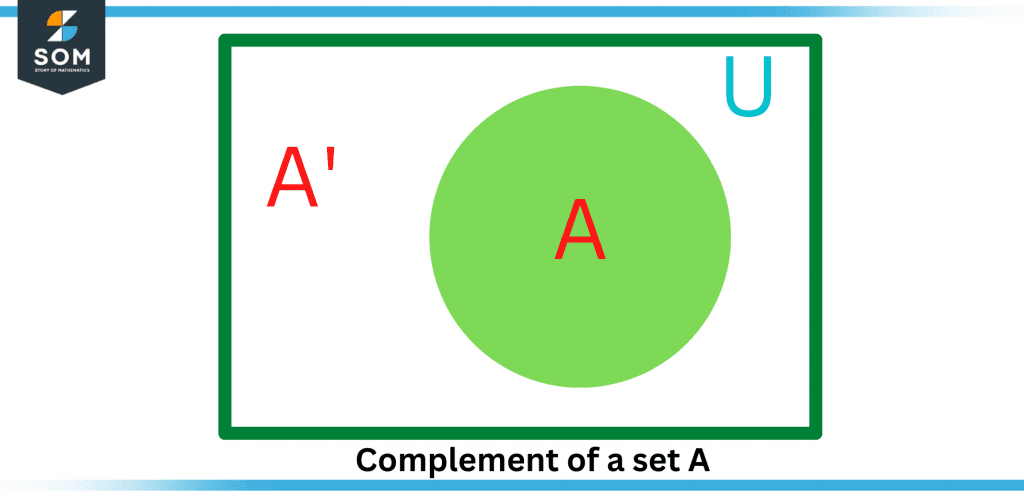
Figure 1 – Complement of set A

What Constitutes a Set’s Complement? 

If the universal set (U) contains the subset A, then the complement of set A, denoted as A’, is different from the elements of set A and contains both the universal set’s and set A’s components. In this case, A’ = {x ∈ U: x ∉ A}. In other terms, a set A’s complement is the difference between that set and the universal set.

Complement of Set Symbol

Any set’s complement is denoted by the letters A’, B’, C’, etc. To put it another way, if both the universal set (U) and a subset of it (A) are given, then the complement of the subset is given by A’ = U – A, which is the difference between the subset of the universal set (U) and the universal set (U).

If set A = 2, 3, and 5 and the universal set contains all prime numbers up to 25, then the complement of set A is something other than the elements of A.

Step 1: Look for the universal set and the set whose complement must be found. U = {23, 5, 3, 11, 13, 7, 19, 17, 2}, A = {5, 2, 3}.

Step 2: Subtract (U – A). In this case, U – A = A’ = {23, 5, 3, 11, 13, 7, 19, 17, 2} – {5, 2, 3}

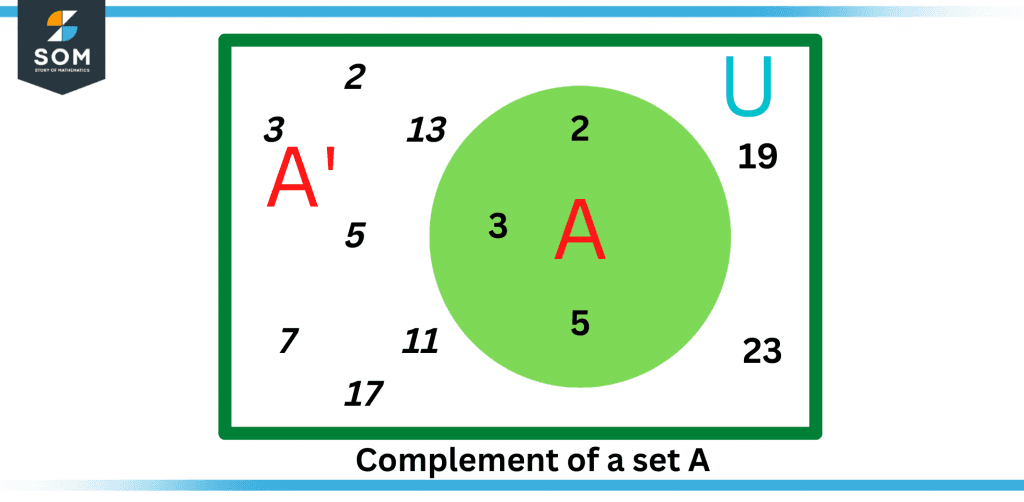
Figure 2 – Illustration of the complement of a set A with defined values.

Characteristics of a Set’s Complement

The complement of a set has the following properties, which include de Morgan’s law, complement laws, the laws of universal sets, empty sets, and double complementation.

Complement Laws

The universal set is denoted by the formula A ∪ A’ = U if A and A’ are both subsets of the universal set and A is one of them.

The empty set “,∅” indicated by  A ∩ A’ = ∅ is produced by the intersection of Set A and Set A’.

For example, If U = {9, 10, 11, 12, 13, 14, 15 } and A = { 9, 10} and B = {11, 12}

A’ = {11, 12, 13, 14, 15 } and B’ = {9, 10, 13, 14, 15}

A ∪ A’ = U = { 9, 10, 11, 12, 13, 14, 15}

and also, A intersection A’ = ∅

Double Complementation Rule

The original set, (A’)’ = A, is the complement of the complemented set according to this law.

The double complement of A is hence the complement of the set A′, where A′ is the complement of A itself.

In the previous example, if U =9, 10, 11, 12, 13, 14, and 15 and A = 9 and 10 then A’ = 11, 12, 13, 14 and 15.

Set A is equivalent to the complement of A’, which is (A’)’ = {9, 10}.

Universal Set and the Law of Empty Set

The complement of the universal set contains no elements since the universal set is exhaustive. This type of set is called an empty set, also known as a null set. It follows that the universal set is the complement of the empty set.

Since the empty set has no elements while the universal set contains all elements, their complements are simply opposites of one another, as shown by the symbols‘ ∅’ = U and U’ = ∅

For example, set U = 1, 2, 3, 4, and 5 contains all of the items in set A, and set B contains all of the elements, therefore U’ = ∅(an empty set), and ∅’= 1, 2, 3, 4, and 5.

De Morgan’s Laws and Complements

Here are De Morgan’s laws on complementation.

For the intersection of two sets, their complement is the same as the complement of the sets. A’ U B’=(A ∩ B)’ (De Morgan’s Intersection Law).

Similarly, For the union of two sets, their complement is the complement of the intersection of the two sets. (A U B)’ = A’ ∩ B’ as per De Morgan’s Law of the union.

Using the aforementioned example to demonstrate De Morgan’s law, U ={ 9, 10, 11, 12, 13, 14, 15}, A =9, and B = {10, 11}. Thus, De Morgan’s Law of Union states that:

(A U B) = {9, 10, 11}

(A U B)’ = {12, 13, 14, 15} and A’ ∩ B’ = {12, 13, 14, 15}

To see how they are equal, notice that:

A’ = {10, 11, 12, 13, 14, 15 } and B’ = {9,12, 13, 14, 15}

So, we have:

(A U B)’ = A’ ∩ B’ = {12, 13, 14, 15}.

De Morgan’s Law of Intersection states that since:

(A ∩ B) = ∅ (empty)

(A ∩ B)’ = {9, 10, 11, 12, 13, 14, 15}

A’ U B’ = {9, 10, 11, 12, 13, 14, 15}

Where:

A’ = {9}, B’ = {10, 11} $\Rightarrow$ (A ∩ B)’ = A’ U B’

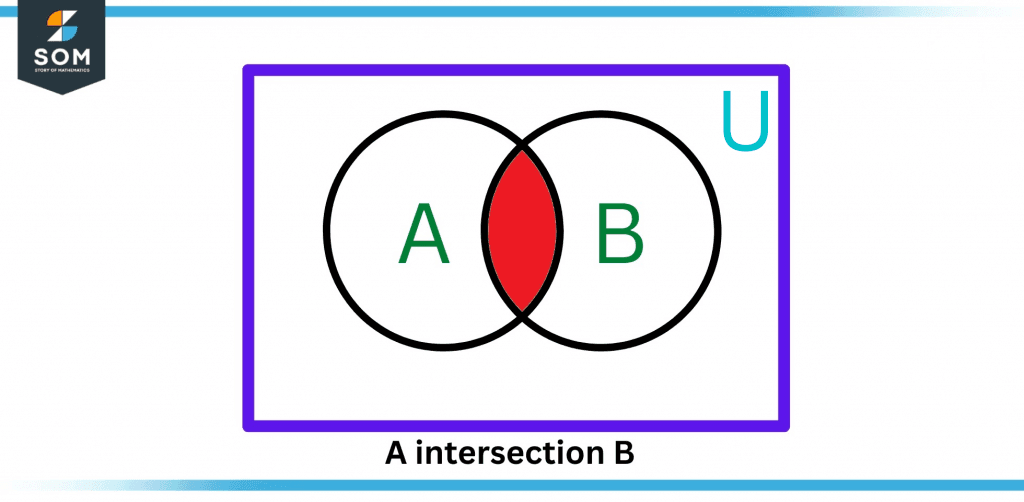
Figure 3 – A intersection B

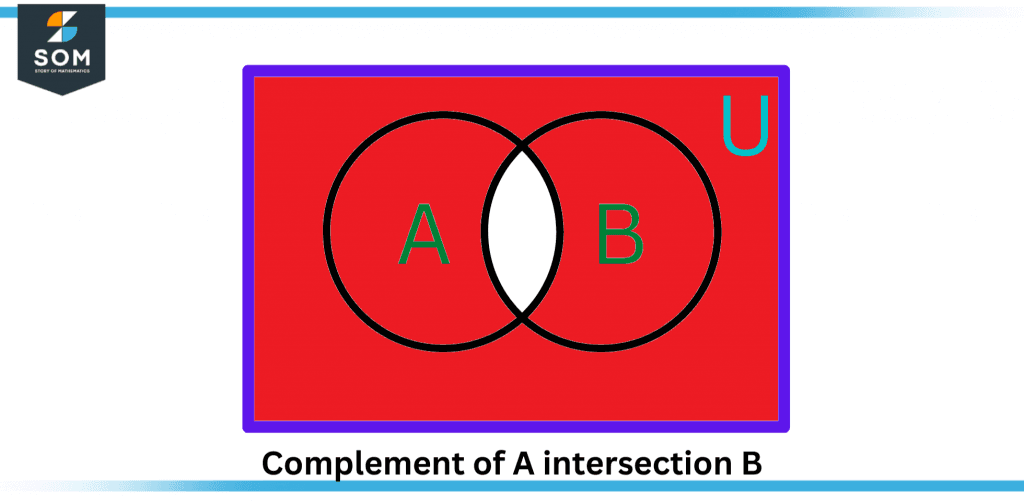
Figure 4 – Complement of A intersection B

Important Information Regarding Complement of a Set

• The empty set, often known as the null set, is the universal set’s complement.
• The components that both sets have in common are found in the intersection set.
• A set that includes every component of A, B, or both is said to be the union of two sets.

An Example of A Complement Set

Assume U is the universal set of class Z students, which consists of six students, and B is the set of all girls, which consists of thirty girls. Determine the complement of a set in terms of girls.

Solution

If set B is made up entirely of girls, then set B’s complement is made up entirely of guys. The complement of a set of girls is what separates the universal set from the set of all girls.

n(A’) is therefore 60 – 30 = 30. 30 girls make up the set’s complement as a result.

All images/mathematical drawings were created with GeoGebra.

Complement Probability Definition < Glossary Index > Complementary Angle Definition